Criptografía Cuántica - Principio y algoritmos

En general observar un sistema cuántico perturba al mismo, e impide que el observador conozca su estado exacto antes de la observación. Por lo tanto, si un sistema cuántico es utilizado para transferir información, alguien que quiera espiar la comunicación, o incluso el receptor previsto, podría verse impedido de obtener toda la información enviada por el emisor. Este rasgo negativo de la mecánica cuántica, conocido como principio de incertidumbre de Heisenberg, recientemente ha encontrado un uso positivo en el área de las comunicaciones privadas y seguras.

Principio básico de la criptografía cuántica

Como señalamos anteriormente, la criptografía cuántica se basa sobre el principio de incertidumbre de de Heisenberg. Veamos ahora como se puede aprovechar dicho principio para transmitir una clave en forma segura.

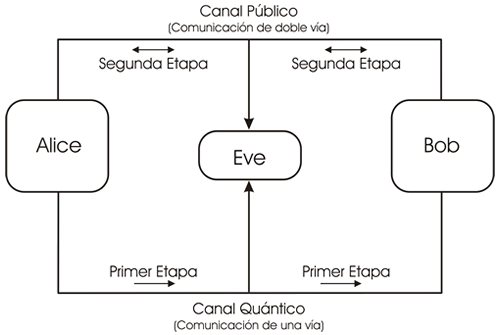
La criptografía cuántica hace uso de dos canales de comunicación entre los dos participantes. Un canal cuántico, el cual tiene un único sentido y que generalmente es una fibra óptica. El otro es un canal convencional, público y de dos vías, por ejemplo un sistema de comunicación por radio que puede ser escuchado por cualquiera que desee hacerlo.

Supongamos que Alice desea enviar una clave a Bob a través de un canal cuántico. El valor de cada bit es codificado dentro de una propiedad de un fotón, por ejemplo su polarización. La polarización de un fotón es la dirección de oscilación de su campo eléctrico. Esta polarización puede ser, por ejemplo, vertical, horizontal o diagonal (+45º y -45º).

Por ejemplo, Alice y Bob se ponen de acuerdo en que:

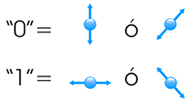
Un filtro puede ser utilizado para distinguir entre fotones verticales u horizontales. Otro filtro se utiliza para distinguir entre fotones diagonales (+45º y -45º).

Cuando un fotón pasa por el filtro correcto, su polarización no cambia. En cambio cuando un fotón pasa a través de un filtro incorrecto, su polarización es modificada en forma aleatoria.

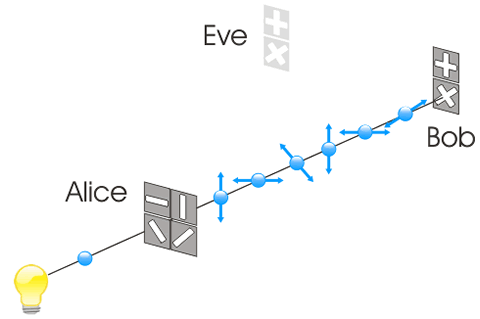
Por cada bit de la clave, Alice envía un fotón, cuya polarización es elegida de forma aleatoria. Las orientaciones seleccionadas son almacenadas por Alice.

Por cada fotón recibido, Bob elige de forma aleatoria cual filtro se va a utilizar y se registran el filtro seleccionado y el valor de la medición.

Una vez que se han intercambiado todos los fotones, Bob le revela a Alice a través de un canal convencional la secuencia de filtros que utilizo durante la transmisión de fotones. Luego Alice le dice a Bob en qué casos eligió el filtro correcto. En éste momento ambos saben en que casos sus bits deberían ser idénticos, es decir cuando Bob utilizo el filtro correcto. Estos bits formarán la clave final.

Si Eve intenta espiar la secuencia de fotones, al no conocer de antemano si la polarización del próximo fotón es diagonal o rectilínea, no podrá medirlo sin correr el riesgo de perturbarlo de tal forma que se introduzca un error.

Finalmente, Alice y Bob verifican el nivel de error de la clave final para validarla. Esto lo hacen haciendo públicos una cierta cantidad de bits. Si encuentran diferencias en sus bits, tienen una razón para sospechar que están siendo espiados y deberán descartar todos los datos y comenzar nuevamente el intercambio de fotones. Si coinciden y si se compararon una cantidad lo suficientemente grande de bits, pueden estar razonablemente seguros de que las partes que no han sido comparadas abiertamente en el canal inseguro son de hecho un secreto compartido y pueden conformar una clave secreta para ser utilizada en la transmisión de mensajes con significado. La transmisión de mensajes con significado se realiza sobre el canal publico o inseguro utilizando cualquier método de clave privada que crean conveniente por ejemplo DES (Data Encryption Standard), Triple DES o AES (Advanced Encryption Standard).

Por el momento no existe un sistema con el cual se puedan mantener comunicaciones por un canal cuántico. Por lo tanto la aplicación de la criptografía cuántica se ve restringida a la distribución de claves. Sin embargo, la transmisión olvidadiza puede ser utilizada como base para construir algoritmos de Zero Knowledge proofs y bit commitment.

El Algoritmo BB84

El esquema de codificación BB84 fue el primer codificador cuántico de información clásica en ser propuesto de forma tal que el receptor, legitimo o ilegitimo, pueda recuperar con 100% de confiabilidad. Esta es la base sobre la cual están fundados la mayoría de los protocolos cuánticos. El ejemplo que se vio anteriormente en la introducción a la criptografía cuántica se basa en este algoritmo.

1. La fuente de luz, generalmente un LED (Light emitting diode) o láser, es filtrada para producir un rayo polarizado en ráfagas cortas y con muy baja intensidad. La polarización en cada ráfaga es entonces modulado por el emisor (Alice) de forma aleatoria en uno de los cuatro estados (horizontal, vertical, circular-izquierdo o circular-derecho).
2. El receptor, Bob, mide las polarizaciones de los fotones en una secuencia de bases aleatoria (rectilíneo o circular).
3. Bob le dice públicamente al emisor que secuencia de bases utilizo.
4. Alice le dice al receptor públicamente cuales bases fueron elegidas correctamente.
5. Alice y Bob descartan todas las observaciones en las que no se eligió la base correcta.
6. Las observaciones son interpretadas usando un esquema binario por ejemplo: horizontal o circular-izquierdo es 0, vertical o circular-derecho es 1.

Este protocolo se complica con la presencia de ruido, el que puede ocurrir en forma aleatoria o ser introducido por una escucha. Con la existencia de ruido las polarizaciones observadas por el receptor pueden no coincidir con las emitidas por el emisor. Para lidiar con esta posibilidad, Alice y Bob deben asegurarse que poseen la misma cadena de bits. Esto se realiza usando una busqueda binaria con verificación de paridad para aislar las diferencias. Con el descarte del último bit de cada comparación, la discusión pública de la paridad se vuelve inofensiva. En el protocolo de Bennett de 1991 este proceso es:

1. Alice y Bob acuerdan una permutación aleatoria de las posiciones de los bits en sus cadenas, para distribuir aleatoriamente la posición de los errores.
2. Las cadenas se parten en bloques de longitud k, con k elegido de forma tal que la probabilidad de múltiples errores por bloque sea muy baja.
3. Por cada bloque, Alice y Bob computan y anuncian públicamente las paridades. Luego el último bit de cada bloque es descartado.
4. Para cada bloque en el que difirieron las paridades calculadas, Alice y Bob usan una búsqueda binaria con log(k) iteraciones para localizar y corregir el error en el bloque.
5. Para contemplar múltiples errores que aún no han sido detectados, los pasos 1 al 4 son repetidos con tamaños de bloque cada vez más grandes.
6. Para determinar si aun quedan errores, Alice y Bob repiten un chequeo aleatorio:

• Alice y Bob acuerdan públicamente una muestra de la mitad de las posiciones en sus cadenas de bits.
• Públicamente comparan las paridades y descartan un bit. Si las cadenas difieren, las paridades van a discrepar con probabilidad ½.
• Si hay discrepancias, Alice y Bob utilizan una búsqueda binaria para encontrarlas y eliminarlas.

7. Si no hay desacuerdos despues de l iteraciones, se concluye que sus cadenas coinciden con una probabilidad de error de 2^-l.

El protocolo BB84 fue publicado por Charles Bennett y Gilles Brassard en 1984.

Ejemplos del algoritmo BB84

Notación utilizada

Transmisión sin escuchas

Alice enviara una secuencia de 24 fotones.

La probabilidad de que el detector de Bob Falle es del 40%

Alice envía la siguiente secuencia de fotones:

Bob decide aleatoriamente si va a realizar una medición rectilínea o circular para cada fotón que Alice envié. La secuencia elegida es:

Por cada medición, existe una probabilidad del 0.4 (40%) de que el detector ni siquiera detecte el fotón. Los resultados de las mediciones son:

Luego, Bob le dice a Alice a través del canal público que tipo de mediciones (rectilínea o circular) ha logrado hacer exitosamente, pero no el valor de las mediciones.

Alice le dice a Bob, también por el canal público, cuales de las mediciones fueron del tipo correcto.

Como Bob solo va a hacer el mismo tipo de medición que Alice la mitad de las veces, y dado que la probabilidad de que el detector falle en leer un fotón es del 40%, se espera que unos 7.2 de los 24 dígitos compartidos sean utilizables. De hecho en éste ejemplo se generaron 8 dígitos utilizables.

En resumen:

Transmisión con escuchas

Alice enviara una secuencia de 24 fotones.

La probabilidad de que el detector de Bob Falle es del 40%.

Alice envía la siguiente secuencia de fotones:

Eve decide aleatoriamente si va a realizar una medición rectilínea o circular para cada fotón que Alice envié. La secuencia elegida es:

Por cada medición, existe una probabilidad del 0.4 (40%) de que el detector ni siquiera detecte el fotón. Los resultados de las mediciones de Eve son:

Bob decide aleatoriamente si va a realizar una medición rectilínea o circular para cada fotón que Alice envié. La secuencia elegida es:

Por cada medición, existe una probabilidad del 0.4 (40%) de que el detector ni siquiera detecte el fotón. Los resultados de las mediciones de Bob son:

Luego, Bob le dice a Alice a través del canal público que tipo de mediciones (rectilínea o circular) ha logrado hacer exitosamente, pero no el valor de las mediciones.

Alice le dice a Bob, también por el canal público, cuales de las mediciones fueron del tipo correcto.

Como Bob solo va a hacer el mismo tipo de medición que Alice la mitad de las veces, y dado que la probabilidad de que el detector falle en leer un fotón es del 40%, se espera que unos 7.2 de los 24 dígitos compartidos sean utilizables. De hecho en éste ejemplo se generaron 6 dígitos utilizables.

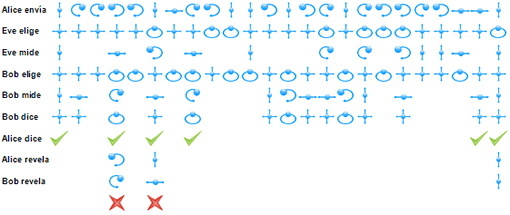
Bob y Alice quieren saber si alguien ha estado escuchando su comunicación, para lo cual comparten el 50% de los dígitos compartidos. Se va a seleccionar una muestra al azar para que ningún espía pueda predecir que dígitos van a ser verificados y evite modificarlos.

Alice revela primero el 50% de sus dígitos:

Bob le indica a Alice cual es el valor que midió para los mismos dígitos

Como 2 de los 3 dígitos verificados son incorrectos, Alice y Bob saben que alguien estuvo escuchando su intercambio de fotones.

En resumen:

Criptografia cuántica olvidadiza y transferencia comprometida

En un modelo de transmisión olvidadiza 1 de 2 (oblivious transfer, OT), una de las partes, Alice, tiene 2 bits b₀, b₁ los cuales envía a la otra parte, Bob, pero Bob solo puede obtener 1 de los 2 bits. Sin embargo, Alice no puede saber cual de los 2 bits es el que recibió Bob.

De forma análoga en un modelo de transmisión olvidadiza m de n, Alice envía n bits a Bob pero Bob solo puede obtener m de los n bits. Sin embargo, Alice no puede saber cuales son los m bits que recibió Bob.

Este tipo de transmisión puede ser utilizado como base para la construcción de otros protocolos criptográficos. Un ejemplo es la contracción de pruebas de cero-conocimiento (zero-knowledge proofs). Que son una forma de probar algo, por ejemplo que uno posee un permiso válido, sin revelar información adicional al receptor.

En una transferencia olvidadiza comprometida, (Committed Oblivious Transfer, cot), supongamos que Alice está comprometida a los bits y y Bob esta comprometido a luego de ejecutar cot (,)(), Bob va a estar comprometido a que = . Sin importar lo que haga, Alice no va a poder utilizar el protocolo para aprender información de , y Bob sin importar que haga no va a poder utilizar el protocolo para aprender información de .

Este tipo de transmisión permite que cada una de las partes involucradas en una transferencia olvidadiza esté segura que la otra parte esta realizando la operación de transferencia olvidadiza en las entradas declaradas.

Seguridad de la criptografía cuántica y de los métodos tradicionales

Primero estudiaremos la de seguridad de DES, AES y de RSA, los métodos criptográficos más utilizados. Ambos se basan en la suposición no probada de que no existe un algoritmo rápido para determinar la clave secreta. Por ejemplo, RSA se cree seguro por que aunque matemáticos de todo el mundo han trabajado arduamente, solo se han producido modestas mejoras en los algoritmos de factorización. Con lo cual con un pequeño incremento en los tamaños de las claves, RSA aún puede mantener la ventaja frente al crecimiento exponencial del poder de cómputo.

Tipos de Ataque

Pero esto está por cambiar, primero veamos los tres enfoques para atacar RSA hasta el momento.

Fuerza Bruta

Se intenta probar todas las posibles claves privadas. Este enfoque es poco práctico ya que requiere de un poder de cómputo extremadamente alto.

Ataques Matemáticos

Existen varios enfoques pero todos intentan producir el mi resultado, factorizar el producto de dos números primos.

Los tres enfoques matemáticos consisten en:

• Factorizar n en sus dos factores primos.
• Determinar Φ(n) directamente.
• Determinar d directamente sin calcular primero Φ(n).

El enfoque más importante es el primero, factorizar n en sus dos factores primos

Ataques no convencionales

Cuando uno creía que tenia un algoritmo criptográfico era razonablemente seguro, aparecen algoritmos sorprendentemente ingeniosos como el ataque de tiempo. Se ha demostrado que un espía puede determinar una clave privada con tan solo llevar un registro del tiempo le toma a una computadora descifrar mensajes. Los ataques de tiempo no solo se aplican a RSA sino también a otros algoritmos de clave pública. Este ataque es alarmante por que proviene de una dirección completamente inesperada.

Al ataque de tiempo hay que sumarle otros como el DPA (Differential Power Analysis) que consiste en analizar el consumo de energía u otros más recientes que indican que se puede distinguir diferentes patrones de la operación del CPU y de acceso a memoria mediante el sonido que se emite.

A estos ataques ingeniosos hay que sumarle los cambios que introducirán la mecánica cuántica y la computación cuántica. En 1994, Peter Shor de los laboratorios AT&T inventó un algoritmo cuántico capaz de factorizar números grandes. Más recientemente en 1996, Lov Grover de Lucent Technologies, los Laboratorios Bell, inventó un algoritmo de búsqueda cuántico. Este último puede utilizarse para acelerar radicalmente la búsqueda exhaustiva de claves en DES y AES.

Cuando se construya una computadora cuántica en un futuro no tan lejano, gran parte de la criptografía convencional caerá en pedazos. Y aunque falte una década hasta que las primeras computadoras cuánticas sean una realidad concreta, cierta información, como los diseños de armas nucleares, deberá seguir siendo secreta por lo que es importante que los mensajes que son enviados en forma secreta hoy continúen siendo secretos mañana.

Seguridad de la criptografía cuántica

A diferencia de los métodos convencionales que basan su seguridad en principios matemáticos, la criptografía cuántica se basa en principios físicos. Ya que por las leyes de la física cuántica es imposible medir un estado cuántico de un sistema sin alterarlo y según los físicos nunca va a ser posible. Se cree que la criptografía cuántica es un criptosistema indestructible. Incluso existen al menos dos estudios independientes que afirman haber probado su seguridad definitiva, es decir una prueba de que los protocolos criptográficos cuánticos son inmunes a todas las estrategias de escucha.

Sin embargo hay que reconocer el principal inconveniente de la criptografía cuántica, no brindar ningún mecanismo de autentificación. No hay forma de saber si Alice y Bob están realmente comunicándose entre ellos, y no con un intermediario (Eve) haciéndose pasar por ambos. Por lo tanto antes de que Alice y Bob puedan iniciar el protocolo cuántico, deberán intercambiar sus claves de autentificación.

Conclusión

La principal ventaja de la criptografía cuántica es que a diferencia que en todos los métodos de criptografía convencionales, la seguridad de la criptografía cuántica no depende de la capacidad de cómputo del adversario sino que está garantizada en forma absoluta por las leyes de la física cuántica. Otra gran ventaja que brinda es su capacidad única para detectar escuchas. Y aunque aún quede mucho por hacer en materia de investigación hasta que sea un método aplicable a gran escala, la criptografía cuántica es un salto importantísimo en materia de seguridad.

Bibliografía

Lomonaco, Samuel J. Jr. A Talk on Quantum Cryptography or How Alice Outwits Eve. 2001.

Stallings, William. Cryptography and Network Security: Principles and Practice. Prentice Hall, 1998.

A Quantum Leap for Cryptography. Genève, Id Quantique, 2003.

Chen, Zhide, and Hong Zhu. Quantum m-out-of-n Oblivious Transfer. 2003.

Ford, James. “Quantum Cryptography Tutorial” Dartmouth College. 1996.

Henle, Fred. “BB84 Demo.” Mercersburg Academy 28 October 2003. <http://monet.mercersburg.edu/henle/bb84/>

Crépeau, Claude, Jeroen van de Graaf, and Alain Tapp. Committed Oblivious Transfer And Private Multi-Party Computation. Université de Montréal, 1995.