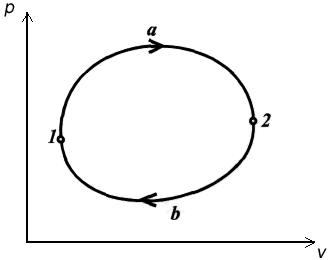
Acabamos de obtener la igualdad de Clausius para un ciclo reversible cualquiera. Si consideramos un ciclo formado por dos procesos reversibles, se cumplirá lo siguiente:
![]()
![]()
![]()
El resultado anterior demuestra que existe una cierta función S cuya variación en un proceso no depende del camino seguido, por lo tanto se trata de una función de estado. Clausius le dio a esta propiedad el nombre de entropía.
La formulación del segundo principio para procesos cíclicos reversibles queda de la siguiente manera utilizando esta nueva función de estado.
![]()
La entropía es una variable de estado extensiva, ya que se calcula a partir del calor intercambiado en un proceso. Podemos obtener la entropía específica sin más que dividir por la masa de nuestro sistema:
![]()
Las unidades de la entropía y de la entropía específica son, en el sistema internacional, (J/K) y (J/K kg) respectivamente.
Nos hemos referido hasta ahora al incremento en la entropía en un proceso cualquiera, y no a su valor absoluto. En principio se puede considerar el origen de la entropía como arbitrario, como se suele hacer en la práctica. En rigor, se puede demostrar que el cero de entropía coincide con el cero de la temperatura absoluta.
Variaciones de entropía en procesos reversibles
Partiendo de la definición de entropía y del primer principio podemos plantear el cálculo de las variaciones de entropía en procesos reversibles.
![]()
dqrev = du + δw = du + pdv
aplicando el 1er Principio
dqrev = dh – vdp
![]()
![]()
En el caso de que el sistema esté formado por gas ideal estas expresiones se pueden simplificar introduciendo la ecuación de estado.
du = cvdT dh = cpdT
![]()
![]()
![]()
![]()
En el caso de un sistema en cambio de fase, la variación de entropía se calcula teniendo en cuenta que el proceso se realiza a temperatura constante.
![]()
Donde r es el calor latente de cambio de fase.
Se puede decir en general que en un proceso reversible y adiabático la variación de entropía será nula. Se trata de un proceso isoentrópico.
![]()