Criptografía fractal

Aplicación de la teoría del caos a la criptografía

Un fractal es un objeto geométrico cuya estructura básica se repite en diferentes escalas. Los fractales son estructuras geométricas que combinan irregularidad y estructura. Los fractales están relacionados con la teoría del caos.

La criptografía fractal o caótica aplica fractales y sistemas caóticos para obtener métodos criptográficos.

Los casos de fractales que nos interesan para la criptografía son los generados por un proceso recursivo o iterativo basado en alguna función matemática.

Usando una función caótica pare encriptar

Una de las características de la dinámica caótica es su sensibilidad extrema a las condiciones iniciales, por ejemplo dos valores iniciales relativamente cercanos van a discrepar a medida que el sistema evolucione. Como veremos es posible utilizar una función caótica que es inicializada con una clave para encriptar datos.

La seguridad de este tipo de criptosistema se basa en la esperanza de que sin conocer la clave secreta, el comportamiento caótico sea lo suficientemente difícil de predecir utilizando métodos analíticos. Esto reduciría los posibles ataques a una sola categoría, los ataques de fuerza, en los cuales se prueban todas las claves posibles contra los datos encriptados. Los ataques de fuerza rara vez son exitosos ya que dependen directamente de la longitud de la clave utilizada. Para una clave de n bits pueden existir 2ⁿ posibilidades, y el uso de claves de 256 bits o más, provee tal protección que el solo hecho de contar hasta esos valores requeriría un enorme consumo de energía.

Para ilustrar las posibilidades de la aplicación de funciones caóticas en la criptografía se tomara como ejemplo el conocido mapa logístico:

Cuando r = 3.9, el mapa logístico exhibe un comportamiento caótico, y por lo tanto la propiedad de sensibilidad a las condiciones iniciales.

x₀ será el valor de la condición inicial, y con la fórmula sacamos el x₁ que pasa a ser usado como el x₀ del nuevo cálculo,y así sucesivamente en forma recursiva.

Un cifrador por bloques simple

Como ejemplo se explicara un simple algoritmo que utiliza como base el mapa logístico. Este es un algoritmo de cifrado por bloques con una clave secreta. La clave es utilizada para generar un pad que luego es combinado con el texto en claro por bloques de 8 bits.

En este cifrador, las claves de sesión forman parte de la clave de encriptación y se toman en forma cíclica. Por ejemplo si se utiliza una clave de 256 bits, las claves de sesión irán desde la k₁ a la k₂₅₆.

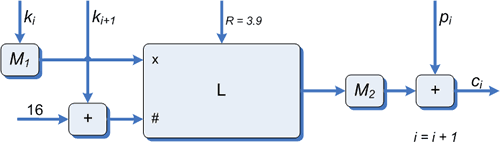
El modo en que se genera el pad consiste en tomar dos claves de sesión sucesivas k_i y k_i+1 y en lugar de combinarlas directamente con el texto en claro, se utilizan como condiciones iniciales para el mapa caótico.

El bloque M₁ representa un mapeo del espacio de claves de sesión, todos los enteros entre el 0 y 255, en el dominio del mapa logístico L, todos los reales en el intervalo [0,1]. La suma de la siguiente clave de sesión y el número 16 es usada como el número de iteraciones del mapa logistico. M₂ usa un subconjunto difuso [1] para mapear el dominio del mapa logístico, reales entre 0 y 1, nuevamente al intervalo discreto [0,255]. A medida que se encripta un nuevo bloque, el contador i usado para llevar un registro de la clave de sesión actual es incrementado. La salida del mapa logístico es combinada con el texto en claro para dar el texto encriptado.

[1] Un subconjunto difuso, es un conjunto que puede contener elementos de forma parcial, es decir que la propiedad x ∈ A puede ser cierta, falsa o solamente posible.

El proceso de desencriptado es simple, el mismo pad es generado a partir de la clave y se utiliza para descombinarlo del texto encriptado para recuperar el texto en claro.

En un análisis sencillo de este cifrador se ve que posee buenas propiedades estadísticas. Sin embargo por más que estadísticamente luce bien, haciendo una comparación gráfica tomando como texto claro una imagen y comparándola imagen sin encriptar con su contraparte encriptada se puede observar que gran cantidad de la información de la imagen original es visible en la imagen cifrada. Este problema ocurre por que el pad producido por el cifrador depende solo de la clave y por lo tanto pose un periodo del tamaño de la clave. Esto significa que series del mismo pad son utilizadas en forma repetida dando lugar a patrones de posicionamiento. Los patrones son fácilmente reconocidos por el ojo humano y aunque los colores hayan cambiado, aun es posible distinguir de qué se trata la imagen original.

Imagen Original	Imagen Encriptada

El comportamiento periódico del cifrador es un indicio de que el mismo no es seguro. Un método que se puede utilizar para resolver este problema es agregando retroalimentación al mecanismo del cifrador. De esta forma la encriptación no solo dependerá de la clave sino que también dependerá del texto en claro encriptado previamente.

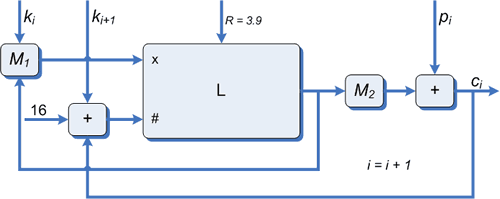
Por ejemplo una forma de retroalimentación es utilizar la salida de la función caótica ya añadirla a la entrada para obtener el nuevo x. Además el valor numérico del bloque anterior es añadido al número de iteraciones.

Estas modificaciones hacen que el cifrador funcione mucho mejor que antes y que el fantasma de la imagen original que podía apreciarse en la imagen encriptada prácticamente desaparezca.

 

Imagen Original	Imagen Encriptada Sin retroalimentación	Imagen Encriptada Con Retroalimentación