Otro ejemplo de sistema caótico que puede se ha aplicado a la criptografía es el problema de n cuerpos El problema de n cuerpos intenta determinar el movimiento de varias partículas en presencia de fuerzas fuertemente atractivas (tales como fuerza gravitacional y fuerza electromagnética).
Cualquier partícula que tenga masa obedece la ley de gravitación del Newton (al menos en escala macroscópica). Esta ley establece que la fuerza de atracción entre dos cuerpos es proporcional al producto de sus masas, e inversamente proporcional al cuadrado de la distancia entre sus centros, dando:
![]()
Donde G es la constante de proporcionalidad (constante gravitatoria universal)
Al observar un objeto particular, la magnitud de su vector de aceleración puede ser determinada dividiendo la masa, lo que deja a esta magnitud en función de la masa del otro objeto, y de la distancia entre ellas. La aceleración, sin embargo, es la segunda derivada de la posición de un objeto con respecto a tiempo, por lo tanto que la ecuación resultante es:
![]()
donde P es la posición del objeto en función de tiempo.
Podemos ahora ver eso en un espacio de n-dimensiones, basándose en la fórmula euclidiana de la distancia, para cada coordenada de la aceleración de una partícula se puede demostrar que tiene la forma:
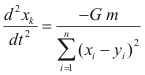
donde los valores de x son las coordenadas del objeto que es observado, y los valores los valores de y son las coordenadas del objeto hacia el cual se está moviendo.
Las ecuaciones diferenciales de segundo orden de esta forma se pueden solucionar en forma cerrada, pero como a medida que se agregan más objetos que influyen el que estamos observando, la situación se hace mucho más compleja, y no es posible solucionar exactamente la ecuación. La ecuación resultante es de la forma:
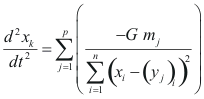
donde p es el número de objetos en el sistema que actúan sobre el objeto que estamos observando.
El problema de n cuerpos se ocupa de determinar el movimiento de partículas que están actuando bajo la influencia de campos radiales proyectados de fuentes puntuales.
Para el caso particular del problema de 2 cuerpos (y el caso trivial del problema de 1 cuerpo), las ecuaciones diferenciales tienen son solubles. Cuando el problema se generaliza a tres o más cuerpos, llega a ser imposible (a excepción de casos especiales) encontrar soluciones de forma cerrada a las ecuaciones diferenciales que definen el movimiento del sistema. Por lo tanto es imposible determinarse exactamente donde estará un cuerpo dado después de un período de tiempo finito. Es, sin embargo, posible utilizar las ecuaciones diferenciales que definen al sistema para aproximar las posiciones de las partículas mediante iteración sobre un pequeño intervalo de tiempo.
Se han hecho estudios de criptosistemas en los que se aplican los principios del problema de n cuerpos mencionados anteriormente. El algoritmo utiliza una serie de funciones singulares simples que funcionan directamente sobre los datos binarios para hacerlo teóricamente impredecible.
La complejidad para romper este sistema yace en la dificultad de encontrar un conjunto de fuerzas de atracción que causarían una trayectoria dada a una partícula. Para una única trayectoria (como se define dentro de la precisión de la capacidad de computo de las computadoras) no habrá soluciones únicas, y por lo tanto será difícil que un atacante determine la solución correcta (la clave y el correspondiente del texto en claro).
Ejemplo de un algoritmo que emplea un sistema caótico
Definiciones
A: Un sistema caótico (por ejemplo el sistema de n cuerpos)
P: Un conjunto de parámetros de tamaño n. (por ejemplo la ubicación de todos los objetos de masas iguales). P también es la clave.
Un conjunto de n funciones reversibles F[k] y sus respectivas funciones inversas ~F[k]
Algoritmo de encriptación
Ingresar P en el sistema A
Numerar en forma secuencial todos los puntos P
Repetir mientras haya datos sin encriptar
Convertir un bloque de tados en un punto R
Ingresar R en el sistema caótico
Determinar el punto P al cual el punto R será atraído y llamarlo K
Crear un bloque de texto cifrado compuesto de K
Agregar al bloque cifrado F[k](R)
Fin del ciclo
¿Por qué es segura la criptografía caótica?
Los mapas caóticos han sido y se continúan utilizando para generar secuencias de números pseudo-random, que se pueden utilizar como pad para los mensajes que desean cifrar.
Los mapas discretos producen ciclos que son imprevisibles y a menudo cortos.
Las matemáticas del caos por si mismas son complejas. El cómputo de ecuaciones no lineales mediante los sistemas lineares aumenta esta complejidad.
En el ejemplo de la encriptación utilizando un sistema caótico, se tiene como ventaja el hecho de que se ha probado que las ecuaciones diferenciales involucradas en el problema de n-cuerpos no poseen una solución cerrada.
Desventajas de la criptografía caótica
Es un hecho bien conocido de la dinámica simbólica que cuando una órbita caótica se convierte a una secuencia de símbolos (conjuntos de alguna partición) puede llegar a ser posible calcular la condición inicial con una exactitud mucho mayor que el tamaño de los conjuntos de la partición.
El hecho que este método se base en aritmética de punto flotante constituye una posible desventaja puesto que esto lo hace dependiente de la máquina, y se deben tomar precauciones al implementar los esquemas en un software.
Una de las principales desventajas de estos métodos es el tiempo. Las iteraciones toman mucho tiempo de cómputo y por ello no se puede implementar este tipo de cifradores para flujo de datos.
Conclusiones
En el campo de la criptografía se están buscando continuamente nuevos métodos para garantizar la seguridad de los datos. La aplicación de sistemas caóticos a la misma no es una idea nueva pero recientemente ha tomado nuevo impulso.
En el ejemplo del criptosistema que aplica el problema de n-cuerpos, hasta el momento no se ha encontrado otra forma de ataque que no sea un ataque de fuerza. Esto es un indicio de que posiblemente este sea un criptosistema excepcionalmente seguro.
La principal desventaja de todos los métodos desarrollados hasta el momento es que son computacionalmente muy costosos, ya que los mismos implican ciclos y operaciones de punto flotante. Los métodos criptográficos tradicionales como el DES son, en términos de recursos de computo, mucho más eficientes. Sin embargo con el avance del poder de cálculo de los nuevos procesadores y la promesa de mejor seguridad la criptografía caótica tiene asegurado su lugar en el futuro.
Bibliografía
Stallings, William. Cryptography and Network Security: Principles and Practice. Prentice Hall, 1998.
Whitehead, Nick: Overton, Michael; LaBry, Zach; Hamilton, Franklin; Leising, Brian. Encrypting Chaos: Fractal Encryption. 2003
Roskin, K.M.; Casper J.B. From Chaos to Cryptography. 1999
Gallagher, Jonathan B.; Goldstein, Jeremy. Sensitive Dependence Cryptography. 1996