La idea central que subyace en la descripción de la estructura electrónica de los sólidos metálicos es la de que los electrones de valencia de cada átomo se distribuyen a través de toda la estructura. Este concepto se expresa, de una manera más formal, haciendo una simple extensión de la Teoría de Orbitales Moleculares, en la que el sólido se trata como molécula infinitamente larga. Estos principios pueden también aplicarse a la descripción de sólidos no metálicos como los sólidos iónicos o los sólidos moleculares.
Formación de la banda mediante el solapamiento orbital.
El solapamiento de un gran número de orbitales atómicos conduce a un conjunto de orbitales moleculares que se encuentran muy próximos en energías y que forman virtualmente lo que se conoce como una banda. Las bandas se encuentran separadas entre sí mediante espacios energéticos a los que no les corresponde ningún orbital molecular (Figura 2).
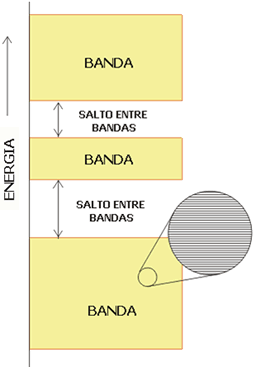
Figura 2. La estructura electrónica de un sólido se caracteriza por la existencia de bandas de orbitales.
Para poder visualizar la formación de una banda considérese una distribución lineal de átomos (sólido unidimensional), separados todos a la misma distancia (a), en los que cada átomo posee un orbital de tipo s. Cada orbital de tipo s de un átomo solapará con el orbital s del átomo vecino. Así, si sólo hubiera dos átomos en el conjunto el solapamiento conduciría a la formación de 2 orbitales moleculares, uno de enlace y otro de antienlace. Si tenemos 3 átomos, el solapamiento de los 3 orbitales de tipo s originaría la formación de 3 orbitales moleculares, de enlace, de no enlace y de antienlace. A medida que se van añadiendo átomos al conjunto cada uno contribuye con su orbital molecular al solapamiento y en consecuencia se obtiene un nuevo orbital molecular. Así, cuando el conjunto está formado por N átomos se obtienen N orbitales moleculares. El orbital molecular de menor energía no presenta ningún nodo entre los átomos vecinos, mientras que el orbital molecular de mayor energía presenta un nodo entre cada par de átomos vecinos.
![]()
Los restantes orbitales van teniendo sucesivamente 1, 2, 3... nodos internucleares y sus energías están comprendidas entre la del orbital más enlazante (de menor energía) y la del más antienlazante (mayor energía). La diferencia de energía entre los N orbitales moleculares es tan pequeña que se forma una banda o continuo de niveles de energía. La anchura total de la banda depende de la fuerza de la interacción entre los orbitales atómicos de los átomos vecinos, de forma que, cuanto mayor sea la interacción, mayor será el solapamiento entre los orbitales y mayor será la anchura de la banda resultante (o separación entre el orbital molecular más enlazante y el más antienlazante). La anchura de una banda es, por lo general, una medida del grado de localización del enlace. Una banda estrecha representa un alto grado de localización de un enlace y a medida que se va haciendo más ancha los enlaces se hacen más deslocalizados.
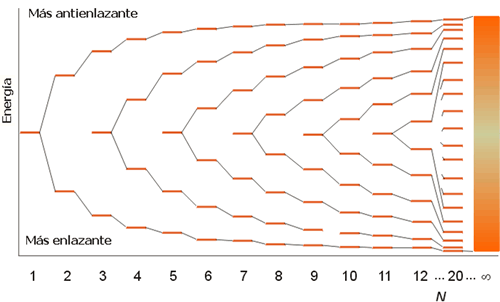
Figura 3. Formación de una banda de orbitales moleculares.
La banda que se ha descrito se ha formado a partir del solapamiento de orbitales s y se denomina, por tanto, banda s (Figura 4). Si en los átomos existen orbitales de tipo p disponibles, éstos pueden solapar originando una banda p (Figura 5). Como los orbitales p poseen mayor energía que los orbitales s de la misma capa, se observa a menudo la separación entre la banda s y la banda p. Pero si las bandas son anchas y las energías de los orbitales s y p de la misma capa no difieren mucho entonces ambas bandas se solapan (Figura 6). Este solapamiento es el responsable de que los elementos del grupo 2 de la Tabla Periódica tengan un comportamiento metálico. De la misma forma, la banda d está formada por el solapamiento de orbitales atómicos d.
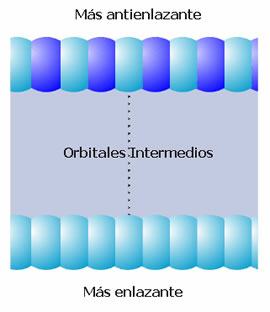
Figura 4. Orbitales moleculares y banda s.
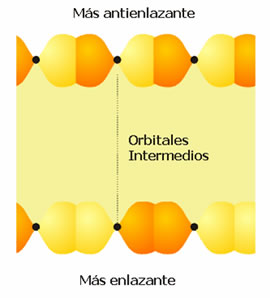
Figura 5. Orbitales moleculares y banda p.
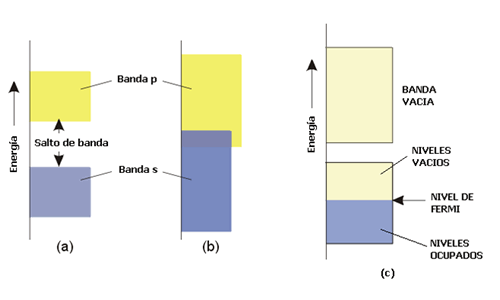
Figura 6. (a) y (b) Bandas s y p, que pueden solapar o no, dependiendo de la anchura. (c) Niveles ocupados y nivel de Fermi a o K.
El nivel de Fermi
A la temperatura T = 0 K los electrones ocupan los orbitales moleculares que forman la banda siguiendo el principio de construcción citado en la lección 2. Si cada átomo del modelo (distribución lineal de átomos) contribuye a la banda s con 1 electrón entonces, a T = 0 K la mitad de los orbitales que forman la banda (1/2 N) estarán ocupados. El orbital molecular de mayor energía que se encuentra ocupado se conoce como el nivel de Fermi y, en este caso, estará situado en el centro de la banda. La banda de menor energía que se encuentra ocupada o semiocupada se conoce como banda de valencia. La banda de menor energía que se encuentra vacía se conoce como la banda de conducción.
A una temperatura superior a 0 K, la población de los orbitales moleculares que forman la banda, P, viene dada por la distribución de Fermi-Dirac, que es una versión de la distribución de Boltzmann, y que tiene en cuenta que cada nivel de energía de la banda sólo puede estar ocupado por 2 electrones como máximo. Esta distribución P tiene la siguiente forma:
P = 1/(e(E-μ)/kT + 1)
donde μ es el potencial químico o energía del nivel para el cual P = 1/2. La forma de la distribución de Fermi-Dirac se muestra en la Figura 7. Cuando la banda no está completamente ocupada los electrones que se encuentran próximos al nivel de Fermi pueden, fácilmente, promocionarse a niveles vacíos que se encuentran inmediatamente por encima de éste. Como resultado, los electrones gozan de movilidad y pueden moverse libremente a través del sólido. Este fenómeno origina que la sustancia sea un buen conductor eléctrico. Como se ha visto, en un metal la conductividad eléctrica disminuye con la temperatura; este hecho se debe a las interferencias (los electrones se pueden describir como ondas) que se producen entre los electrones que se mueven por el sólido y las vibraciones de la red cristalinas, provocadas por el movimiento de los átomos, vibraciones que aumentan al hacerlo la temperatura.
La densidad de estados.
El número de niveles de energía con un determinado valor de energía se conoce como la densidad de estados, N(E) o ρ. Es posible representar la variación de energía de una banda en función de la densidad de estados, tal como aparece en la Figura 8 para las bandas s y p. La densidad de estados no es uniforme a lo largo de toda la banda debido a que los niveles de energía se empaquetan más a unos determinados valores de energía que a otros. Este hecho produce que la banda s, por ejemplo, presente la mayor densidad de estados en el centro y la menor densidad de estados en los extremos de la banda. La razón de este comportamiento está en la forma de las combinaciones lineales que originan los orbitales moleculares que constituyen la banda s. Existe una única combinación lineal que conduce al orbital molecular más enlazante (el límite inferior de la banda)y otra que conduce al más antienlazante (el límite energético superior de la banda). Sin embargo hay varias combinaciones posibles, degeneradas en energía, que dan lugar a los orbitales moleculares que forman la parte central de la banda s.
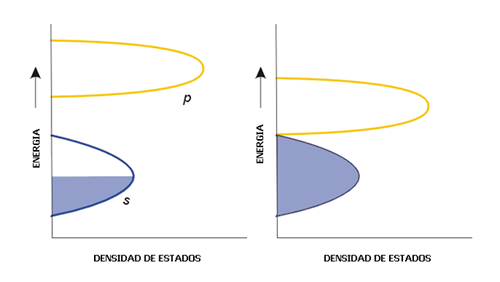
Figura 8. Densidad de estados típica de un metal (izquierda) y de un semimetal (derecha).
Entre dos bandas separadas por un espaciamiento energético, la densidad de estados en el mismo es cero, pues no hay niveles energéticos en dicha separación. En algunos casos especiales puede ocurrir que la separación entre la banda de valencia y la de conducción sea nula, aunque la densidad de estados en el punto de conjunción de ambas bandas sea cero. Esta es la estructura de bandas típica de un semimetal. Sólo algunos electrones pueden pasar de la banda llena a la banda vacía de forma que estos materiales poseen conductividades eléctricas bajas. Un ejemplo importante de semimetal es el grafito.