Teoría de la Información

Hace ya mucho tiempo que la información es almacenada en forma digital, sin embargo hubo un periodo durante el cual las computadoras eran una novedad, y donde los únicos medios de almacenamiento conocidos eran los libros. Es en ese marco que un matemático francés: Claude Shannon se dedicó a elaborar una teoría sobre como tratar a la información almacenada en forma digital. Sobre eso trata esta texto y esa es la razón por la cual la primera parte esta destinada a entender los fundamentos básicos de la Teoría de la Información.

Existen muchas definiciones de 'información'. Dependiendo del autor o del contexto en el cual se discuta el tema podemos encontrar aproximaciones de lo más variadas. En este apunte trabajaremos con información que se almacena en computadoras. Una computadora en su nivel mas bajo conoce solamente dos símbolos (por ahora): el cero y el uno, pues funciona en base a circuitos electrónicos que utilizan elementos bi-estables; en este texto trataremos sobre problemas relacionados con el almacenamiento de información en computadoras digitales, estudiaremos técnicas de compresión de datos para lograr almacenar mensajes utilizando la menor cantidad de bits posibles, observaremos técnicas de encriptación para ocultar la información almacenada de miradas indiscretas y desarrollaremos técnicas de autocorrección para proteger a la información almacenada frente a posibles fallas (ninguna computadora está garantizada contra fallas, la suya tampoco).

Nos basaremos en este apunte en la denominada 'teoría de la información' elaborada por Shannon en 1948 y que ha cobrado mucha vigencia con el advenimiento de la era de las computadoras digitales. Para comenzar debemos partir de algunas definiciones sobre la nomenclatura a utilizar, nomenclatura basada en la teoría de la información de Shannon.

FUENTE

Una fuente es todo aquello que emite mensajes. Por ejemplo, una fuente puede ser una computadora y mensajes sus archivos, una fuente puede ser un dispositivo de transmisión de datos y mensajes los datos enviados, etc. Una fuente es en sí misma un conjunto finito de mensajes: todos los posibles mensajes que puede emitir dicha fuente. En compresión de datos tomaremos como fuente al archivo a comprimir y como mensajes a los caracteres que conforman dicho archivo.

MENSAJE

Un mensaje es un conjunto de ceros y unos. Un archivo, un paquete de datos que viaja por una red y cualquier cosa que tenga una representación binaria puede considerarse un mensaje. El concepto de mensaje se aplica también a alfabetos de mas de dos símbolos, pero debido a que tratamos con información digital nos referiremos casi siempre a mensajes binarios.

CÓDIGO

Un código es un conjunto de unos y ceros que se usan para representar a un cierto mensaje de acuerdo a reglas o convenciones preestablecidas. Por ejemplo al mensaje 0010 lo podemos representar con el código 1101 usando para codificar la función (NOT). La forma en la cual codificamos es arbitraria.

Un mensaje puede, en algunos casos representarse con un código de menor longitud que el mensaje original. Supongamos que a cualquier mensaje S lo codificamos usando un cierto algoritmo de forma tal que cada S es codificado en L(S) bits, definimos entonces a la información contenida en el mensaje S como la cantidad mínima de bits necesarios para codificar un mensaje.

INFORMACIÓN

La información contenida en un mensaje es proporcional a la cantidad de bits que se requieren como mínimo para representar al mensaje.

El concepto de información puede entenderse mas fácilmente si consideramos un ejemplo.
Supongamos que estamos leyendo un mensaje y hemos leído "string of ch", la probabilidad de que el mensaje continúe con "aracters" es muy alta por lo tanto cuando realmente leemos "aracters" del archivo la cantidad de información que recibimos es muy baja pues estabamos en condiciones de predecir que era lo que iba a ocurrir. La ocurrencia de mensajes de alta probabilidad de aparición aporta menos información que la ocurrencia de mensajes menos probables. Si luego de "string of ch" leemos "imichurri" la cantidad de información que recibimos es mucho mayor.

Clasificación de Fuentes:

Por la naturaleza generativa de sus mensajes una fuente puede ser aleatoria o determinística.

Por la relación entre los mensajes emitidos una fuente puede ser estructurada o no estructurada ( o caótica).

Existen varios tipos de fuentes. Para la teoría de la información interesan las fuentes aleatorias y estructuradas. Una fuente es aleatoria cuando no es posible predecir cual es el próximo mensaje a emitir por la misma. Una fuente es estructurada cuando posee un cierto nivel de redundancia, una fuente no estructurada o de información pura es aquella en que todos los mensajes son absolutamente aleatorios sin relación alguna ni sentido aparente, este tipo de fuente emite mensajes que no se pueden comprimir, un mensaje para poder ser comprimido debe poseer un cierto nivel de redundancia, la información pura no puede ser comprimida pues perderíamos un grado de conocimiento sobre el mensaje.

Ejemplos:

Fuente Estructurada.	Fuente no-estructurada.

Distintos tipo de códigos, Códigos decodificables

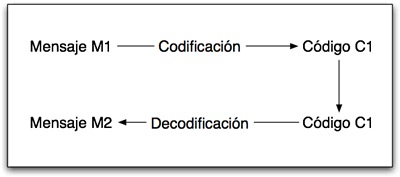
Como vimos, un código es una representación binaria de un cierto mensaje, el proceso de codificación y decodificación es simple e intuitivo, el codificador recibe un mensaje "m1" y emite un código, el decodificador recibe un código y emite un mensaje "m2", considerando que nuestros codificadores pretenderán no perder información debemos pedir que m1 sea igual a m2, es decir que el código es decodificable.

Un código es decodificable sí y solo sí un código solo puede corresponder a un único mensaje.

Ejemplo:
Sea el siguiente esquema de codificación:

a=0
b=01
c=10

Si el decodificador recibe el código: "0010" no puede distinguir si el mensaje original fue "aba" o "aac", ya que puede interpretarlo como 0 01 0 o como 0 0 10

Este tipo de código no-decodificable se denomina "libre de prefijo", para construir códigos libres de prefijo para un alfabeto puede usarse casi cualquier función, aunque todo el proceso de codificación en sí deja de tener sentido pues no es posible decodificar correctamente los mensajes.

Ejemplo 2:
Sea el siguiente esquema:

a=0
b=01
c=11

El código "00111" solo puede corresponder a "abc" (intente decodificarlo de otra forma!) sin embargo el decodificador es incapaz de deducir esto a medida que va leyendo los códigos, necesita saber cuales van a ser los próximos bits para poder interpretar los anteriores, este tipo de código no se considera decodificable (aunque lo sea) y también tendremos que evitarlo.

Códigos prefijos

Los códigos prefijos son códigos decodificables, cada código se puede reconocer por poseer un prefijo que es único al código, el prefijo de un código no puede ser igual a un código ya existente.

Ejemplo:

a=0
b=10
c=11

Es un código prefijo, notar que si agregamos mas códigos estos no pueden comenzar con "0" ni "10" ni "11" pues el decodificador los confundiría con "a" "b" o "c", en consecuencia a este código no podríamos agregarle nuevos códigos.

Entropía de una fuente

Ya hablamos del concepto de información, veremos ahora como se mide la misma . De acuerdo a la teoría de la información, el nivel de información de una fuente se puede medir según la entropía de la misma. Los estudios sobre la entropía son de suma importancia en la teoría de la información y se deben principalmente a Shannon, existen a su vez un gran numero de propiedades respecto de la entropía de variables aleatorias debidas a Kolmogorov.

Dada una fuente "F" que emite mensajes, resulta frecuente observar que los mensajes emitidos no resulten equiprobables sino que tienen una cierta probabilidad de ocurrencia dependiendo del mensaje. Para codificar los mensajes de una fuente intentaremos pues utilizar menor cantidad de bits para los mensajes más probables y mayor cantidad de bits para los mensajes menos probables de forma tal que el promedio de bits utilizados para codificar los mensajes sea menor a la cantidad de bits promedio de los mensajes originales. Esta es la base de la compresión de datos.

A este tipo de fuente se la denomina fuente de orden-0 pues la probabilidad de ocurrencia de un mensaje no depende de los mensajes anteriores, a las fuentes de orden superior se las puede representar mediante una fuente de orden-0 utilizando técnicas de modelización apropiadas.

Definimos a la probabilidad de ocurrencia de un mensaje en una fuente como la cantidad de apariciones de dicho mensaje dividido el total de mensajes.

Supongamos que Pi (P sub i) es la probabilidad de ocurrencia del mensaje-i de una fuente, y supongamos que Li es la longitud del código utilizado para representar a dicho mensaje, la longitud promedio de todos los mensajes codificados de la fuente se puede obtener como:

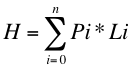
Promedio ponderado de las longitudes de los códigos de acuerdo a sus probabilidades de ocurrencia, al número "H" se lo denomina "Entropía de la fuente" y tiene gran importancia. La entropía de la fuente determina el nivel de compresión que podemos obtener como máximo para un conjunto de datos, si consideramos como fuente a un archivo y obtenemos las probabilidades de ocurrencia de cada caracter en el archivo podremos calcular la longitud promedio del archivo comprimido, se demuestra que no es posible comprimir estadísticamente un mensaje/archivo mas allá de su entropía. Lo cual implica que considerando únicamente la frecuencia de aparición de cada caracter la entropía de la fuente nos da el límite teórico de compresión, mediante otras técnicas no-estadísticas puede, tal vez, superarse este límite.

El objetivo de la compresión de datos es encontrar los Li que minimizan a "H", además los Li se deben determinar en función de los Pi, pues la longitud de los códigos debe depender de la probabilidad de ocurrencia de los mismos (los mas ocurrentes queremos codificarlos en menos bits).

Se plantea pues:

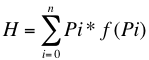(Minimizar)

A partir de aquí y tras intrincados procedimientos matemáticos que fueron demostrados por Shannon oportunamente se llega a que H es mínimo cuando f(Pi) = log2 (1/Pi).

Entonces:

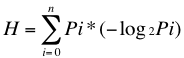
La longitud mínima con la cual puede codificarse un mensaje puede calcularse como Li=log2(1/Pi) = -log2(Pi). Esto da una idea de la longitud a emplear en los códigos a usar para los caracteres de un archivo en función de su probabilidad de ocurrencia.

Reemplazando Li podemos escribir a H como:

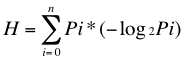(Repetido por Conveniencia)

De aquí se deduce que la entropía de la fuente depende únicamente de la probabilidad de ocurrencia de cada mensaje de la misma, por ello la importancia de los compresores estadísticos (aquellos que se basan en la probabilidad de ocurrencia de cada caracter). Shannon demostró, oportunamente que no es posible comprimir una fuente estadísticamente mas allá del nivel indicado por su entropía.

Un mundo de 8 bits

Como sabemos un archivo en una computadora es una secuencia de BITS, sin embargo en nuestras definiciones de entropía y longitud ideal de los caracteres estamos considerando la probabilidad de ocurrencia de caracteres es decir bloques de 8 bits, podríamos pensar si los resultados cambiarían considerando bytes de 9 o 7 bits, por ejemplo. La respuesta es afirmativa, pero la entropía tendería a aumentar a medida que nos alejamos del valor de 8 bits por byte. El motivo por el cual ocurre esto reside en que en cualquier archivo almacenado en una computadora los elementos que pueden ser dependientes unos de otros son los bytes y no los bits, esto hace a la estructura de la fuente, concepto del cual hemos hablado. A medida que nos alejamos del valor de 8 bits para nuestro concepto de byte perdemos estructura en nuestra fuente y la misma cada vez se vuelve mas aleatoria por lo que podremos comprimirla en menor medida. De aquí surge que tomemos siempre bytes de 8 bits, tarea que puede sonar obvia pero que merece mas de una reflexión.

Ejemplo:

Sea el siguiente string/archivo/fuente:

"Holasaludosatodos" (17 bytes)

Tenemos la siguiente tabla:

Carácter	Frecuencia	Probabilidad	Longitud Ideal
H	1	1/17=0.0588	-log2(0.0588)=4.0874 bits
o	4	4/17=0.2353	-log2(0.2353)=2.0874 bits
l	2	2/17=0.1176	-log2(0.1176)=3.0874 bits.
a	3	3/17=0.1765	-log2(0.1765)=2.5025 bits
s	3	3/17=0.1765	-log2(0.1765)=2.5025 bits
u	1	1/17=0.0588	-log2(0.0588)=4.0874 bits
d	2	2/17=0.1176	-log2(0.1176)=3.0874 bits
t	1	1/17=0.0588	-log2(0.0588)=4.0874 bits

H = 3 * 0.0588 * 4.0874 + 0.2353 * 2.0874 + 2 * 0.1176 * 3.0874 + 2 * 0.1765 * 2.5025

H = 2.82176233222 bits x byte.

H * 17 = 47.96 bits.

El string en cuestión no puede ser comprimido en menos de 47.96 bits, es decir unos 6 bytes. Este es el límite teórico e ideal al cual puede comprimirse nuestra fuente.

La desigualdad de Kraft

Sea el alfabeto A={a0,a1,...,an-1} la cantidad de símbolos de "A" es |A|=N.

Supongamos que Cn es el código libre de prefijo correspondiente al caracter An y sea Ln la longitud de Cn. (Notar que Cn puede ser cualquier código)

Definimos al número de Kraft "K" como.

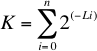
Se demuestra que para un código prefijo K debe ser menor o igual a uno, esta es la desigualdad de Kraft que no demostraremos aquí.

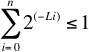 Desigualdad de Kraft

Esta desigualdad es fundamental pues si queremos un código decodificable sabemos que tenemos que satisfacer la desigualdad de Kraft.

Sabemos que la longitud Li de un código debe ser al menos -log2(Pi) para satisfacer la entropía, si además queremos que el código sea decodificable debemos pedirle que cumpla la desigualdad de Kraft, supongamos que Ei es la cantidad de bits que debemos agregar a la longitud determinada por la entropía para que el código sea decodificable.

Sea:

Li = - log₂(Pi) + Ei   (Ei es la longitud extra que debemos agragar)

2^(-Li) = 2^(--log₂Pi).2^-Ei    con    2log₂(Pi) = Pi

= Pi.2^(-Ei)

Planteando el número de Kraft y reemplazando Li por el valor calculado.

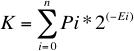
Sea Ei = E para todo i (caso más simple en el cual a todos la misma longitud)

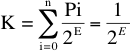
Por la desigualdad de Kraft.

2^(-E) <= 2⁰ (2⁰ = 1)

-E <= 0

E >= 0

Por lo tanto un código solo es decodificable si su longitud es mayor o igual a la determinada por la entropía.