Si la entropía es una medida del desorden, podemos escribir:
∆SS + ∆Sma = ∆Su (variación entrópica del universo)
Por lo tanto el universo tendrá una variación entrópica.
Aprovechando este concepto, enunciemos otra forma de la segunda ley:
La entropía del universo siempre aumenta
Esto es cierto para todos los procesos naturales y como tales espontáneos e irreversibles
∆Su> 0
y nunca puede ser menor que cero
Cálculos sencillos
Conocidos todos estos conceptos hagamos un cálculo sencillo para verificar que lo expresado cumple con nuestra intuición: Imaginemos dos cuerpos lo suficientemente grandes como para que al ponerse en contacto y transferir calor de uno a otro, ambos no sufran cambios en su temperatura.
Si el cuerpo A está calentado a 600 K y el B a 300 K es obvio que la transferencia de calor según nuestra experiencia debe realizarse de A hacia B. Propongamos una transferencia de 300 kJ y hagamos cálculos de las variaciones entrópicas correspondientes:
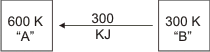
Gráfico número 22
SA = -300 kJ/600 K = - 0,5 kJ/K
SB= +300 kJ/300 K = + 1,0 kJ/K
∆Su = -0,5 kJ/K + 1,0 kJ/K = 0,5 kJ/K
Como se observa el S u > 0 y por lo tanto lo postulado coincide con nuestra experiencia.
Pero ahora vamos a plantear lo contrario o sea que un cuerpo más frío B entrega 300 kJ al A, cosa que sabemos nunca ocurre por si mismo es decir espontáneamente.
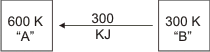
Gráfico número 23
SA =+300 kJ/600K =+0,5 kJ/K
SB =-300 kJ/300 K =-1,0 kJ/K
∆Su= + 0,5 kJ/K + (-1,0 kJ/K)= -0,5 kJ/K
Como se ve conduce a un resultado totalmente incorrecto e inconsistente con nuestra experiencia.
Entropías absolutas:
Hemos mencionado que la entropía es una medida del “desorden”. Ese desorden se manifiesta en las moléculas que forman una sustancia y en particular está relacionado con la energía térmica que U d. ya conoce. La distribución de las energías moleculares estudiada en loa gases se hace cada vez menos notable a medida que desciende la temperatura.
¿Qué queremos decir cuando hablamos de “cada vez menos notables”? :
Significa que todas las moléculas tenderán a tener un valor mínimo de energía que es igual en todas ellas. Recuerde que la distribución era de forma acampanada y ello indicaba que en un mol de gas podía haber moléculas con diferentes energías (particularmente de traslación) y que la energía cinética media es 3/2 R.T
¿Dónde se encontrará el límite?: En el cero absoluto donde todas las moléculas están “congeladas” y la entropía de todos los sólidos cristalinos perfectos (puros) es nula. Esto es una forma de expresar la tercera ley de la termodinámica sobre el cual no entraremos en mayores consideraciones.
Debemos aclarar que se dice sólidos cristalinos perfectos porque se debe cubrir la posibilidad de tener sólidos parcialmente desordenados en el cero absoluto.
Por lo tanto si tenemos sustancias (como por ej. pueden ser el Cu°, el Na°, etc.) que tengan entropías iguales a cero, es posible calcular así entropías absolutas (es decir valores reales). Esto como U d. sabe, no es posible para cálculos referidos por ejemplo a la entalpía, donde se estableció una convención arbitraria para efectuar los cálculos referidos a ella (entalpías estándar).
Como es evidente la temperatura y la presión son fundamentales determinarlas para saber qué valor de S será posible, y de ese modo se estableció un criterio similar al visto para la entalpía o sea establecer estados normales que en este caso como en el anterior será 25ºC y 1 atm de presión.
Se encuentran tabulados valores de S° (y no de ∆S°, como a lo mejor esperamos de acuerdo al comportamiento de la entalpía y energía interna de las sustancias).
Este hecho deriva, de la tercera ley de la termodinámica ya que se pueden calcular entropías absolutas.