Características de células para conversión solar

Células de silicio

Coeficiente de absorción en función de la longitud de onda

La brecha de energía, por la que se calcula la eficiencia teórica de conversión de materiales voltaicos, determina la absorción espectral característica del material en la región de absorción fundamental. El silicio tiene un corte de absorción en 1.2 u con fuerte aumento en el coeficiente de absorción hacia longitudes de onda mas larga. Esta característica se ve en la figura. La región fundamental es la región sensible de la célula de silicio.

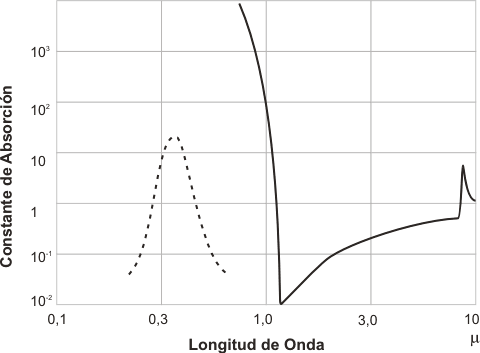
Respuesta espectral.

Por las características de absorción del silicio se ve que los fotones con energía de 1.02 e.v. o mas grande, pueden producir pres hueco-electrón. Sin embargo, la energía excedente de 1.02e.v. no se usa en el proceso de conversión de energía. La respuesta espectral de la célula fotovoltaica de silicio se da en la figura.

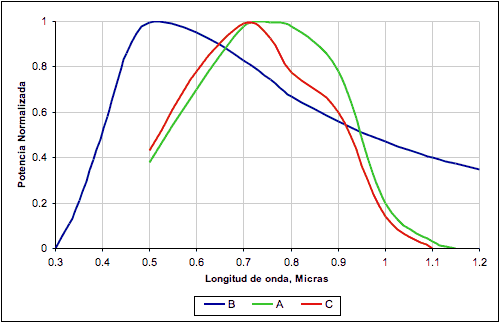
La curva A es el rendimiento de energía medido para intensidades iguales de radiación débil, en función de la longitud de onda. La sensibilidad máxima se ha tomado arbitrariamente como unidad. La curva C es el producto de las curvas A y B, reducidas de nuevo a la unidad para la sensibilidad máxima. Esta curva muestra cual es la porción útil de la radiación solar más útil para la célula.

Características del voltaje de corriente.

Tomando como base el circuito equivalente propuesto por Pfann y Van Roosbroeck, representado en la figura 12, y con las expresiones que describen las características del voltaje e intensidad del circuito, se hacen predicciones de la resistencia para la máxima transferencia de energía, el voltaje del circuito abierto y el voltaje e intensidad a la máxima energía.

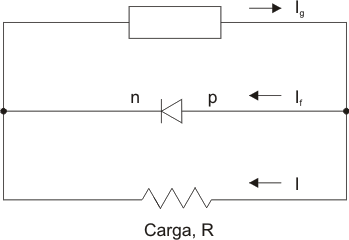
Las ecuaciones para este circuito equivalen a:

(1) I_g = I_f + I

(2) V = IR

(3)

En donde I_g es la intensidad de corriente generada, I_f la corriente que fluye en sentido opuesto, I la corriente en el circuito exterior y R₀ es la resistencia de la capa barrera con voltaje cero.

Para obtener una expresión de V en función de la intensidad en corto circuito, de la ecuación (1) se deduce:

(4) I_c.c. = I_f + I

La expresión de la energía máxima P = I V = I_c.c. - I_fV se deduce como:

Derivando e igualando la derivada a cero:

Con P máximo

(5)

Sustituyendo esta expresión en la ecuación (4) resulta:

(6)

Por la ecuación (6), se puede determinar la resistencia de carga para la energía máxima, en función de I_c.c. y R₀. De la ecuación (6) se deduce el voltaje y la intensidad máxima en función de R.

(7)

(8)

Con la ecuación (4) se determina el voltaje en el circuito abierto en función de la intensidad en corto circuito como sigue:

(9)

Se puede representar gráficamente una característica ideal de corriente de voltaje combinado las ecuaciones (1) y (3), que dan.

(10) I = I_g - I₀ (e^Dv/kf -1)

donde I₀ es la intensidad de saturación inversa y es igual a

En la figura se da la gráfica de esta ecuación obtenida con valores escogidos de los para metros. Mediante la elección adecuada de carga, es posible extraer casi 80% del producto I_c.c.V_c.a.