Este sistema esta basado en el álgebra lineal y ha sido importante en la historia de la criptografía. Fue Inventado por Lester S. Hill en 1929, y fue el primer sistema criptografico polialfabético que era práctico para trabajar con mas de tres símbolos simultaneamente.
Este sistema es polialfabético pues puede darse que un mismo caracter en un mensaje a enviar se encripte en dos caracteres distintos en el mensaje encriptado.
Suponiendo que trabajamos con un alfabeto de 26 caracteres.
Las letras se numeran en orden alfabético de forma tal que A=0, B=1, ... ,Z=25
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
Se elije un entero d que determina bloques de d elementos que son tratados como un vector de d dimensiones.
Se elije de forma aleatorea una matriz de d × d elementos los cuales seran la clave a utilizar.
Los elementos de la matriz de d × d serán enteros entre 0 y 25,
además la matriz M debe ser inversible en ![]() .
.
Para la encriptación, el texto es dividido en bloques de d elementos los cuales se multiplican por la matriz d × d
Todas las operaciones aritméticas se realizan en la forma modulo 26, es decir que 26=0, 27=1, 28=2 etc.
Dado un mensaje a encriptar debemos tomar bloques del mensaje de "d" caracteres y aplicar:
M×Pi=C, donde C es el código cifrado para el mensaje Pi
Ejemplo:
Si tomamos la matriz  como
matriz de claves.
como
matriz de claves.
Para encriptar el mensaje "CODIGO" debemos encriptar los seis caracteres de "CODIGO" en bloques de 3 caracteres cada uno, el primer bloque
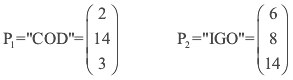
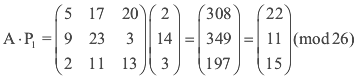
El primer bloque "COD" se codificara como "WLP"

El segundo bloque "IGO" se codificara como "GSE"
Luego 'CODIGO' encriptado equivale a 'WLPGSE'.
Observar que las dos "O" se codificaran de forma diferente.
Para desencriptar el método es idéntico al anterior pero usando la matriz inversa de la usada para encriptar.
Cálculo de la matriz inversa
Antes que nada debemos verificar que la matriz elegida sea invertible en modulo 26. Hay una forma relativamente sencilla de averiguar esto a través del cálculo del determinante. Si el determinante de la matriz es 0 o tiene factores comunes con el módulo (en el caso de 26 los factores son 2 y 13), entonces la matriz no puede utilizarse. Al ser 2 uno de los factores de 26 muchas matrices no podrán utilizarse (no servirán todas en las que su determinante sea 0, un múltiplo de 2 o un múltiplo de 13)
Para ver si es invertible calculo el determinante de A
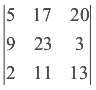
5 (23 · 13 – 3 ·11) – 17 (9 · 13 – 3 · 2) + 20 (9 · 11 – 23 · 2) =
1215 – 1734 + 1060 = 503
503 = 9 mod 26
La matriz A es invertible en modulo 26 ya que 26 y 9 son coprimos
Para hallar la inversa de la matriz modulo 26, utilizamos la formula ![]()
Donde CT es la matriz de cofactores de A transpuesta
Hay que tener en cuenta que ![]() debe
realizarse en modulo 26
debe
realizarse en modulo 26
por lo tanto para el ejemplo la inversa de 9 (mod 26) es 3 (mod 26) ya que
9 (mod 26) · 3 (mod 26) = 27 mod 26 = 1 (mod 26)
Por lo tanto 3 es la inversa multiplicativa de 9 en modulo 26
Para calcular C hay que calcular los cofactores de A
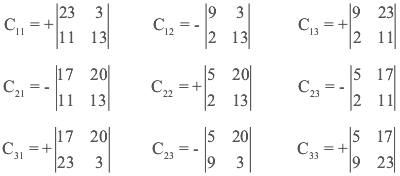
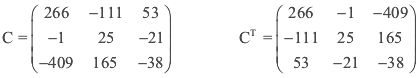
Ahora aplicamos la formula de la inversa
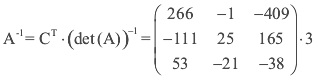

Esta última es la matriz que utilizamos para desencriptar
Criptoanálisis
El sistema de Hill plantea a los criptoanalistas problemas mucho mayores a los que planteaba 'CAESAR'. Para empezar el espacio de claves es mucho mayor, en este caso es de 4C25, es decir las permutaciones de 4 elementos tomados de entre 25 posibles. Y usando una matriz mas grande la cantidad de posibles claves se puede hacer tan grande como sea necesario para hacer que sea imposible un ataque por fuerza bruta.
Lo mejor que puede hacer un criptoanalista es tratar de conseguir un código para el cual se conozca una parte del mensaje. Y ver si con ambos datos es capaz de encontrar cual fue la matriz utilizada para encriptar el mensaje.