Consecuencias de la entalpía reticular

La ecuación de Born-Lande muestra que para una red cristalina tipo (con un valor conocido de A), la energía reticular aumenta al hacerlo las cargas de los iones Z⁺ y Z^- y al disminuir la distancia r entre los iones. Es decir, varía, de acuerdo con el parámetro electrostático c:

c = Z²/r

En este apartado se consideran tres consecuencias de la entalpía reticular y su correlación con el parámetro electrostático c.

Estabilidad térmica de los sólidos iónicos

El carbonato de magnesio se decompone cuando se calienta a 300 ºC, mientras que el de calcio sólo se descompone si se calienta a temperaturas superiores a los 800 ºC. Ello conduce a pensar que los cationes de gran tamaño son estabilizados por aniones grandes y vive versa. En particular, la temperatura de descomposición de compuestos inestables como los carbonatos aumenta con el radio del catión.

La influencia estabilizadora que proporciona un catión grande a un anión inestable puede explicarse en términos de la entalpía reticular. Considérese la descomposición térmica de un carbonato genérico:

MCO₃(s) MO(s) + CO₂(g)

La observación experimental de que la temperatura de descomposición aumenta al hacerlo el radio del catión puede expresarse en términos de la energía libre de Gibbs: ΔGr = ΔHr + TΔSr; la temperatura de descomposición se alcanzará cuando ΔGr = 0 y por lo tanto:

T = ΔHr/ΔSr

La entropía de descomposición es prácticamente constante para la mayoría de los carbonatos porque en todos los casos el factor dominante es la formación de dióxido de carbono gaseoso. Así pues, se espera que al aumentar la entalpía de reacción aumente también la temperatura de descomposición. La entalpía de reacción depende de la diferencia en entalpía reticular entre el producto de la descomposición, MO, y el carbonato de partida MCO₃. La entalpía de la reacción de descomposición es positiva (proceso endotérmico) pero será menos positiva si la entalpía reticular del óxido es mucho mayor que la del carbonato. Así, la temperatura de descomposición será baja para aquellos óxidos que tengan valores relativamente elevados de la energía reticular comparada con la del carbonato del cual procede. Los compuestos que cumplen este requisito son aquellos que están constituidos por pequeños cationes de elevada carga como el ion Mg²⁺.

La estabilidad de los estados de oxidación.

Un argumento similar se puede emplear para explicar el hecho de que los cationes de elementos en alto estado de oxidación se estabilizan por aniones pequeños. En particular, el ion fluoruro tiene una gran habilidad, en comparación con los otros halógenos, para estabilizar metales en altos estados de oxidación. Así, por ejemplo, los únicos haluros conocidos de Ag(II), Co(III) y Mn(IV) son los fluoruros. El átomo de oxígeno también es muy efectivo para estabilizar los estados de oxidación elevados porque, no sólo es pequeño, sino también puede aceptar hasta un máximo de 2 electrones. Para explicar estas observaciones consideremos la reacción:

MX + ½ X₂ MX₂

donde X es un halógeno. Se va a demostrar porqué esta reacción es fuertemente espontánea cuando X = F. Despreciando las contribuciones entrópicas, la reacción es más exotérmica cuando el halógeno es el flúor. A la entalpía de la reacción contribuye la conversión de ½ X₂ a X^-; a pesar de que el flúor tiene una afinidad electrónica menor que la del cloro, por ejemplo, este paso es más exotérmico para el F que para el Cl debido a la menor entalpía de enlace de la molécula F₂ comparada con la de Cl₂. Pero el factor de peso en la entalpía global de la reacción anterior es la energía reticular. Hay un cambio en el número de oxidación del catión en una unidad al pasar de MX a MX₂, de forma que la entalpía reticular aumenta en el mismo sentido. Si el radio del anión aumenta (por ejemplo al pasar de F^- a Cl^-), la diferencia entre las dos entalpías reticulares disminuye y la contribución exotérmica a la reacción global también disminuye. Tanto la entalpía reticular como la formación de X^- se hacen menos exotérmicos a medida que el halógeno cambia de F a I. Considerando que los factores entrópicos no cambian se espera un aumento en la estabilidad termodinámica de las especies MX respecto a MX₂ al descender en el grupo de los halógenos.

La solubilidad

Las entalpías reticulares juegan un papel importante en las solubilidades de los compuestos iónicos aunque este factor es más difícil de analizar que los anteriores. En general, los compuestos que poseen iones de muy diferentes radios son solubles en agua. Por el contrario, las sales más insolubles son aquellas que poseen iones de radios similares. La regla general que puede inferirse es que la diferencia en tamaño favorece la solubilidad en agua. Experimentalmente se encuentra que un compuesto iónico MX tiende a ser más soluble si el radio del catión es menor que el del anión en 0.8 Å.

Para intentar racionalizar estas observaciones hay que considerar que la solubilidad de un compuesto iónico depende de la energía libre de Gibbs asociada al siguiente proceso:

MX(s) M⁺(ac) + X^-(ac)

En este proceso, las interacciones responsables de la entalpía reticular son sustituidas por las entalpías de hidratación o solvatación de los iones. Sin embargo, el balance exacto entre los efectos entálpicos y entrópicos es delicado y de difícil acceso, particularmente porque los cambios entrópicos dependen del grado de orden de las moléculas del disolvente que se modifica por la presencia del soluto disuelto. Los datos que se muestran en la Figura 16 sugieren que los valores entálpicos son más importantes en algunos casos existiendo una correlación entre la entalpía de disolución de una sal y la diferencia en las entalpías de hidratación de los dos iones. Si el catión posee una energía de hidratación mucho mayor que la del anión (lo que refleja diferencia en los tamaños de ambos iones) o viceversa, la disolución de la sal es un proceso exotérmico. La variación en entalpía puede visualizarse aplicando el modelo iónico. La entalpía reticular es inversamente proporcional a la distancia entre los dos iones:

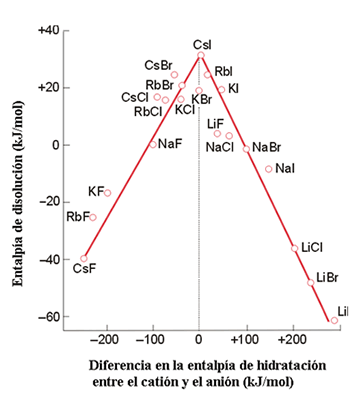
Figura 16. Correlación entre la entalpía de disolución de un compuesto iónico y las entalpías de hidratación de los iones

ΔH_U a 1/r⁺r^-

mientras que la entalpía de hidratación es proporcional a la suma de las contribuciones iónicas individuales:

ΔH_hidr a (1/r⁺) + (1/r^-)

Si uno de los iones es pequeño, el término correspondiente a la entalpía de hidratación de dicho ion es grande. Sin embargo este factor no hace que el denominador de la expresión de la entalpía reticular se haga pequeño por sí sólo. Es decir, un ion pequeño origina una elevada entalpía de hidratación pero no necesariamente una gran entalpía reticular, de forma que los iones asimétricos son los que proporcionan un proceso de disolución exotérmico. Sin embargo, si ambos iones son pequeños entonces tanto las entalpías de hidratación como la energía reticular serán grandes y la disolución puede no ser un proceso exotérmico.