Ya se ha comentado en un capítulo anterior la definición del radio iónico como el resultado de una partición de la distancia internuclear entre dos iones consecutivos y de distinto signo en una red cristalina. En aquel momento se explicó la utilidad del uso del radio del anión óxido O= (1.40Å) como base para la escala de radios iónicos. Pero además en el apartado de radios metálicos ha aparecido una nueva dificultad: el incremento del radio iónico conforme aumenta el número de coordinación. La Figura 12 muestra la variación del radio iónico con este parámetro, y obviamente ello supone la necesidad de tener esto en cuenta cuando se efectúen comparaciones entre distintos compuestos.
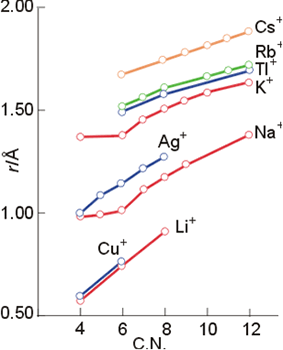
Figura 12. Variación del radio iónico con el número de coordinación
Un parámetro muy empleado para predecir el número de coordinación es la denominada relación de radios
ρ = r< / r>
donde r< significa el radio del menor ion y r> el del mayor ión. El valor de ρ permite aventurar el número de coordinación. La Tabla 4 muestra la relación de radios y las correspondientes coordinaciones que se derivan de ellas. Estos cálculos están hechos en base a consideraciones geométricas, y por ello presentan limitaciones. De hecho, son bastante más fiables cuanto mayor sea el número de coordinación.
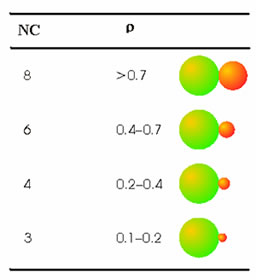
Tabla 4. La relación de radios
La energía del enlace iónico
La entalpía o energía reticular, ΔHU, de un compuesto iónico se define como el cambio entálpico que se produce cuando 1 mol de iones positivos y un mol de iones negativos, ambos en estado gaseoso, se aproximan desde distancia infinita hasta las posiciones de equilibrio que ocupan en el cristal:
M+(g)
+ X-(g) ![]() MX(s)
MX(s)
La entalpía reticular es siempre negativa, es decir, la formación del sólido iónico es un proceso exotérmico. Una forma de calcular la entalpía reticular es mediante el ciclo de Born-Haber. Este ciclo es una consecuencia de la ley de Hess que enuncia que la entalpía de una reacción es la misma con independencia de que la reacción transcurra en uno o en múltiples pasos. Para la formación de un cristal iónico a partir de los elementos que lo constituyen se puede plantear el siguiente ciclo de Born-Haber:
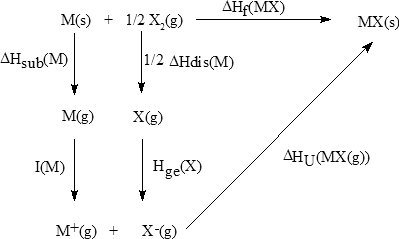
donde,ΔHsub = entalpía de sublimación del metal
ΔHdis = entalpía de disociación del no metal
I = energía de ionización del metal
Hge = afinidad electrónica del no metal
ΔHU = entalpía reticular
ΔHf = entalpía de formación de un compuesto a partir de sus elementos
Aplicando la ley de Hess resulta:
ΔHf = ΔHsub + 1/2 ΔHdis + I + Ae+ ΔHU
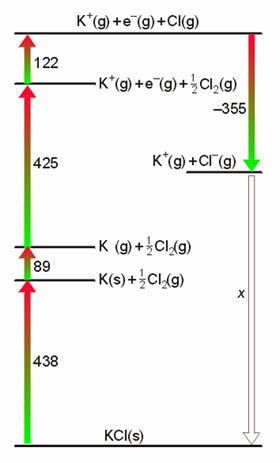
Figura 13. Ciclo de Born-Haber para el KCl.
La Figura 13 presenta un esque del ciclo de Born-Haber aplicado al cloruro potásico, construido a partir de los siguientes datos:
Paso |
ΔH(kJ/mol) |
|---|---|
Sublimación del K |
+89 |
Ionización del K(g) |
+425 |
Disociación del Cl2(g) |
+244 |
Ganancia e del Cl |
-355 |
Formación del KCl(s) |
-438 |
De aquí se deduce que el valor de la energía reticular es de ΔHU(KCl(s)) = -719 kJ/mol.
Una vez calculada la energía reticular por este procedimiento, en lo que puede considerarse un valor experimental, ya que está calculado a partir de otros datos experimentales, es preciso obtener un valor teórico sobre la base de un modelo iónico. Este modelo iónico está basado, única y exclusivamente, en interacciones de tipo coulombianas. Si ambos valores son similares significa que el compuesto es puramente iónico, pero si existen fuertes discrepancias entre el valor experimental y el teórico entonces significa que hay una importante contribución de tipo covalente al enlace en el sólido.