Por Alejandro R. Álvarez Silva
Verdaderamente, habría que apellidar este bosón, no como lo hizo el premio nobel Leon Lederman, “la partícula de Dios”, sino más bien, “la partícula de oro”, si nos atenemos al descomunal esfuerzo “en presupuesto” realizado por gobiernos e instituciones científicas de medio mundo, al construir el mayor acelerador de partículas hasta el presente, el LHC (Large Hadron Collider). Es por ello por lo que irónicamente he rebautizado al bosón de Higgs como “partícula de oro” y no “divina”, aunque a decir verdad ni el oro justificaría el fantástico despliegue de medios aportados en este proyecto… ¡por eso la denominación de Lederman encaja mejor con su presupuesto, más propio de la “divinidad”!
Bromas aparte, hay que decir que el bosón de Higgs no es más que una “etiqueta” o bandera sobre la que quiere acogerse la propia justificación de los fantásticos gastos en medios y personal realizados por el CERN para construir el engendro tecnológico que supone el LHC. Ahora bien, el avance que se espera obtener en investigación básica y aplicada (tan sólo hasta ahora), que incide directamente en las mismas fronteras de la Ciencia, sí justificaría este desembolso.
Pero ciñéndonos al tema, ¿cuál es en realidad la importancia de la búsqueda del bosón de Higgs?... El bosón de Higgs es una partícula que aparece en el modelo estándar de la física de partículas por la aplicación del llamado “mecanismo de Higgs”. Así que, en realidad, la búsqueda del bosón de Higgs es la puesta en práctica de los experimentos necesarios para poner a prueba un elemento indispensable hoy en la teoría estándar denominada SU(3)⊗SU(2)⊗U(1): el “mecanismo de Higgs”. Los científicos Steven Weinberg y Abduz Salam fueron los primeros en aplicar este mecanismo a la ruptura espontánea de simetría electrodébil.
Pero no adelantemos acontecimientos.
La básica ecuación de Schrödinger de la mecánica cuántica, en su forma común:
[- ħ2/2m ∇2+ V(r) ] ψ (r,t)= i ħ ∂ψ/∂t (r,t) (1)
(donde ψ es la función de onda de una partícula, m su masa y V su energía potencial)
tiene dos inconvenientes en su aplicación a la QFT (Quantum Field Theory) o teoría cuántica de campos (la teoría cuántica del campo electromagnético es la conocida electrodinámica cuántica, de extraordinaria precisión, desarrollada en los años 20 y 50 por Dirac, Fock, Pauli, Tomonaga, Schwinger, Feynman y Dyson):
- No es relativista, pues descuida la posibilidad de “crear” o “destruir” partículas dinámicamente, algo que para la famosa relación masa-energía de Einstein (E=mc2) es crucial –por ejemplo, un electrón y un positrón pueden aniquilarse para crear fotones.
- Se complica grandemente, hasta llegar a ser irresoluble, cuando se aplica a una gran cantidad de partículas. Y es que las partículas mecánico-cuánticas de la misma especie son indistinguibles, puesto que la función de onda del conjunto entero debe ser simétrica (bosones –fotón, etc.) o antisimétrica (fermiones –electrón, etc.) cuando las coordenadas de sus partículas se intercambian.
Por ejemplo, la función de onda general de un conjunto de N bosones se escribe:
Φ(r1, r2,……,rN)= 1/ √N! Σp Φp(1) (r1)……….Φp(N)(rN) (2)
ri son las coordenadas de la partícula –i-ésima.
Φi la función de onda de cada partícula.
Que es una suma (N factorial) N! de términos distintos, que con el aumento de N se hace inmanejable.
Respecto a (1), para hacerla invariante respecto a la transformación relativista de Lorentz, se toma:
Ψ(t, r)= exp (ikr-iw(k)t) donde (relación de Broglie) p= ħk (3)
Con esto, y determinando la frecuencia w(k) por la condición de que la velocidad de grupo coincida con la velocidad observada de la partícula, se llega a la ecuación cuántica relativista más sencilla, KGB o ecuación Klein-Gordon-Fock:
(∂2+m2c2/ħ2) ψ (t,r)=0 (4)
El procedimiento por el que los campos cuánticos se construyen a partir de partículas individuales fue introducido por Dirac y se conoce como segunda cuantización.
El campo cuántico aquí referido no es el de la dualidad onda-partícula (entidades que poseen propiedad de onda y partícula puntual a la vez, y que no se localizan en un punto dado, sino que simplemente tienen cierta probabilidad de ser encontradas en cada partícula en el espacio), sino que este “campo” es una entidad que existe en cada punto en el espacio, y que regula la creación y aniquilación de las partículas. Y como todo sistema cuántico, un campo cuántico posee un hamiltoniano H (concepto ligado a la energía total), que obedece a “la ecuación de Schrödinger usual” –otra forma de (1)–:
H | ψ (t) › = i ħ ∂/∂t | ψ (t) › (5)
Pero la teoría del campo cuántica es formulada muy a menudo en términos de lo que se llama un “lagrangiano”, técnicamente debido a lo que se denomina “covariancia explícita”. Pero las formulaciones tanto lagrangianas como hamiltonianas se toman como equivalentes.
Así que el formalismo matemático denominado segunda cuantización se emplea para estudiar tanto los sistemas de muchas partículas idénticas con interacciones arbitrarias, como la teoría cuántica de campos. Sabemos que el teorema espín-estadística establece relaciones de conmutación que clasifican a las partículas en bosones y fermiones.
Si | ψ › es la función de onda para una partícula, con la segunda cuantización pasaría a ser un operador no-hermítico (*) ψ que actúa sobre un estado del espacio-tiempo, como por ejemplo el que representa el vacío | 0 ›. La actuación del operador sobre dicho estado representa el estado del espacio-tiempo una vez se ha creado una partícula con esta función de onda | ψ › habiendo dejado de ser el espacio vacío:
ψ† | 0 › = | ψ ›
Así se interpreta que ψ† “crea” una partícula en el mencionado estado. Su operador adjunto ψ “destruiría” dicha partícula (o equivalentemente crearía una antipartícula). Si | 1 › denota un estado con una partícula del tipo correcto entonces:
Ψ | 1 › = | 0 ›
*Un operador hermítico (definido sobre un espacio de Hilbert –generalización del concepto de espacio euclídeo-) es un operador lineal que, sobre cierto dominio, coincide con su propio operador adjunto y tiene la propiedad de que sus autovalores son siempre números reales. (Si el espacio de Hilbert es de dimensión finita todo operador hermítico es además autoadjunto, y viene dado por una matriz semítica y diagonizable).
Una matriz es hermética o autoadjunta cuando es igual a su propia adjunta y antihermítica cuando es igual a su traspuesta conjugada multiplicada por -1. Y en espacios vectoriales reales, las matrices hermíticas coinciden con las matrices simétricas y las antihermíticas con las antisimétricas.
En la formulación de la mecánica cuántica de Dirac-von Newmann, los posibles valores de los observables físicos o magnitudes físicas, son los autovalores de ciertos operadores que representan la magnitud física, así que para que un operador pueda interpretarse como una magnitud físicamente medible requiere que sus autovalores sean números reales, condición garantizada si los observables se representan por operadores herméticos.
Y la consecuencia más importante de que un operador hermítico sea además autoadjunto es que entonces se le puede aplicar el teorema de descomposición espectral.
Todos los operadores importantes de la mecánica cuántica como la posición, el momento, el momento angular, la energía o el espín se representan como operadores autoadjuntos en un dominio denso del espacio de Hilbert L2 (ℝ3).
Como dijimos, el operador hamiltoniano, definido por:
Ĥ ψ = - ħ2/2m Δ ψ + V ψ (6)
es un observable correspondiente a la energía total de una partícula de masa m en un campo de potencial V.
Las ecuaciones de onda relativistas para una partícula son:
- Ecuación de Klein-Gordon para partículas sin espín, que en el límite no relativista, como hemos visto, se reduce a la ecuación de Schrödinger.
- Ecuación de Dirac para partículas de espín ½ (electrón, etc.), que en el límite no relativista se reduce a la ecuación de Schrödinger-Pauli. (Asociada a la invariancia respecto a la paridad-helicidad no fija):
i ħ ψ· = i ħ c α ∇ ψ + mc2 β ψ
siendo ψ un “bispinor” (en realidad dos fórmulas con dos spinores distintos –partículas y antipartículas-), con las matrices de Dirac 4х4:
α = ( 0σ σ0 ) , β = (10 01) - Ecuación de Rarita- Schwinger para partículas de espín 3/2.
Los operadores del campo pueden ser construidos aplicando la transformación de Fourier a los operadores de creación y aniquilación. Por ejemplo, el operador de aniquilación del campo bosónico es:
Φ (r) ≡ Σi eiki.r ai
El hamiltoniano escrito en términos de los operadores de creación y aniquilación, o los operadores de campo queda:
H = Σk Ek ak† ak
que describe un campo de bosones (que no interactúan) libres, donde Ek es la energía cinética del k-ésimo modo del momento
Las teorías extensamente aceptadas del modelo estándar son teorías de campo de gauge, que es un tipo de teoría cuántica de campos basada en el hecho de que la interacción entre fermiones puede ser vista como el resultado de introducir transformaciones “locales” pertenecientes al grupo de simetría interna en el que se base la teoría gauge, simetría interna abstracta conocida como invariancia de gauge. En el lenguaje matemático se inscriben en la geometría diferencial, e involucran transformaciones gauge o transformación de algún grado de libertad interno, que no modifica ninguna propiedad observable física.
Como ejemplo, el campo electromagnético es un campo de gauge que describe el modo de interactuar de fermiones dotados de carga eléctrica.
La invariancia gauge significa que el lagrangiano que describe el campo es invariante bajo la acción de un grupo de Lie (una variedad diferenciable real o compleja que es también un grupo tal que las operaciones de grupo –multiplicación e inversión- son funciones analíticas. Los grupos de Lie son importantes para estudiar simetrías de ecuaciones diferenciales. El espacio euclídeo Rn es un grupo de Lie real con la adición ordinaria de vectores como operación de grupo. Otro ejemplo es el grupo SO(3) de todas las rotaciones en el espacio de 3 dimensiones –grupos de matrices inversibles con la multiplicación de matrices-) que actúa sobre las componentes de los campos.
Para formular una teoría de campo gauge es necesario que la dinámica de los campos fermiónicos de la teoría venga descrita por un lagrangiano que tenga alguna simetría interna “local” dada por un grupo de Lie, llamado grupo de transformaciones de gauge. Al “rotar” algo en cierta región (se usa el término “rotar” porque los grupos de gauge más frecuentes son SU(2) y SU(3) que son generalizaciones del grupo de rotaciones ordinarias), no determina cómo los objetos rotan en otras regiones (no se modifica ninguna propiedad observable física).
La idea para explicar la existencia de las otras interacciones, además de la electromagnética, es una generalización de la invariancia gauge a las partículas que tienen varios estados internos a = 1,2,…., N. Su función de onda será la que satisfaga la ecuación de Schrödinger:
i ħ c ∂o (t,r) = -(ħ2/2m) ∇2 ψa (t,r) (7)
con la notación relativista ∂o = (1/c) ∂/∂t.
Se demuestra que la teoría de una partícula con N estados internos con la ecuación de Schrödinger anterior es invariante respecto a las transformaciones de la función de onda ψ = {ψa} por matrices U unitarias N×N constantes cualesquiera. Matemáticamente tales transformaciones forman el grupo U(N) global, que incluyen como caso particular las transformaciones consistentes en multiplicar cada componente por el mismo factor de fase exp(i α), que sirven para introducir la interacción electromagnética; se denominan abelianas y son muy sencillas. Cuando aparecen estados internos, o sea, cuando N>1, estamos ante transformaciones no abelianas SU(N), de las que hay que excluir las anteriores abelianas, es decir, las diagonales con todos los elementos iguales a exp (i α).
Para hacer la ecuación de Schrödinger invariante, suponemos que la partícula interacciona con cierto campo externo análogo al campo electromagnético, compuesto por el escalar βo (t,r) y el vectorial β (t,r) unidos en un 4-vector relativista βμ (t,r) , μ = 0,1,2,3 que experimenta la transformación gauge precisamente de tal forma que compensa el cambio producido en la ecuación de Schrödinger, que se transforma en:
i ħ c (∂o+ig βo (t,r)) ψ = -(ħ2/2m) (∇+ig β (t,r))2 ψ (8)
con la constante de acoplamiento g análoga a la carga eléctrica.
El factor i se ha separado para que el campo de β se presente como una matriz hermética: la componente βo se añade al hamiltoniano y la β al momento, que son operadores herméticos.
Haciendo la transformación del campo β:
β´ = U β U-1 – (1/g) U (∂U-1) (9)
y tomando ψ´ = U ψ
se tiene:
i ħ c (∂o+ig βo´) ψ´ = - (ħ2/2m) (∇+ig β´)2 ψ´ (10)
O sea, (8) y (10) se identifican, es decir, se ha conseguido la invariancia de la ecuación de Schrödinger bajo las transformaciones SU(N) locales a costa de introducir un campo matricial β con la transformación gauge apropiadamente ajustada en relación con la transformación de la función de onda.
La ecuación de movimiento para el campo gauge β debe poseer la invariancia relativista y la invariancia gauge bajo la transformación (9), además debe ser compatible con la ecuación de Schrödinger para la función de onda de la partícula. El método adecuado es el de Lagrange. En vez de escribir las ecuaciones para cada componente por separado y ver su compatibilidad, se construye una funcional que depende de todas las variables del sistema, la acción, y se busca un extremo (el mínimo).
El mínimo se realiza cuando las variables satisfacen ciertas ecuaciones que son automáticamente compatibles y que son precisamente las ecuaciones del movimiento buscadas. Más aún, si queremos que las ecuaciones posean alguna simetría, basta exigir que la tenga la acción, y así tendremos la invariancia deseada.
La ecuación definitiva para el campo gauge β resulta:
∂2 βμ - ∂μ (∂β) = jμ+Jμ (11)
donde en la parte derecha las corrientes (j) provienen tanto de la partícula (jμ) con los estados internos, como del propio campo gauge (Jμ). Por consiguiente, a diferencia del campo electromagnético, el campo gauge no abeliano interacciona consigo mismo.
Con la interacción (g ≠ 0), entonces, el campo gauge no abeliano se distingue del electromagnético en dos aspectos claves. Uno, en que interacciona consigo mismo, por poseer una carga no trivial respecto a la interacción. Y dos, por su modo de interacción con las distintas partículas.
Se postula que la interacción débil (hay cuatro interacciones: gravitatoria, electromagnética, débil y fuerte) posee la invariancia SU(2) respecto a las transformaciones unitarias con determinante unidad del doblete:
ν L
ΨL = ( e L ) neutrinos y electrones de izquierda.
Podemos considerar sus dos estados νL y eL como correspondientes a los dos valores posibles, +1/2 y -1/2, de una magnitud análoga a la proyección del espín ordinario y del isospin para el protón y el neutrón, que se refiere a los estados internos del doblete de izquierda. Esa magnitud se llama isospin débil Iw, o sencillamente I, porque aquí no vamos a hablar del isospin ordinario. Esta simetría SU(2) se llama por eso la simetría del isospin débil SU1(2). Se supone que dicha simetría es local. Por eso se introduce el campo gauge W correspondiente, una matriz 2×2 hermítica con la traza igual a cero, que interacciona con el doblete ψL y consigo mismo.
El electrón de derecha no cambia bajo las transformaciones del isospin débil SU(2), tiene I = 0. Por consiguiente, no toma parte alguna en la interacción con W.
Esta es la demostración de que no podemos limitarnos tan solo a las transformaciones SU(2), sino que hay que introducir además transformaciones de fase análogas a las electromagnéticas, abelianas, que forman un grupo U(1) llamado grupo de hipergarga Y. La simetría total de la teoría primaria es por tanto SU1(2)⊗Uy(1).
El electrón de derecha eR tiene la misma carga que el izquierdo y sus transformaciones deben ser idénticas. Pero el de derecha se transforma sólo por la hipergarga
La simetría U(1) de hipergarga también se supone local, y así se introduce el campo gauge correspondiente C, análogo al electromagnético, que interacciona con la hipercarga de las partículas, o sea, tanto con ψL como con eR.
Así queda construida la teoría inicial con la simetría exacta. La función de Lagrange es la suma de cuatro términos:
£ = £L+£R+£w+£C (12)
La parte £L describe los leptones de izquierda y sus interacciones con W y C:
£L = ψL* (iα, ∂+igLW+igY C/ 2½) ψL (13)
α = {1, α} son matrices de Dirac. Los campos W y C 4-vectores relativistas, igual que ∂.
£R describe el electrón de derecha y su interacción con el campo C:
£R = eR* (iα, ∂+igY C/ 2½) eR (14)
Las partes £w y £C describen los propios campos gauge:
£w = -(1/4) Tr F2 , £C = -(1/4) G2 (15)
Donde:
Fμν = ∂μWν - ∂νWμ +igL (Wμ , Wν)
Gμν = ∂μCν - ∂νCμ μ , ν = 0,1,2,3 (16)
Por tanto el campo W interacciona consigo mismo y el C no interacciona.
Formando la acción completa:
a = ∫ d4x £ (17)
Y buscando su extremo se encuentran las ecuaciones del movimiento para todas las funciones ψL, eR, W y C. Por ejemplo para ψL resulta la ecuación:
(iα, ∂+ig+W+igY C/2½) ψL = 0 (18)
que es la ecuación de Dirac con la masa nula y con la interacción con los campos W y C. Asimismo para el eR:
(iα, ∂+igY C/2½) eR = 0 (19)
que es también la ecuación de Dirac con la masa nula y con la interacción con el campo C. Vemos que la simetría intacta corresponde a las masas de leptones iguales a cero. No es un hecho fortuito. La masa en la ecuación de Dirac mezcla las dos partículas de izquierda y derecha.
Volviendo a los campos gauge W y C, sabemos que satisfacen las ecuaciones del movimiento (11), que son las ecuaciones de Maxwell con las fuentes proporcionadas por los leptones y por el propio campo W. Después de la cuantización los campos W y C describen cuatro bosones gauge en total, con la masa nula todos ellos.
Los elementos de la matriz W son: W- que describe partículas cargadas negativamente como el electrón; W+ que describe sus antipartículas cargadas positivamente, como el positrón; y las componentes diagonales que son reales y describen partículas neutras W0/2½, con la traza nula. Así:
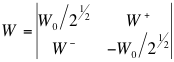
El campo C es real y describe partículas C0 neutras, como los fotones.
La interacción entre el doblete ψL y los campos W y C se describen por el término en la función de Lagrange:
ψL* (igLW+igv C/2½, iα) ψL (21)
que se escribe a través de los campos con la carga definida como:
igL ((CW+, νi* αeL)+(W-, eL*i αν))+(i/2½) ((gLW0, (νi* αν –eL* iα eL))+(gYC, (ν* iαν+eL* iα eL)) (22)
después de la cuantización, en términos de creación y aniquilación de partículas. El primer término corresponde a los procesos con desaparición de la carga del leptón:
e ⇒ W- + γ , e + W+ ⇒ γ (23)
y los análogos con las antipartículas. El segundo describe los procesos donde, por el contrario, el neutrino pasa al leptón cargado:
γ ⇒ e + W+ , γ + W- ⇒ e (24)
y los dos análogos con las antipartículas. Los últimos términos de (22) son similares a los que tenemos en la interacción electromagnética: describen la emisión o absorción de W0 o C0 por neutrinos o electrones de izquierda más los procesos de aniquilación y creación de pares νν- o eL eL+.
El electrón de derecha toma parte sólo en la interacción en C.
Las reacciones (23) y (24) corresponden plenamente a la interacción débil observada. Pero por ahora las masas de todas las partículas son nulas y no se ha distinguido ninguna interacción que pueda jugar el papel de la electromagnética, con la conservación de la paridad.