Calorímetro

Medida de la capacidad calorífica y calores específicos

La capacidad calorífica de un sistema puede ser negativa, nula, positiva o infinita, según el tipo de proceso que experimente el sistema durante el intercambio de calor, ya que como vimos antes, el calor depende del camino o proceso para obtener el incremento de temperatura. Si el proceso se realiza a presión constante, la capacidad calorífica se denomina a presión constante y se designa por el símbolo C_p. Será entonces:

Análogamente, en un proceso a volumen constante se puede definir la capacidad calorífica a volumen constante que se expresa por la relación:

Donde Q_p y Q_v son las cantidades elementales de calor intercambiadas a presión y volumen constante respectivamente.

C_p depende de P y T y C_v depende de V y T. En general C_p y C_v son distintas y toman valores particulares para cada sistema. Aunque las capacidades caloríficas son funciones de dos variables, dentro de un intervalo pequeño de variación, pueden considerarse constantes.

En el caso de un sólido o de un líquido los valores de C_p y C_v son muy parecidos, pero en un gas son muy distintos. En los métodos de medida de la capacidad calorífica cuyos fenómenos ocurran a presión constante, las capacidades y calores específicos medidos, corresponderán entonces a presión constante.

Entre los métodos utilizados para medir capacidades caloríficas o calores específicos podemos distinguir fundamentalmente el método eléctrico y el método de las mezclas.

El primero se utiliza modernamente casi con exclusividad ya que las medidas pueden hacerse con un alto grado de precisión. El método de las mezclas solo da una medida aproximada del valor medio de C_p en un intervalo de temperatura próximo a la temperatura ambiente.

El recipiente utilizado para efectuar las medidas de calor se denomina calorímetro, que en su forma más sencilla es una vasija de paredes aisladas que aloja en su interior el termómetro y agitador. Además contiene un líquido calorimétrico que generalmente es el agua.

Equivalente en agua del calorímetro

Para efectuar medias calorimétricas es necesario conocer la capacidad calorífica de los elementos que forman el calorímetro. Es evidente que para un mismo aparato la suma de dichas capacidades caloríficas será una constante, y se la ha denominado “equivalente en agua del calorímetro”. Se define como equivalente en agua del calorímetro al peso de agua que necesita la
misma cantidad de calor que el termómetro, agitador, paredes del calorímetro, etc, para elevar su temperatura el mismo número de grados. El equivalente en agua es así la capacidad calorífica de una masa de agua, de igual valor a la suma de las capacidades caloríficas de los elementos del calorímetro, se expresa en cal. grado^-1. Se determina experimentalmente.

Calorímetro de las mezclas

Este aparato tiene la característica ya descripta y ha sido denominado impropiamente calorímetro de agua. Las determinaciones se efectúan a intervalos de temperaturas próximas a la temperatura del medioambiente; y se supone que el calor específico del agua es constante e igual a la unidad.

El método consiste en introducir en el calorímetro una cantidad conocida de agua, a una temperatura determinada, y luego colocar dentro de ella cierta masa de la sustancia cuyo calor específico se desea conocer y a una temperatura superior conocida. Se mide la elevación de temperatura del agua, hasta que alcance el equilibrio térmico con la sustancia problema.
Si llamamos M₁ a la masa del agua, t₁ a su temperatura inicial que es la misma del calorímetro;

M_t, M_a M_p las masas del termómetro, agitador y paredes del calorímetro cuyos calores específico son respectivamente c_t , c_a y c_p ; m₂ la masa de la sustancia cuyo calor específico c₂ se desea conocer y que se introduce a temperatura t₂; y por último t a la temperatura de equilibrio, siendo t₂ > t > t₁; de acuerdo a la definición de calor específico, medio, el calor cedido por la sustancia problema será:

Q₂ = M₂.c₂.(t₂ − t)

Y el calor absorbido por el agua, las paredes del calorímetro, el termómetro y agitador: siendo el calor específico del agua igual a 1).

Q₁ = (M₁ + M_t .c_t + M_a .c_a + M_p .c_p) . (t - t₁)

Como los cuerpos forman parte de un sistema aislado y solo intercambian calor, deberá ser: Q₁ = Q₂; además, de acuerdo a la definición de equivalente en agua

E = M_t .c_t + M_a .c_a + M_p .c_p

En consecuencia

M₂ .c₂ (t₂ − t) = (M₁ + E) (t − t₁)

De donde

Esta expresión permite calcular el calor específico medio de la sustancia entre las temperaturas t₂ y t.

El equivalente en agua del calorímetro E se puede determinar agregando una masa conocida de agua M₂, a temperatura t₂ sobre otra de agua M₁ a temperatura t1 inferior a t₂. Siendo t la temperatura de equilibrio, se deberá cumplir de acuerdo con lo dicho anteriormente que:

M₂ (t₂ − t) = (M₁ + E) (t − t₁)

De donde:

También se puede determinar el valor de E colocando en la masa M₁ de agua, a temperatura t₁, un conductor eléctrico de resistencia conocida R y pasando una intensidad de corriente definida i durante un tiempo determinado T hasta temperatura t.

La energía eléctrica consumida se transmite totalmente al agua en forma de calor, de acuerdo con la expresión:

0,24.R.i² .τ = Q (cal) = (M₁ + E) (t − t₁)

De donde:

Métodos modernos de medida de los calores específicos

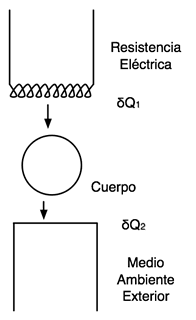
Los métodos modernos de deidad de calores específicos se basan en una doble transferencia simultánea de energía por parte del cuerpo cuyo calor específico va a determinarse. Por una parte recibe calor de una resistencia eléctrica y por el otro cede calor al medio más frío que lo rodea.

En un intervalo de tiempo infinitesimal, dT, el calor absorbido por el sistema será:

δQ = δQ₁ − δQ₂ = c.dt

Siendo R el valor de la resistencia, i la intensidad de corriente, δQ₁ = 0,24.R.i² .dτ

luego

Medida de c_v

Los métodos de medida que hemos descriptos se utilizan para la determinación de los calores específicos a presión constante c_p. Como para un sólido la medida precisa de c_v es casi imposible, se mide primeramente c_p y luego se utilizan fórmulas teóricas que relacionan c_p y c_v. Lo mismo se hace en el caso de los líquidos y los gases.

En estos últimos c_p y c_v están relacionados por las ecuaciones del exponente adiabático y de Mayer.