Flujos de Entrada
La diferencia primordial entre flujo interno y externo se encuentra en que, en flujo interno, en la región de entrada existe una capa limite y una corriente libre uniforme, que se acelera de acuerdo a la tasa de crecimiento de la capa limite; existe además una segunda y más importante diferencia que es cuando el flujo se hace completamente desarrollado. En tal caso, la velocidad varia sobre todo el conducto y no hay corriente libre o capa limite bien definida y delimitada.
Se considera la región de entrada para flujo laminar, como se indica en la figura siguiente:
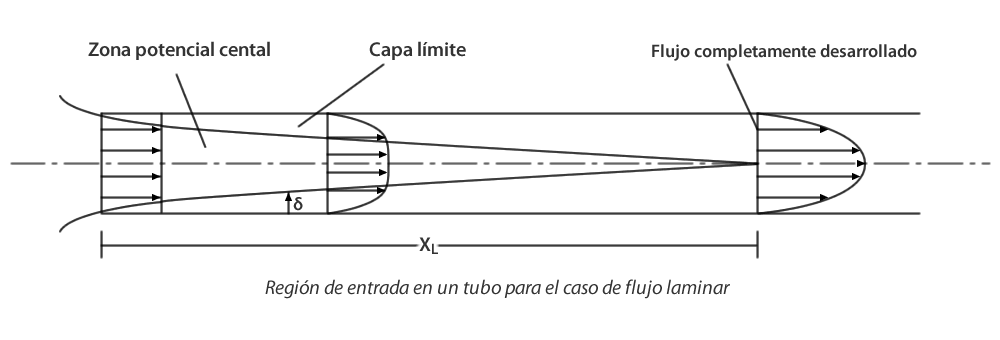
Región de entrada en un tubo para el caso de flujo laminar
La velocidad es uniforme a la entrada y la capa limite crece con la distancia desde la entrada hasta que el flujo está completamente desarrollado. De la ecuación de continuidad, se observa que la parte central del flujo debe acelerarse; a través de la ecuación de Bernoulli a lo largo de una linea de corriente en esta región de corriente libre se observa que la presión debe decrecer. La longitud XL para que el flujo laminar quede completamente desarrollado es XL = 0,03 NRe D.
La figura siguiente muestra e! flujo en la región de entrada para el caso en que NRe es suficientemente grande para que el flujo se haga turbulento.
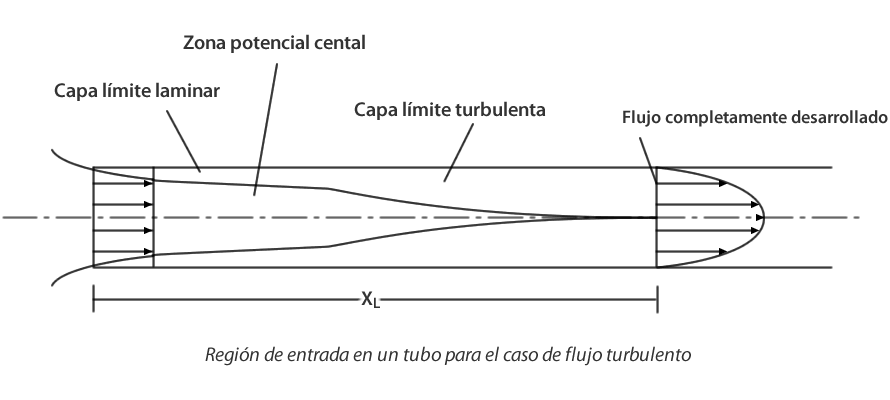
Región de entrada en un tubo para el caso de flujo turbulento
Existen varias formas de establecer el criterio para que el flujo sea completamente desarrollado. Así, se puede definir el flujo completamente desarrollado según la caída de presión, distribución de velocidad media o cantidades de turbulencia. Cada criterio lleva a longitudes XL reales diferentes. El gradiente de presión requiere generalmente una longitud de 3 a 4 veces el diámetro para desarrollarse; la velocidad media requiere una longitud entre 30 y 60 diámetros y las cantidades de turbulencia exigen una longitud aún mayor. Estrictamente hablando, el criterio para establecer un flujo completamente desarrollado deberá ser aquel en el que la tasa de cambio de todas las cantidades medias (excepto la presión) con respecto a la coordenada en la dirección del flujo sean todas cero.
Flujos Completamente Desarrollados
a) Transición: el flujo en un tubo puede ser laminar o turbulento. El carácter del flujo viene determinado por el NRe y por la rugosidad de las paredes. Esto puede demostrarse realizando el experimento clásico de Osborne Reynolds: introducir una corriente de tinta dentro del flujo en un tubo de vidrio; para pequeños valores de la tasa de flujo, la tinta forma una linea suave. Cuando el flujo se incrementa, se alcanza un punto en el cual la tinta salta, formando un patrón dentado, indicando turbulencia.
b) Flujo Laminar: considerando flujo laminar entre paredes paralelas, donde la velocidad será máxima en el centro y nula en las paredes y la distribución de velocidades u será simétrica alrededor del eje x, se obtiene: u = 1/2μ dp/dx (y2-h2). Si el tubo es circular, u = 1/4μ dp / dx (r2 - R2).
Factor de Fricción y Pérdidas de Carga
Las pérdidas de presión ocurren en flujos internos como resultado de la fricción. Estas pérdidas pueden ocurrir en tubos rectos o ductos (pérdidas mayores) o en expansiones súbitas (válvulas, codos, etc.; pérdidas menores).
La ecuación de energía para un Volumen Control entre 2 puntos en el flujo en un conducto es
V12/2 + p1/ρ + gz1 = V22/2 + p2/ρ + gz2 + u2 - u1 - q
Llamando a (u2 - u1 - q) / g = HL
resulta:
V12/ 2g + p1 / ρg + z1 = V2 / 2g + p2 / ρg + z2 + HL
El término HL ya fue descrito y señala la pérdida de carga; por su parte, u es la energía interna especifica. HL representa el decrecimiento (pérdidas) de la energía mecánica entre los puntos 1 y 2, y en general, incluye pérdidas mayores y menores.
Para considerar las pérdidas, se procede a métodos básicamente empíricos, pues no existe forma puramente analítica para determinar estas pérdidas en flujo turbulento.
Para determinar las Pérdidas Mayores (sólo para flujo turbulento incompresible completamente desarrollado en un tubo de diámetro constante) se observa, en la última ecuación, que los cambios de presión dependen de cambios de velocidad, cambios de altura y pérdidas por fricción; para área constante, en este caso, V1 = V2 y suponiendo z1 = z2, la ecuación se reduce a HL = (p1 - p2) / ρg.
El cambio de presión depende de: (1) el diámetro del tubo D, (2) la velocidad media V, (3) la longitud L, (4) la viscosidad μ, (5) la densidad ρ y (6) la rugosidad de las paredes, K. Así, resolviendo, resultó:
Δp/ρg = HL =[f L/ D] / V2 / 2g], donde (es el factor de fricción y V2 / 2g es la altura de velocidad. Los resultados de la determinación experimental del factor de fricción se indican en el siguiente diagrama, llamado Diagrama de Moody:
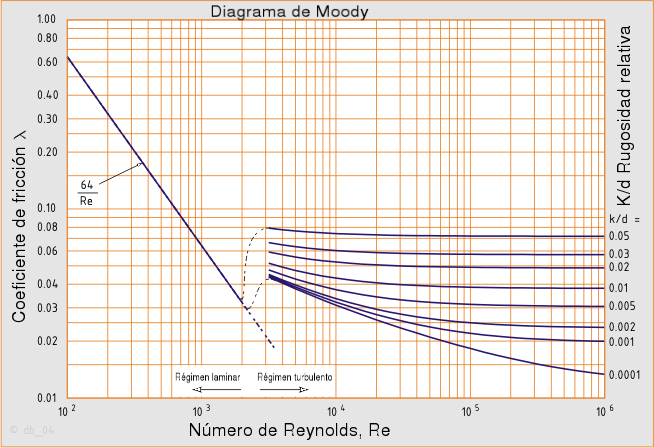
Con los datos del flujo y del conducto, se puede obtener su Número de Reynolds de tal, y por lo tanto, el régimen que desarrolla (eje horizontal). Por las características del conducto, se ubica la rugosidad relativa (eje vertical). Con la intersección de ambos valores, se determina el coeficiente de fricción. Si el régimen es laminar, se utiliza la fórmula 64 / NRe. De lo contrario, se utilizan los valores empíricos que figuran en el diagrama.
Para NRe < a 2000, el flujo es laminar y f = 64 / NRe. Para flujo laminar, en todas las tuberías y para cualquier fluido: f = 64 / NRe, con NRe máx = 2000; Para flujo turbulento no se dispone de relaciones matemáticas sencillas para obtener la variación de f con el Número de Reynolds: depende de la rugosidad y el grado de la tubería.
Para determinar las Pérdidas Menores (pérdidas en codos, válvulas y expansiones) se debe recurrir a la experimentación, esas pérdidas son: HL = KV2 / 2g, donde K es el coeficiente de pérdidas de fricción para varios tipos de pérdidas menores y están tabulados en manuales (flujo turbulento en accesorios) y V2/2g es la altura de velocidad.
Distribución de velocidades para Flujos Laminar y Turbulento:
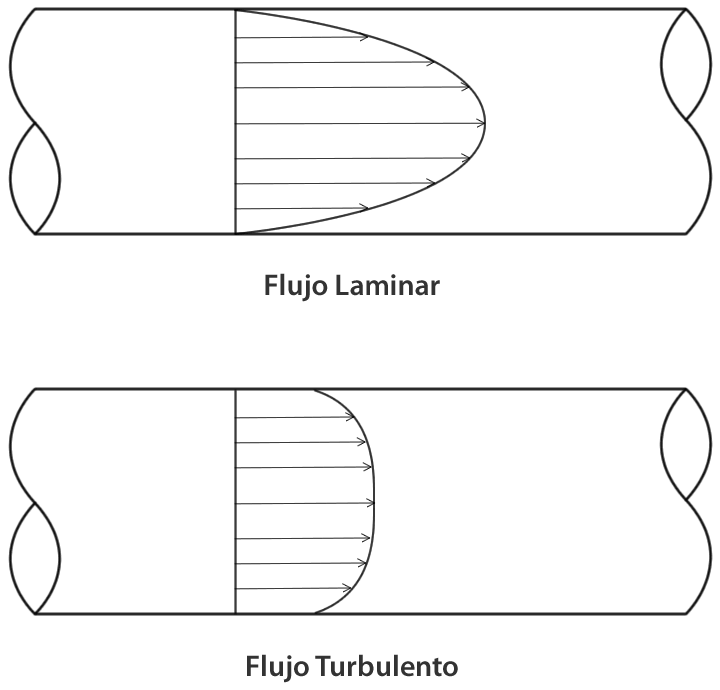
En flujo laminar, la distribución de velocidades en una sección recta seguirá la ley de
variación parabólica. La velocidad máxima tiene lugar en el eje de la tubería y es el doble de la media.
En este flujo, los módulos de las velocidades de las capas adyacentes no tienen el mismo valor. El flujo laminar está gobernado por la ley que relaciona la tensión cortante con la velocidad de deformación angular, es decir, τ = μ du/dy. La acción de la viscosidad amortigua cualquier tendencia a turbulencia.
En flujo turbulento, la distribución es más uniforme (u / umáx, = (y / /NRe)1/n); con y la
distancia de la pared, medida al centro y 1/6 < 1/n < 1/10 para 4 x 103 < NRe< 3 x 106. En el flujo turbulento, las partículas fluidas se mueven de forma desordenada en todas las direcciones, por lo cual es imposible conocer la trayectoria de una partícula individualmente. La tensión cortante en el flujo turbulento puede expresarse como, τ = ( μ + η) du/dy donde η es un factor que depende de la densidad del fluido y de las características del movimiento.
Velocidad Critica
Es la velocidad por debajo de la cual toda turbulencia es amortiguada por la viscosidad del fluido.
Pérdidas de Carga en Flujo Laminar
Fórmula de Hagan-Pousellle: Pérdida de carga =
32 μLV / γd2
donde μ es la viscosidad, L la longitud en metros, V la velocidad media, γ el peso especifico y d el diámetro en metros. En función de la viscosidad cinemática: Pérdida de carga =
32 vLV/gd2
donde L es la longitud en metros, V la velocidad media, d el diámetro en metros, v / g es la relación viscosidad / peso especifico y μ /ρ es la viscosidad cinemática
Fórmula de Darcy-Welsbach: Pérdida de carga en tuberías y ductos (m) =
fLv / d2g
donde f es el factor de fricción, L es la longitud en metros, al igual que el diámetro D y V2/2g es la altura de velocidad.