Este es un caso de modulación donde tanto las señales de transmisión como las señales de datos son analógicas y es un tipo de modulación exponencial.
En este caso la señal modulada mantendrá fija su amplitud y el parámetro de la señal portadora que variará es la frecuencia, y lo hace de acuerdo a como varíe la amplitud de la señal moduladora.
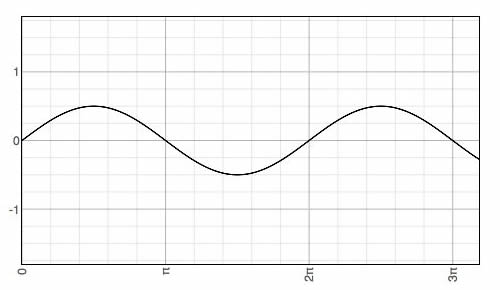
Señal Moduladora (Datos)
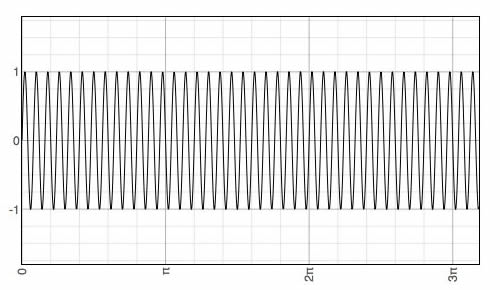
Señal Portadora
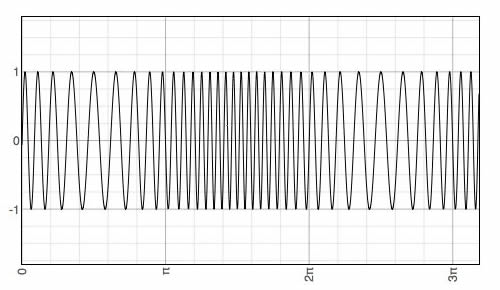
Señal Modulada
La expresión matemática de la señal portadora, está dada por:
(1) vp(t) = Vp sen(2π fp t)
Donde Vp es el valor pico de la señal portadora y fp es la frecuencia de la señal portadora.
Mientras que la expresión matemática de la señal moduladora está dada por:
(2) vm(t) = Vm sen(2π fm t)
Siendo Vm el valor pico de la señal moduladora y fm su frecuencia.
De acuerdo a lo dicho anteriormente, la frecuencia f de la señal modulada variará alrededor de la frecuencia de la señal portadora de acuerdo a la siguiente expresión
f = fp + Δf sen(2 π fm t)
por lo tanto la expresión matemática de la señal modulada resulta
vp(t) = Vp sen[2π (fp + Δf sen(2 π fm t) ) t]
Δf se denomina desviación de frecuencia y es el máximo cambio de frecuencia que puede experimentar la frecuencia de la señal portadora. A la variación total de frecuencia desde la más baja hasta la más alta, se la conoce como oscilación de portadora.
De esta forma, una señal moduladora que tiene picos positivos y negativos, tal como una señal senoidal pura, provocara una oscilación de portadora igual a 2 veces la desviación de frecuencia.
Una señal modulada en frecuencia puede expresarse mediante la siguiente expresión
Se denomina índice de modulación a 
Se denomina porcentaje de modulación a la razón entre la desviación de frecuencia efectiva respecto de la desviación de frecuencia máxima permisible.
Al analizar el espectro de frecuencias de una señal modulada en frecuencia, observamos que se tienen infinitas frecuencias laterales, espaciadas en fm, alrededor de la frecuencia de la señal portadora fp; sin embargo la mayor parte de las frecuencias laterales tienen poca amplitud, lo que indica que no contienen cantidades significativas de potencia.
El análisis de Fourier indica que el número de frecuencias laterales que contienen cantidades significativas de potencia, depende del índice de modulación de la señal modulada, y por lo tanto el ancho de banda efectivo también dependerá de dicho índice.
Schwartz desarrollo la siguiente gráfica para determinar el ancho de banda necesario para transmitir una señal de frecuencia modulada cuando se conoce el índice de modulación.
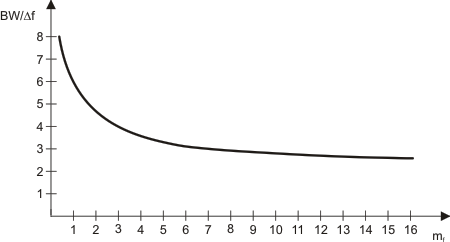
En la construcción de la gráfica se ha empleado el criterio práctico que establece que una señal de cualquier frecuencia componente, con una magnitud (tensión) menor de 1% del valor de la magnitud de la portadora sin modular, se considera demasiado pequeña como para ser significativa.
FM de banda angosta y FM de banda ancha
Al examinar la curva obtenida por Schwartz, se aprecia que para altos valores
de mf, la curva tiende a la asíntota horizontal, mientras que
para valores bajos de mf tiende a la asíntota vertical. Un estudio
matemático detallado indica que el ancho de banda necesario para transmitir
una señal FM para la cual 
, depende principalmente
de la frecuencia de la señal moduladora y es totalmente independiente de
la desviación de frecuencia. Un análisis más completo demostraría que el
ancho de banda necesario para transmitir una señal de FM, en la cual , es igual a dos veces
la frecuencia de la señal moduladora.
BW = 2 fm para
De igual manera que en AM ya a diferencia de lo que ocurre para FM con 
, por cada frecuencia
moduladora aparecen dos frecuencias laterales, una inferior y otra superior,
a cada lado de la frecuencia de la señal portadora y separadas en fm de
la frecuencia de la portadora. Dado lo limitado del ancho de banda cuando , se la denomina FM
de banda angosta, mientras que las señales de FM donde , se las
denomina FM de banda ancha.
Los espectros de frecuencia de AM y de FM de banda angosta, aunque pudieran parecer iguales, por medio del análisis de Fourier se demuestra que las relaciones de magnitud y fase en AM y FM son totalmente diferentes
En FM de banda ancha se tiene la ventaja de tener menor ruido.
En FM el contenido de potencia de las señal portadora disminuye conforme aumenta mf, con lo que se logra poner la máxima potencia en donde está la información, es decir en las bandas laterales.