Señales de transmisión digitales y señales de datos analógicas

Modulaciones de pulsos

Consiste en tomar muestras de la señal moduladora de datos a intervalos regulares, de modo que el receptor a través de dichas muestras pueda reconstruir la señal de datos original.

En modulación de pulsos la información no está contenida en toda la señal moduladora, sino que la información está codificada en forma digital mediante un muestreo adecuado. En la demodulación, en general es suficiente con detectar la existencia o no de un pulso.

En la modulación de pulsos algún parámetro de pulso varía de acuerdo a un valor muestra de la información.

Los pulsos representativos de la señal moduladora son de muy corta duración en comparación al tiempo entre ellos. Debido a esta circunstancia, la potencia transmitida se puede concentrar en ráfagas cortas, en lugar de ser enviada en forma continuada.

La modulación de pulsos es más un técnica de procesamiento de información que una modulación, puesto que no hay traslación de fase.

Muestreo

Una aproximación simple del muestreo, se consigue por medio de la operación de conmutación.

 

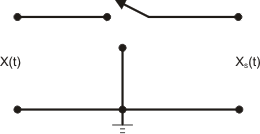
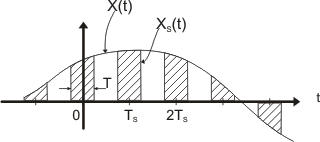
El conmutador contacta periódicamente entre 1 y 2 con una frecuencia f_s = 1/T_s, y permanece en contacto con el Terminal 1 de la señal de entrada un tiempo T, para luego estar contactado a masa el resto del tiempo T_s, A f_s se la denomina frecuencia de muestreo, siendo X_s (t) la señal modulada (muestreada).

Si llamamos S(t) a la función de conmutación (forma de variación de la conmutación), siendo al misma una secuencia periódica de pulsos de muestreo de amplitud unitaria, podemos considerar a la modulación como el producto de la señal moduladora de datos por la función S(t).

X_S(t) = X(t) S(t) (1)

Como S(t) es una función periódica de pulsos, haciendo un adecuado cambio de variables y aplicando la serie de Fourier, tenemos:

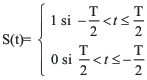
y como W₁ = WS resulta f₁ = f_S

resulta:

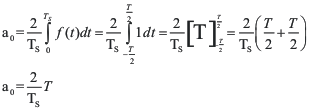
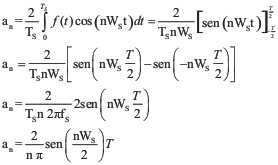
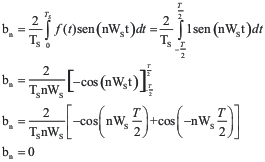
Llamando:

a₀=2C₀ y a_n=2C_n

reemplazando en el desarrollo de Fourier, resulta:

(2)

reemplazando (2) en (1) tenemos:

Si X(t) = sen 2pft reemplazando resulta

como sen x cos y = ½ [sen (x+y) + sen (x-y)], resulta

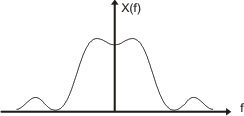
La expresión anterior indica que la operación de muestreo ha dejado al espectro del mensaje de datos intacto (primer término), repitiéndolo periódicamente en un espaciamiento f_s.

Si el ancho de banda de la señal de datos (el ancho de banda necesario para que la señal recibida se corresponda con la señal emitida, o sea para que la deformación sea mínima) es W, para que las bandas laterales no se solapen, la frecuencia de muestreo f_s, deber ser como mínimo:

f_s - W = W de donde obtenemos la frecuencia de muestreo mínima

f_s = 2 W

a esta frecuencia se la denomina velocidad de Nyquist y una demostración más rigurosa se obtiene por medio de la teoría del muestreo.

Por lo tanto, la velocidad de muestreo debe ser f_s > 2W

Y por lo tanto el período del muestreo resulta T_s = 1 / f_s = 1/2W

Y cuando esto satisface, en el receptor se filtra X_s(t) por medio de un filtro pasabajos, obteniéndose a la salida del mismo una señal que será proporcional a X(t), resultando de esta la recuperación de la señal de datos.

Si f_s < 2W, la señal obtenida no responde exactamente a la señal muestreada, debido al efecto de interferencia de las coles espectrales (aliasing).

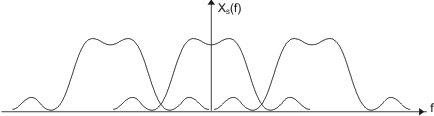
Hay dos técnicas de modulación de pulsos

• Modulación analógica de pulsos
• Modulación de pulsos codificados