Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
En este artículo, valiéndonos del hecho de que la dilatación gravitacional del tiempo se manifiesta a través de los cambios de módulo o dirección de la velocidad, aprovechando esto se describe entonces de manera dual con una misma transformación de Cuadri-Lorentz, como el tiempo se dilatada gravitacionalmente actuando sobre la misma magnitud vectorial de la velocidad. Para lograr esto hemos tenido que remplazar a la clásica contracción de Lorentz, estableciendo pues unas leyes de transformaciones distintas y acordes a las densidades de masa y energía, que necesitaron entonces utilizar una nueva relación de energía-momento, relación que hemos llamado Cuadri-contracción de Cuadri-Lorentz. En este trabajo se demuestra de manera general que: la dilatación por velocidad y gravedad del tiempo, ocurre a cualquier velocidad y aceleración en la naturaleza, generalmente imperceptible.
Palabras claves: Dilatación del tiempo, Dilatación gravitacional del tiempo, Contracción de Lorentz, Relatividad General, Gravedad Cuántica, Gravitón, Energía Potencial Gravitatoria.
Abstract
In this article, being worth to us of the fact that the gravitational expansion of the time pronounces through the changes of module or direction of the speed, taking advantage of this is described then of dual way with a same transformation of Cuadri-Lorentz, like the expanded time gravitationally acting itself on the same vectorial magnitude of the speed. In order to obtain this we have had to replace to the classic contraction of Lorentz, establishing because laws of transformations different and agreed to the densities of mass and energy, that needed then to use a new relation of energy-moment, relation that we have called Cuadri-contraction of Cuadri-Lorentz. In this work one demonstrates of general way that: the expansion by speed and gravity of the time happens at any speed and acceleration in the nature, generally imperceptible.
Key Words: Expansion of the Time, gravitational Expansion of the Time, Contraction of Lorentz, General Relativity, Quantum Gravity, Graviton, Gravitational Potential Energy.
1. Introducción
La dilatación del tiempo es el fenómeno predicho por la teoría de la relatividad, por el cual un observador observa que el reloj de otro (un reloj físicamente idéntico al suyo) está marcando el tiempo a un ritmo distinto que el que mide su reloj. Esto se suele interpretar normalmente como que el tiempo se ha ralentizado para el otro reloj, pero eso es cierto solamente en el contexto del sistema de referencia del observador. Localmente, el tiempo siempre está pasando al mismo ritmo. El fenómeno de la dilatación del tiempo se aplica para cualquier proceso que manifieste cambios a través del tiempo.
En las teorías de le relatividad de Albert Einstein la dilatación temporal del tiempo se manifiesta en dos circunstancias:
En la teoría de la Relatividad Especial, relojes que se mueven con respecto a un sistema de referencia inercial (el hipotético observador inmóvil) deberían funcionar más despacio. Este efecto está descrito por las transformaciones de Lorentz en la relatividad especial para observadores que siempre se acercan.
En la relatividad especial, la dilatación del tiempo es recíproca: vista como dos relojes que se mueven acercándose uno con respecto al otro, será el reloj de la otra parte aquél en el que el tiempo se dilate.
Las formulas actuales para determinar la dilatación del tiempo en la relatividad especial es:
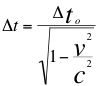
Donde Δt0 es el intervalo temporal entre dos eventos co-locales para un observador en algún sistema de referencia inercial (por ejemplo el número de tic-tac que ha hecho su reloj), Δt es el intervalo entre los dos mismos eventos, tal y como lo mediría otro observador moviéndose inercialmente con velocidad v con respecto al primer observador, v es la velocidad relativa entre los dos observadores, c es la velocidad de la luz.
En la teoría de la Relatividad General, relojes que tengan potenciales gravitatorios menores, como aquellos que se encuentran cerca de un planeta, marcan el tiempo más lentamente.
En contraste, la dilatación gravitacional del tiempo (como es considerada en la relatividad general) no es recíproca: un observador en lo alto de una torre observará que los relojes del suelo marcan el tiempo más lentamente, y los observadores del suelo estarán de acuerdo. De esta manera la dilatación gravitacional del tiempo es común para todos los observadores estacionarios, independientemente de su altitud.
De acuerdo con la relatividad general los sistemas acelerados, tales como de marco de referencia acelerado tal como un dragster (vehículo de carreras especial donde impera la potencia y velocidad máxima alcanzada) o un transbordador espacial también experimentarían una dilatación del tiempo similar a la que acontece en un campo gravitatorio. Igualmente en sistemas de referencia giratorios tales como un carrusel y norias aparecerá dilatación del tiempo similar a la dilatación gravitacional del tiempo como efecto de sus giros. Es interesante notar de todas maneras, que en general los sistemas de referencia acelerados a pesar de la dilatación temporal no se dan sobre espacios-tiempo "curvados". De hecho el espacio-tiempo percibido por una partícula dentro de un sistema de referencia giratorio dentro del espacio de Minkowski es plano (es decir, el tensor de curvatura es nulo aunque los símbolos de Christoffel no sean nulos). En cualquier caso cualquier tipo de carga-g en un sistema de referencia no-inercial contribuye a la dilatación gravitacional del tiempo.
En física se considera Reposo a un estado de movimiento rectilíneo uniforme tanto del observador como del sistema observado, estado en el cual la velocidad es nula entre ellos. El reposo sólo existe con respecto a un determinado punto de referencia. En el universo no existe el reposo absoluto. En este trabajo el Reposo se mantendría en la eventualidad de que el observador rote sobre su propio oje o el objeto observado rote alrededor del observador y viceversa.
En física, un observador es cualquier ente capaz de realizar mediciones de magnitudes físicas de un sistema físico para obtener información sobre el estado físico de dicho sistema.
Por "abuso de lenguaje" también se denomina observador a la descripción matemática de uno de esos entes capaces de hacer medidas. Dados dos observadores diferentes, un problema fundamental es establecer las leyes de transformación necesarias para relacionar las medidas de ambos observadores.
Los observadores en mecánica clásica tienen dos propiedades fundamentales: Primero el tiempo es absoluto, por que tiene el mismo valor invariante para todos los observadores independiente de su estado de movimiento. Segundo, pueden tratarse discrecionalmente al observador y al sistema físico observado es decir, que cualquiera que sea la magnitud física observada en el proceso de medición no altera el estado físico.
En mecánica relativista, de las dos propiedades fundamentales de los observadores en la mecánica clásica: tiempo absoluto y discrecionalidad de la medida, solo se mantiene la segunda, ya que cada observador tiene su tiempo propio.
En mecánica relativista el observador de una región del espacio-tiempo, viene caracterizado por una sección del fibrado de bases ortonormales del espacio tangente a cada punto del espacio-tiempo curvo. Así un observador sería una asignación a cada punto del espacio tiempo de cuatro campos vectoriales continuos mutuamente ortogonales, que representarían los "ejes de coordenadas" usados para ese punto. Matemáticamente estos campos vectoriales forman un marco móvil. La condición de que el observador sea físicamente realizable, mediante instrumentos y aparatos de medida, es que uno de estos campos vectoriales sea para todo punto del espacio-tiempo un vector temporal. Un observador por tanto podría representarse sobre una región con coordenadas xμ como:
![]()
Donde:
![]()
La objetividad física del espacio-tiempo, o más propiamente intersubjetividad de las medidas, implica que al ser observado un mismo fenómeno físico por diferentes observadores las medidas realizadas por estos deben ser relacionables por reglas fijas, conocidas como leyes de transformación acordes a si la magnitud física es de tipo escalar, vectorial o propiamente tensorial.
En mecánica cuántica, de los dos supuestos fundamentales de los observadores de la mecánica clásica, el de discrecionalidad de la medida resulta inaceptable, en cambio el del tiempo absoluto es usado en mecánica cuántica no relativista, pero no es aceptable en mecánica cuántica relativista.
El resultado de una magnitud física no tiene que tener un valor determinado y fijo para un observador. El resultado de una medida es una variable aleatoria que aunque su distribución de probabilidad generalmente sí es conocida además durante el proceso de medida, el sistema experimenta una evolución no determinista e impredictible.
Un sistema de referencia o marco de referencia es un conjunto de convenciones usadas por un observador para poder medir la posición y otras magnitudes físicas de un objeto o sistema físico en el tiempo y el espacio.
En mecánica clásica frecuentemente se usa el término de sistema de referencia para referirse a un sistema de coordenadas ortogonales para el espacio euclídeo y dados dos sistemas de coordenadas de ese tipo, existe un giro y una traslación que relacionan las medidas de esos dos sistemas de coordenadas.
En física clásica un sistema de referencia se define por un par (P, E), donde el primer elemento P' es un punto de referencia arbitrario, normalmente perteneciente a un objeto físico, a partir del cual se consideran las distancias y las coordenadas de posición. El segundo elemento E es un conjunto de ejes de coordenadas. Los ejes de coordenadas tienen como origen de coordenadas en el punto de referencia (P), y sirven para determinar la dirección y el sentido del cuerpo en movimiento (o expresar respecto a ellos cualquier otra magnitud física vectorial o tensorial).
Un tercer elemento es el origen en el tiempo, un instante a partir del cual se mide el tiempo. Este instante acostumbra a coincidir con un suceso concreto. En cinemática el origen temporal coincide habitualmente con el inicio del movimiento que se estudia.
Estos tres elementos: punto de referencia, ejes de coordenadas y origen temporal, forman el sistema de referencia. Para poder utilizar un sistema de referencia, sin embargo, se necesitan unas unidades de medida que nos sirvan para medir. Las unidades son convencionales y se definen tomando como referencia elementos físicamente constantes. A un conjunto de unidades y sus relaciones se le llama sistema de unidades. En el Sistema Internacional de Unidades o S.I., se utiliza el metro como unidad del espacio y el segundo como unidad del tiempo.
En mecánica relativista se refiere el término “sistema de referencia” usualmente al conjunto de coordenadas espacio-temporales que permiten identificar cada punto del espacio físico de interés y el orden cronológico de sucesos en cualquier evento, más formalmente un sistema de referencia en relatividad se puede definir a partir de cuatro vectores ortonormales (1 temporal y 3 espaciales).
En mecánica, un sistema de referencia inercial es un sistema de referencia en el que las leyes del movimiento cumplen la conservación del momento lineal. El término aparece principalmente en mecánica newtoniana donde los sistemas inerciales son precisamente aquellos en los que se cumplen las leyes de Newton.
Fuera de la mecánica newtoniana, como en la Teoría de la Relatividad Especial también se pueden definir sistemas inerciales. Aunque en relatividad especial la caracterización matemática no coincide con la que se da en mecánica newtoniana, debido a que la segunda ley de Newton tal como la formuló Newton no se cumple en relatividad.
En mecánica clásica y teoría de la relatividad especial, los sistemas inerciales pueden ser caracterizados de forma muy sencilla, un sistema inercial es aquel en el que los símbolos de Christoffel obtenidos a partir de la función lagrangiana se anulan.
En un sistema inercial no aparecen fuerzas ficticias para describir el movimiento de las partículas observadas, y toda variación de la trayectoria tiene que tener una fuerza real que la provoca.
Siendo rigurosos podría argumentarse que los sistemas de referencia inerciales no existen, o al menos no en nuestro entorno, pues la Tierra gira sobre sí misma y también alrededor del Sol, y éste a su vez lo hace respecto al centro de la Vía Láctea. Sin embargo, con objeto de simplificar los problemas, normalmente se considerarán como inerciales sistemas que en realidad no lo son, siempre que el error que se cometa sea aceptable. Así, para muchos problemas resulta conveniente considerar la superficie de la Tierra como un sistema de referencia inercial.
Dado un sistema de referencia inercial, un segundo sistema de referencia será no inercial cuando describa un movimiento acelerado respecto al primero. La aceleración del sistema no inercial puede deberse a: a) un cambio en el módulo de su velocidad de traslación (aceleración lineal). b) Un cambio en la dirección de la velocidad de traslación (un movimiento de giro alrededor de un sistema de referencia inercial) c) Un movimiento de rotación sobre si mismo d) Una combinación de algunos de los anteriores.
Ahora vamos a tomar y traer a colación recordando la conclusión de la nueva relación de energía-momento con cuadri-Lorentz incluido, donde se deja identificado y especificado que para una partícula que precisamente se aleja del observador, se describe su movimiento con la siguiente ecuación número uno (1):
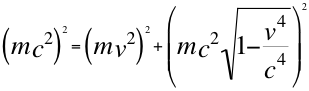 (1)
(1)
Donde m es la masa invariante de la partícula observada, v es la velocidad resultante de la partícula en dirección de retiro y contraria al observador y c es la velocidad de la luz.
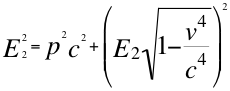 (2)
(2)
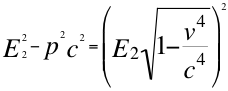 (3)
(3)
Donde E2es la energía invariante del objeto observado equivalente a la masa también invariante de la respectiva partícula observada, p es la cantidad de movimiento de retiro en dirección contraria al observador, v es la velocidad resultante de la partícula en sentido también contrario al observador y c la velocidad de la luz en vacío.
![]() (4)
(4)
Donde E2 es la energía invariante de la partícula que se aleja del observador equivalente a su respectiva masa también invariante y que en este caso coincide perfectamente con el valor de la energía total del movimiento, Ec es la energía cinética de dicha partícula en dirección contraria al observador y Ep es la energía potencial gravitatoria relativa asociada tanto al grado de separación como el movimiento del objeto observado y que tiene dirección perpendicular a la recta que une al objeto observado y el observador.
![]() (5)
(5)
![]() (6)
(6)
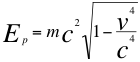 (7)
(7)
También aparece la presentación de la nueva formulación matemática de la cantidad de movimiento para observadores que se alejan del objeto en movimiento:
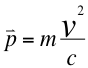 (8)
(8)
Donde p es la Cantidad de movimiento de alejamiento en dirección contraria al observador, m es la masa invariante de la partícula observada, v es la velocidad resultante en dirección contraria de retiro de la partícula y c es la velocidad de la luz.
También dejamos presente en esta introducción que la nueva relación de energía-momento con cuadri-Lorentz incluido, se puede aplicar también al movimiento de una partícula pero en esta ocasión precisamente es un objeto que se acerca al observador, se describe ese movimiento de acercamiento con la siguiente ecuación número nueve (9):
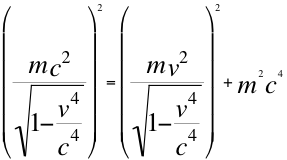 (9)
(9)
Donde m es la respectiva masa invariante de la partícula que se acerca al observador, v es la velocidad resultante de la partícula dirigida de acercamiento hacia el observador y c es la velocidad de la luz.
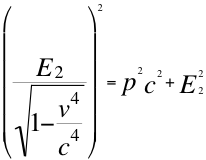 (10)
(10)
Donde E2 es la energía invariante del objeto observado equivalente a la masa también invariante de la respectiva partícula observada que se acerca, p la cantidad de movimiento dirigida hacia el observador, v la velocidad resultante de la partícula en dirección hacia el observador y c la velocidad de la luz en el vacío.
![]() (11)
(11)
Donde Ep es la energía potencial gravitatoria relativa que en este caso coincide con la energía total involucrada en el movimiento de la partícula que se acerca al observador, Ec es la energía cinética de dicha partícula en dirección hacia el observador y E2 es la energía invariante de dicha partícula que se observa correspondiente a su masa también invariante de la partícula y es perpendicular a la recta que une al observador y el objeto observado.
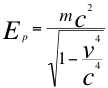 (12)
(12)
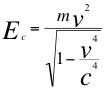 (13)
(13)
![]() (14)
(14)
Donde m es la masa invariante de la partícula observada, v es la velocidad resultante de la partícula en dirección hacia el observador y c es la velocidad de la luz.
Finalmente en esta introducción vamos a dejar recordado a la formulación matemática de p o cantidad de movimiento pero, para una partícula que precisamente se acerca al observador:
 (15)
(15)
Donde p es la cantidad de movimiento dirigida hacia el observador, m es la masa invariante de la partícula observada, v es la velocidad resultante de la partícula dirigida hacia el observador y c es la velocidad de la luz.
La energía cinética de un cuerpo, es una energía que surge en el fenómeno del movimiento y como cualquier magnitud física que sea función de la velocidad, la energía cinética de un objeto no solo depende de la naturaleza interna de ese objeto, también depende de la relación entre el objeto y el observador (en física un observador es formalmente definido por una clase particular de sistema de coordenadas llamado sistema inercial de referencia). Magnitudes físicas como ésta son llamadas invariantes. La energía cinética esta co-localizada con el objeto y atribuido a ese campo gravitacional.
2. Desarrollo del Tema.
Queremos partir en este ensayo, de una energía cinética descrita de manera totalmente general, que dependa de una relación más estrecha entre el objeto y los sistemas de referencia materiales totalmente generales. No queremos partir nuestro artículo, de una energía cinética definida simplemente como aquel trabajo absoluto que necesita realizar cualquier observador, para acelerar o desacelerar hasta o desde una velocidad absoluta y en cualquier dirección, a una determinada cantidad de masa.
Einstein había concebido la teoría de la Relatividad Especial como una teoría aplicable solo a sistemas de referencia inerciales, no por que no fuera apta para el estudio de sistemas acelerados tangencialmente en un espacio tiempo plano, la insatisfacción de Einstein era precisamente por que las leyes de transformación de Lorentz como principio especial en la Relatividad Especial, no eran competentes para transformar relativamente las diferentes densidades de masa y energía para todos los observadores de un espacio-tiempo curvado.
Entendiendo el Reposo como un estado de movimiento rectilíneo uniforme en trayectorias paralelas tanto del observador como del sistema observado, estado en el cual la velocidad es nula entre ellos. Cuando se rompe ese estado de reposo aparece el movimiento relativo entre observadores.
Dilatación del Tiempo por Velocidad.
Partiendo de la ecuación número uno (1) de este trabajo, que representa la ecuación de movimiento descrita por un observador sin gravedad que se aleja y se ubica a la retaguardia del objeto que se mueve, podría ser incluso hasta el mismo observador el ente que probablemente origina el movimiento del objeto:
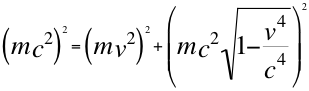 (1)
(1)
Donde m es la masa invariante de la partícula u objeto observado, v es la velocidad resultante de la partícula en dirección de retiro y contraria al observador y c es la velocidad de la luz.
En esta anterior ecuación número uno (1) se identifica pues a la energía cinética de un cuerpo, expresada en la siguiente ecuación número seis (6), que no manifiesta dilatación del tiempo por velocidad para un observador sin gravedad que se aleja del objeto:
![]() (6)
(6)
Donde m es la masa invariante de la partícula u objeto observado, v es la velocidad resultante de la partícula en dirección de retiro y contraria al observador y Ec es la energía cinética.
También observamos en la anterior ecuación número uno (1), como el cuarto vector contrae a la energía potencial gravitatoria del objeto observado, es decir el objeto le pesa menos al observador que se aleja, decrece al compas de la velocidad, tal como se corrobora en la siguiente ecuación número (7):
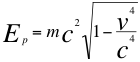 (7)
(7)
Donde m es la masa invariante de la partícula u objeto observado, v es la velocidad resultante de la partícula en dirección de retiro y contraria al observador, Ep es la energía potencial gravitatoria y c es la velocidad de la luz.
Ahora si el análisis de la energía cinética y potencial gravitatoria de ese mismo cuerpo estudiado en la ecuación uno (1), seis (6) y siete (7), lo hace y los siente es un observador sin gravedad a quien el objeto se le acerca, entonces es descrito con la siguiente ecuación número nueve (9):
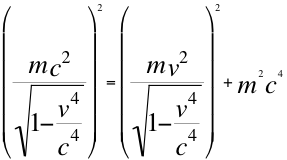 (9)
(9)
Donde m es la respectiva masa invariante de la partícula que se acerca al observador, v es la velocidad resultante de la partícula dirigida de acercamiento hacia el observador y c es la velocidad de la luz.
En esta anterior ecuación número nueve (9) se identifica pues que la energía cinética y potencial gravitatoria del mismo objeto que se acerca, se incrementa relativa y proporcionalmente para un observador sin gravedad que se acerca, el objeto o cuerpo que se acerca le pesa más al observador, incrementado por efectos precisamente de la identificada “dilatación del tiempo por velocidad”, expresada mejor en la siguientes ecuaciones número doce (12) y trece (13):
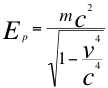 (12)
(12)
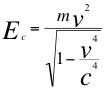 (13)
(13)
Donde m es la masa invariante de la partícula u objeto observado, v es la velocidad resultante de la partícula en dirección hacia el observador, Ep es la energía potencial gravitatoria, Ec es la energía cinética y c es la velocidad de la luz.
Se puede decir que la dilatación o no del tiempo entre dos observadores, vista como dos relojes que se mueven es reciproca entre si, es decir: si se va a dilatar el tiempo en uno de ellos cuando se acerca pues lo hacen también en el otro y, si no se va a dilatar el tiempo en uno de ellos cuando se alejan tampoco lo hace en el otro, todo dependería de si los relojes se acercan o se alejan. Si los relojes se alejan algún grado, el tiempo no se dilata por la velocidad pero, si los relojes se acercan en alguna medida el tiempo se dilata por velocidad, simplemente de manera reciproca.
Quiere decir que la cuadri-contracción de cuadri-Lorentz sería el factor que remplazaría a las transformaciones clásicas de Lorentz:
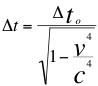 (16)
(16)
Donde Δt0 es el intervalo temporal entre dos eventos co-locales para un observador en algún sistema de referencia inercial (por ejemplo el número de tic-tac que ha hecho su reloj), Δt es el intervalo entre los dos mismos eventos, tal y como lo mediría otro observador que se acerca moviéndose inercialmente con velocidad v con respecto al primer observador, v es la velocidad relativa entre los dos observadores, c es la velocidad de la luz.
 (16a)
(16a)
Finalmente un ejemplo sencillo y práctico de dilatación por velocidad del tiempo, es el lanzamiento de una pelota por una persona a gran velocidad uniforme y otra que la recibe. La energía cinética de la pelota según el observador que la recibe es mayor del que lo lanza, debido a la dilatación del tiempo por velocidad.
Dilatación Gravitacional del Tiempo.
La dilatación gravitacional del tiempo se debe considerar de manera adicional, al estudio de la dilatación del tiempo por velocidad y si los observadores cuentan con gravedad. Vemos que se manifiesta en marcos de referencias acelerados y es por eso que en virtud del principio de equivalencia ocurra en el campo gravitatorio de objetos masivos. Sistemas acelerados tales como un dragster (vehículo de carreras especial donde impera la potencia y velocidad máxima alcanzada) o un transbordador espacial, también experimentarían una dilatación del tiempo similar a la que acontece en un campo gravitatorio.
Sistemas de referencia giratorios tales como un carrusel y norias aparecerá dilatación temporal, similar a la dilatación gravitacional del tiempo como efecto de su giros. Este último hecho es importante resaltar por que los cambios son en la dirección del vector velocidad aunque el módulo se conserve constante.
Cuando un objeto se acerca a un observador provisto de gravedad, entonces se manifiesta una respectiva dilatación por velocidad del tiempo medida por el observador que se acerca al objeto y además, como se presenta una discrepancia en el paso del tiempo propio en diferentes posiciones y niveles definidas del espacio-tiempo del campo gravitatorio, entonces habrá una aceleración gravitatoria que podrá ser positiva o negativa de acuerdo al campo gravitatorio. En la siguiente ecuación número diez y siete (17) se presenta una manera de calcular la energía cinética producto de los efectos de la dilatación del tiempo por velocidad y gravedad que podría ser negativo por efectos del campo emisor de más intensidad que el receptor y que explica el experimento de Pound y Rebka.
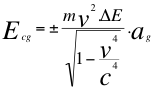 (17)
(17)
Donde m es la masa invariante de la partícula u objeto observado, v es la velocidad resultante de la partícula en dirección hacia el observador, Ecg es la energía cinética que es producto de la dilatación gravitacional del tiempo, ΔE es un factor de dilatación adimensional del tiempo, ag es la aceleración gravitatoria y c es la velocidad de la luz.
 (17a)
(17a)
Cuando la aceleración no sea originada por un campo gravitatorio, si no que sería una aceleración tales como un dragster o sistemas giratorios como un carrusel y norias aparecerá dilatación del tiempo con cualquier aceleración.
 (17b)
(17b)
Donde m es la masa invariante de la partícula u objeto observado, v es la velocidad resultante de la partícula en dirección hacia el observador, Ecg es la energía cinética que es producto de la dilatación gravitacional del tiempo, ΔE es un factor de dilatación adimensional del tiempo, a es la aceleración y c es la velocidad de la luz.
Igualmente sucede con el cuarto vector que dilata el tiempo para que la aceleración actúe incrementando la energía potencial gravitatoria o sea, el ritmo de incremento de la masa gravitatoria del objeto que se acerca. Es decir el peso del objeto iría aumentando a un ritmo mayor según su aceleración expresada en la siguiente ecuación número diez y ocho (18):
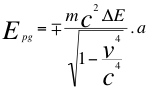 (18)
(18)
Donde m es la masa invariante de la partícula u objeto observado, v es la velocidad resultante de acercamiento de la partícula en dirección hacia el observador, Epg es la energía potencial gravitatoria que es producto de la dilatación gravitacional del tiempo, ΔE es un factor de dilatación adimensional del tiempo, a es la aceleración y c es la velocidad de la luz.
La dilatación gravitatoria del tiempo se le podría asignar unidades que mediría en unidades de energía por metros sobre segundo al cuadrado:
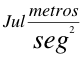 (19)
(19)
3. Conclusiones.
La gran conclusión de este trabajo es la denominada “Relatividad General formulada sin usar los clásicos tensores de Einstein” en sus dos grandes grados de libertad de elección en cuanto así el objeto observado se acerca o se aleja del observador, expresados en la Cuadri-Lorentz:
A)-La ecuación número uno (1), corresponde a la nueva relación de energía-momento que describe el movimiento del campo gravitatorio de un objeto que se aleja del observador:
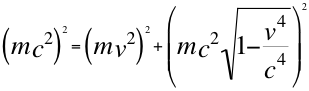 (1)
(1)
Donde m es la masa invariante de la partícula observada, v es la velocidad resultante de la partícula en dirección de retiro y contraria al observador y c es la velocidad de la luz.
B)-La ecuación número nueve (9), corresponde a la relación que describe el movimiento de un objeto que se acerca al observador:
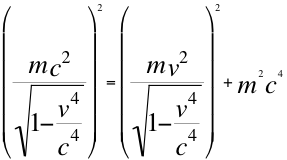 (9)
(9)
Donde m es la respectiva masa invariante de la partícula que se acerca al observador, v es la velocidad resultante de la partícula dirigida de acercamiento hacia el observador y c es la velocidad de la luz.
C)-Otra gran conclusión de este trabajo es la unificación evidente de la relatividad especial pero modificada, con la relatividad general.
D)-Nos parece apropiado concluir que el espacio cuadrimensional de la relatividad especial también es curvo, igual que el de la relatividad general, aunque no sea apreciable esa curvatura en el estudio de la radiación electromagnética con la contracción de Lorentz y la masa-energía como escalar.
E)-Es imposible dejar de comparar este trabajo con la reconocida ecuación del campo de Einstein y aprovechamos para resaltar coincidencias con unos puntos aclarados por el físico Alemán. Aquí podemos decir que la Relatividad General sin usar los tensores clásicos de Einstein describe con claridad también, como la materia crea gravedad e inversamente, como la gravedad afecta concentrando en un punto preciso a la materia. Este trabajo jamás contradice la curvatura del espacio tiempo y es mas, describe además cómo el espacio se curva también en la relatividad especial.
F)-El proceso físico de la mecánica cuántica denominado como el colapso de función de onda cuando se hace una observación/medición de un sistema en una región, entonces la función de onda varía repentinamente. Aquí en este trabajo interpretamos que la función onda sufre la curvatura del espacio por el simple hecho de estar ante un observador con masa, ya que solo su presencia altera la métrica del espacio tiempo.
G)-Una de las grandes conclusiones de este trabajo es presentar a la comunidad académica la ecuación general de la Relatividad General:
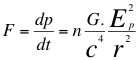 (20)
(20)
Donde F es la fuerza de atracción mutua, pes la cantidad de movimiento, G es la contante de gravitación universal, nes la relación en reposo orbital entre E1/E2, Ep es la energía potencial gravitatoria relativa asociada tanto al grado de separación como al movimiento relativo del objeto observado, c es la velocidad de la luz en el vacío y r es la distancia que hay entre el centro de gravedad del observador central y del objeto observado, E1y E2son las respectivas energías invariantes correspondientes a las respectivas masas también invariantes de observador y objeto observado.
H)-La gran conclusión de este trabajo además de los anteriores es la ratificación del desplazamiento de la contracción de Lorentz por la Cuadri-Lorentz en la siguiente ecuación número diez y seis a (16a):
 (16a)
(16a)
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
[15] http://www.monografias.com/trabajos-pdf2/matematicas-energia-cinetica-potencial-movimiento/matematicas-energia-cinetica-potencial-movimiento.pdf
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
[44] http://www.monografias.com/usuario/perfiles/pico_jimenez_heber_gabriel
[45] http://www.monografias.com/usuario/perfiles/pico_jimenez_heber_gabriel/monografias
[46] http://www.monografias.com/usuario/perfilprivado/monografias/
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.