Azimuthal quantum of the hydrogen number
Por Heber Gabriel Pico Jiménez MD
Resumen
Este artículo secamente intenta romper y acabar con el paradigma arbitrario de asignar en los estudios electrónicos del átomo, el valor condicional de cero (0) al subnivel s de energía. Ha sido una convención restrictiva y contradictoria que se ha vuelto regla oscureciendo en sí la existencia del electrón y solo lo deja que opere en la imaginación y en las probabilidades de su presencia. Sin embargo, dándole el valor convencional de uno (1) al subnivel s en este estudio electrónico del átomo, jamás se negarían los principios de la mecánica cuántica al contrario, le soltaría las manos y la facultaría para utilizar mejores herramientas porque surgirían ventajas por ejemplo, el segundo número cuántico entero haría parte directa del cálculo de la energía del electrón ya que el tercer número cuántico m dejaría de ser 2l+1 pasando a ser 2l-1 además, se conseguirían construcciones matemáticas de origen polielectrónicos, preparadas para tener en cuenta con sentido estricto, la correlación entre electrones y la antisimetría exigida por la estadística de Fermi. Además sería mucho más fácil involucrar en los distintos subniveles de energía, los efectos prácticos de la interacción espín-orbita, consistentes en que los electrones que tienen distintos valores en el tercer número cuántico, también ostentan distintas energías debidas a los efectos que producen sobre ellos el momento magnético del núcleo.
Palabras claves: Electrón, Orbital electrónico.
Abstract
This article dryly tries to break and put an end to the arbitrary paradigm assign in the electronic studios of the atom, the conditional value of zero (0) to the sublevel s of energy. It has been a restrictive and contradictory Convention which has become rule obscuring the existence of the electron itself and leaves it only to operate in the imagination and the chances of their presence. However, giving the conventional value of one (1) to the sublevel s in this electronic survey of the atom, they would never refuse the principles of quantum mechanics to the contrary, it soltaría the hands and you allow it to use better tools because there would be advantages for example, the second integer quantum would direct part of the angular momentum of the electron as the third quantum number m would be 2l+1 became 2l-1 additionyou would get mathematical constructions of orbital origin, prepared with strict sense to take into account the correlation between electrons and the antisymmetry demanded by Fermi statistics. Would also be much easier to involve in various sublevels of energy, the practical effects of the interaction of spin - orbit, consistent in that the electrons that have different values in the third quantum number, also hold different energies due to the effects that produce the magnetic moment of the nucleus upon them.
Keywords: Electron, Orbital Electronic.
1. Introducción
En base a los artículos de Inflación cuántica1,2 publicados recientemente, en donde se demuestra que el tiempo se contrae dentro del átomo a medida que el radio de mismo se reduce. Este postulado concuerda con la expansión del universo y con el problema de la medida en la mecánica cuántica.
Además presentamos las relaciones de los dos trabajos anteriores de donde partirá el desarrollo de este artículo. Aquí en estos trabajos se omite utilizar la relación clásica de la energía del electrón utilizada por Bohr pero, desarrollamos toda la matemática de este trabajo a partir del momento angular del electrón sin hacer uso de esa relación clásica de la energía.
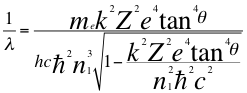 (1)
(1)
Donde λ es la longitud de onda del electrón, h es la constante de Planck, me es la masa del electrón, n1 es el primer número cuántico entero, k es la constante de coulomb, Z es el número atómico, e es la carga del electrón y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y ħ es la constante reducida de Planck.
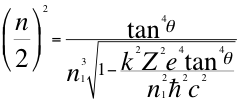 (2)
(2)
Donde n es un número que podía ser no entero y representa a la relación total presente entre el ángulo y los números cuánticos enteros del electrón, ħ es la constante reducida de Planck, n1 es el primer número cuántico entero, k es la constante de coulomb, Z es el número atómico, e es la carga del electrón y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.
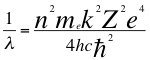 (3)
(3)
Donde λ es la longitud de onda del electrón, h es la constante de Planck, me es la masa del electrón, k es la constante de coulomb, Z es el número atómico, e es la carga del electrón, n es un número que podía ser no entero y representa a la relación total presente entre el ángulo y los números cuánticos enteros del electrón y ħ es la constante reducida de Planck.
Por eso en la explicación teórica que hace Bohr de la prueba fenomenológica de Balmer, donde solo dobla el número n no entero.
2. Desarrollo del Tema.
En base a los artículos de Inflación cuántica1,2 publicados recientemente, en donde se demuestra que el tiempo se contrae a medida que el radio del átomo se reduce. Este postulado concuerda con la expansión del universo,
El primer número cuántico entero divide por niveles al radio de todo el átomo. Los valores del primer número cuántico corresponden al valor del nivel energético que es el más determinante en la totalidad de la energía del electrón. Los valores de este número varían entre 1 y el infinito. El primer número cuántico entero históricamente ha sido considerado como el único responsable de sostener a todo el peso del momento angular, cuestión que no coincide ni siquiera en el hidrogeno.
En el cálculo de la energía fundamental del electrón la relación de la tangente del ángulo teta (θ) elevada a la cuatro, entre el factor de dilatación de la velocidad orbital del electrón, es igual a n2/4 que representaría de manera resumida en el hidrogeno o cualquier átomo a la relación de todos los número cuánticos. Pero esta n no es individualmente el primero, el segundo, el tercero ni el cuarto número cuántico, n es un número que resulta originarse de la relación matemática del momento angular del electrón donde participan el ángulo y todos los números cuánticos por tanto, para poder distinguirlo de él al primer número cuántico lo identificamos como n1.
De cada nivel que previamente dimensiona e identifica n1 como primer número cuántico, de manera interna, un segundo número cuántico se encarga de irlo dosificando cuánticamente. A pesar de que este segundo número cuántico entero l indica la forma del orbital, en este trabajo se logra identificar con él a la cantidad de energía del respectivo subnivel donde orbita el electrón. Los valores de este segundo número varían desde uno 1 hasta el mismo valor que alcanza el respectivo nivel de energía n1. No decimos n para que no correr el riesgo de confundirlo con él n que representa la intensidad total en el momento angular, por lo tanto n es el número total que representaría la relación que tienen todos los niveles y subniveles energéticos del momento angular del electrón y que incluso podría no ser exactamente un número entero. Partiendo de que el valor del subnivel llega hasta n1 y vamos a referirnos a un electrón del cualquier nivel, entonces partimos de que el primer número cuántico entero es n1, entonces el número máximo que puede tomar el subnivel l para ese nivel es tambié igual l=n1. Es decir que en cualquier nivel de energía habrían un número n1 de subniveles l, el primer subnivel siempre sería s=1 y que corresponde al orbital de la forma so nítida y el ultimo subnivel de ese nivel sería de un valor igual a n1, que corresponde al orbital n1 del respectivo nivel.
La anterior relación número dos (2) nos entrega en cualquier átomo el término n que es una relación de los números cuánticos. Pero hemos hallado la siguiente relación entre el ángulo, n, n1, l, m y Z o número atómico.
![]() (4)
(4)
Donde n es un número total que podría no ser entero y representa a la relación presente entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, l es el segundo número cuántico entero y Z es el número atómico.
![]() (5)
(5)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, l es el segundo número cuántico entero y Z es el número atómico.
![]() (6)
(6)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, l es el segundo número cuántico entero y Z es el número atómico.
![]() (7)
(7)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, l es el segundo número cuántico entero y Z es el número atómico
Aquí a esta anterior relación número 7 para la solución de n, se la hacemos con la aplicación de la formula que resuelve la ecuación de una incognita de segundo grado:
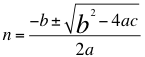 (8)
(8)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, a, b y c son los respectivos coeficientes y términos independientes.
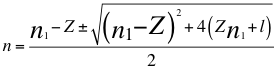 (9)
(9)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, l es el segundo número cuántico entero y Z es el número atómico.
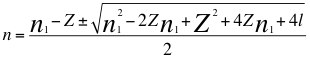 (10)
(10)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, l es el segundo número cuántico entero y Z es el número atómico.
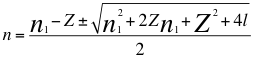 (11)
(11)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, l es el segundo número cuántico entero y Z es el número atómico.
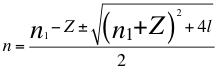 (12)
(12)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, l es el segundo número cuántico entero y Z es el número atómico.
Quiere decir que para el átomo de hidrogeno reemplazamos el valor conseguido de n en la anterior relación número 3 y se consigue con facilidad la constante de Rydberg para el hidrogeno de la siguiente manera:
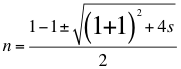 (13)
(13)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, s es el segundo número cuántico entero.
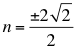 (14)
(14)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón.
![]() (15)
(15)
Donde n es un número total que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón.
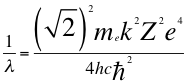 (16)
(16)
Donde λ es la longitud de onda del electrón, mees la masa del electrón, kes la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, nes un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.
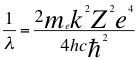 (17)
(17)
Donde λ es la longitud de onda del electrón, mees la masa del electrón, kes la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, nes un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.
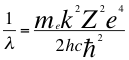 (18)
(18)
Donde λ es la longitud de onda del electrón, mees la masa del electrón, kes la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, nes un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.
La energía de un electrón que orbita cualquier subnivel, de cualquier nivel de energía, en cualquier átomo, lo haríamos con la siguiente relación, obtenida cuando el segundo número cuántico entero l tendría un valor cuántico desde uno (1) hasta el valor que tome el primer número cuántico n1.
![]() (19)
(19)
Donde n es un número total que podría no ser entero y representa la relación total entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, g es el quinto subnivel de energía y Z es el número atómico del átomo.
![]() (20)
(20)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero y Z es el número atómico del átomo.
![]() (21)
(21)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero y Z es el número atómico del átomo.
![]() (22)
(22)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero y Z es el número atómico del átomo.
![]() (23)
(23)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, g es el quinto subnivel de energía y Z es el número atómico del átomo.
![]() (24)
(24)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, g es el quinto subnivel de energía y Z es el número atómico del átomo.
![]() (25)
(25)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, g es el quinto subnivel de energía y Z es el número atómico del átomo.
Nuevamente a esta anterior relación número 25, buscando pues la solución de n, también le aplicamos la ecuación de segundo grado:
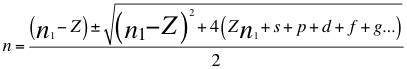 (26)
(26)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, g es el quinto subnivel de energía y Z es el número atómico del átomo.
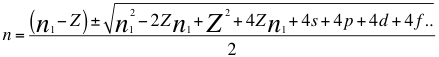 (27)
(27)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, g es el quinto subnivel de energía y Z es el número atómico del átomo.
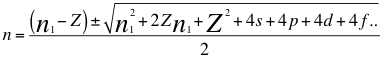 (28)
(28)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, g es el quinto subnivel de energía y Z es el número atómico del átomo.
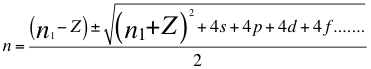 (29)
(29)
Donde n es un número que podría no ser entero y representa la relación entre el ángulo y los números cuánticos enteros del electrón, n1 es el primer número cuántico entero, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, g es el quinto subnivel de energía y Z es el número atómico del átomo.
MOMENTO ANGULAR DEL ELECTRÓN
El momento angular lo vamos a describir en función de los 4 números cuánticos:
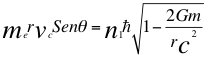 (30)
(30)
Donde me es la masa del electrón, vc es la velocidad cuántica del electrón, r es el radio de la órbita, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n1 es el primer número cuántico entero, ħ es la constante reducida de Planck, G es constante de gravitación universal, m es la masa nuclear atómica y C es la velocidad de la luz en el vacío.
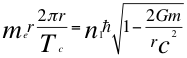 (31)
(31)
Donde me es la masa del electrón, Tc es el período cuántico del electrón, r es el radio de la órbita, n1 es el primer número cuántico entero, ħ es la constante reducida de Planck, G es constante de gravitación universal, m es la masa nuclear atómica y C es la velocidad de la luz en el vacío.
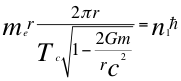 (32)
(32)
Donde me es la masa del electrón, r es el radio de la órbita, Tc es el período cuántico del electrón, n1 es el primer número cuántico entero, ħ es la constante reducida de Planck, G es constante de gravitación universal, m es la masa nuclear atómica y C es la velocidad de la luz en el vacío.
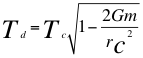 (33)
(33)
Donde Td es el período con tiempo gravitacional, Tc es el período con tiempo cuántico, r es el radio de la órbita, G es constante de gravitación universal, m es la masa nuclear atómica y C es la velocidad de la luz en el vacío.
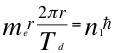 (34)
(34)
Donde me es la masa del electrón, Td es el período con tiempo gravitacional del electrón, r es el radio de la órbita, n1 es el primer número cuántico entero y ħ es la constante reducida de Planck.
![]() (35)
(35)
Donde me es la masa del electrón, v es la velocidad del electrón con tiempo gravitacional, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, n1 es el primer número cuántico entero y ħ es la constante reducida de Planck.
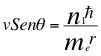 (36)
(36)
Donde v es la velocidad del electrón con tiempo gravitacional, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, me es la masa del electrón, r es el radio de la órbita, n1 es el primer número cuántico entero y ħ es la constante reducida de Planck.
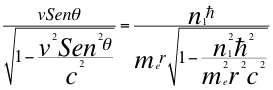 (37)
(37)
Donde v es la velocidad del electrón con tiempo gravitacional, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, me es la masa del electrón, r es el radio de la órbita, n1 es el primer número entero cuántico y ħ es la constante reducida de Planck.
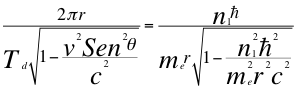 (38)
(38)
Donde Td es el período del electrón con tiempo gravitacional, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, me es la masa del electrón, r es el radio de la órbita, n1 es el primer número entero cuántico y ħ es la constante reducida de Planck.
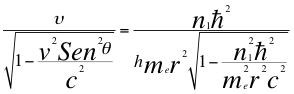 (39)
(39)
Donde h es la constante de Planck, υ es la frecuencia del electrón no dilatada, me es la masa del electrón, r es el radio de la órbita, n1 es el primer número entero cuántico y ħ es la constante reducida de Planck.
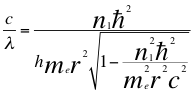 (40)
(40)
Donde λ es la longitud de onda del electrón, h es la constante de Planck, υ es la frecuencia del electrón, me es la masa del electrón, r es el radio de la órbita, n1 es el primer número cuántico entero y ħ es la constante reducida de Planck.
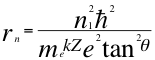 (41)
(41)
Donde r es el radio de la órbita del electrón, n1 es el primer número cuántico entero, ħ es la constante reducida de Planck, me es la masa del electrón, k es la constante de coulomb, Z es el número atómico constante reducida de Planck, e es la carga del electrón y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.
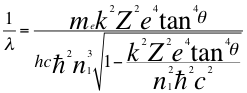 (42)
(42)
Donde λ es la longitud de onda del electrón, h es la constante de Planck, υ es la frecuencia del electrón, me es la masa del electrón, k es la constante de coulomb, Z es el número atómico constante reducida de Planck, e es la carga del electrón, n1 es el primer número cuántico entero y ħ es la constante reducida de Planck.
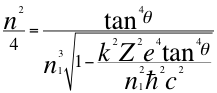 (43)
(43)
Donde n es un número que podía ser no entero y corresponde a la relación total del ángulo con los números cuánticos enteros del electrón, ħ es la constante reducida de Planck, k es la constante de coulomb, Z es el número atómico constante reducida de Planck, e es la carga del electrón, n1 es el primer número cuántico entero y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.
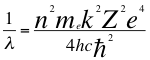 (44)
(44)
Donde λ es la longitud de onda del electrón, n es un número que podía ser no entero y corresponde a la relación total entre el ángulo y los números cuánticos enteros del electrón, me es la masa del electrón, k es la constante de coulomb, Z es el número atómico constante reducida de Planck, e es la carga del electrón, h es la constante de Planck y ħ es la constante reducida de Planck.
3- Conclusiones:
1- La Primera Gran Conclusión de este trabajo es que a este cálculo de la energía del de electrón en subniveles p, d, f, u otros, solo le hace falta en ellos hacer desaparecer la degeneración de los subniveles para que así puedan explicar los experimentos de espectroscopias atómicas, ya que parece que eso solo se consigue agregando a la anterior relación número 25, los efectos que tienen en la formula, la interacción espín-orbita o el llamado también acoplamiento de los momentos angulares de los espines electrónicos individuales, consistente en que los electrones que tienen distintos valores del tercer número cuántico m, tendrían diferentes energías debidas al efecto que sobre ellos ocasionan el momento magnético del núcleo atómico.
2- Cuarta Segunda Gran Conclusión es que Este paso del acoplamiento del momento angular de los espines electrónicos para este trabajo, tiene demasiada importancia y es crucial porque no es un caso simple y primero porque sería la única manera de poder explicar en los experimentos de espectroscopia a todo este esfuerzo, segundo porque la verificación de la energía propuesta en la relación número 51, no sería verificada porque esta resonancia orbital es reflejada en la ley general de conservación del momento angular que inclusive también es válida en objetos celestes.
Los valores energéticos en los distintos niveles de energía vendrían dados a partir de la la anterior relación número 44, donde reemplazamos el valor que tiene n en la anterior relación número 29, para obtener las siguientes relaciones 45, 46, 46, 47, 48, 49, 50 y 51:
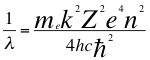 (44)
(44)
Donde λ es la longitud de onda del electrón, n es un número que podía ser no entero y corresponde a la relación total entre el ángulo y los números cuántics enteros del electrón, me es la masa del electrón, k es la constante de coulomb, Z es el número atómico constante reducida de Planck, e es la carga del electrón, h es la constante de Planck y ħ es la constante reducida de Planck.
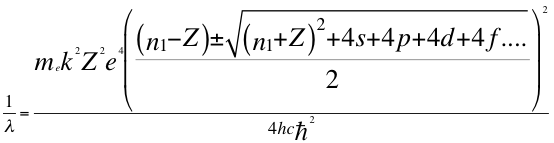 (45)
(45)
Donde λ es la longitud de onda del electrón, h es la constante de Planck, me es la masa del electrón, k es la constante de coulomb, Z es el número atómico, e es la carga del electrón, n1 es el primer número entero cuántico, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, C es la velocidad de la luz en el vacío y ħ es la constante reducida de Planck.
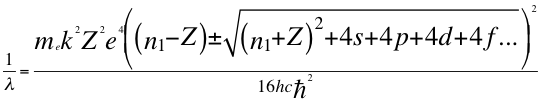 (46)
(46)
Donde λ es la longitud de onda del electrón, h es la constante de Planck, me es la masa del electrón, k es la constante de coulomb, Z es el número atómico, e es la carga del electrón, n1 es el primer número entero cuántico, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, C es la velocidad de la luz en el vacío y ħ es la constante reducida de Planck.
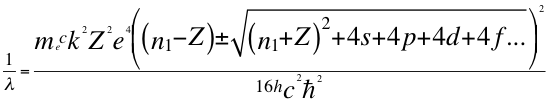 (47)
(47)
Donde λ es la longitud de onda del electrón, me es la masa del electrón, h es la constante de Planck, k es la constante de coulomb, Z es el número atómico, e es la carga del electrón, n1 es el primer número entero cuántico, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía, C es la velocidad de la luz en el vacío y ħ es la constante reducida de Planck.
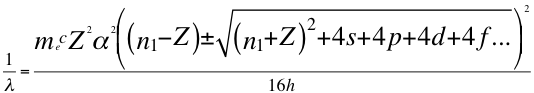 (48)
(48)
Donde λ es la longitud de onda del electrón, me es la masa del electrón, α es la constante de estructura fina, h es la constante de Planck, Z es el número atómico, n1 es el primer número entero cuántico, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía y C es la velocidad de la luz en el vacío.
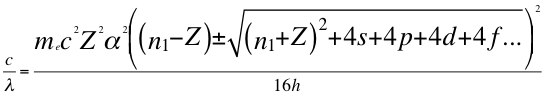 (49)
(49)
Donde λ es la longitud de onda del electrón, me es la masa del electrón, α es la constante de estructura fina, h es la constante de Planck, Z es el número atómico, n1 es el primer número entero cuántico, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía y C es la velocidad de la luz en el vacío.
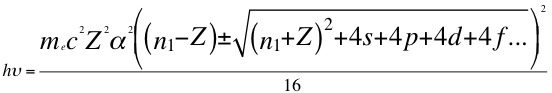 (50)
(50)
Donde h es la constante de Planck, υ es la frecuencia del electrón, me es la masa del electrón, α es la constante de estructura fina, Z es el número atómico, n1 es el primer número entero cuántico, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía y C es la velocidad de la luz en el vacío.
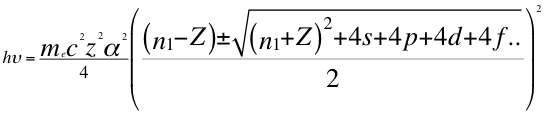 (51)
(51)
Donde h es la constante de Planck, υ es la frecuencia del electrón, me es la masa del electrón, α es la constante de estructura fina, Z es el número atómico, n1 es el primer número entero cuántico, s es el primer subnivel de energía, p es el segundo subnivel de energía, d es el tercer subnivel de energía, f es el cuarto subnivel de energía y C es la velocidad de la luz en el vacío.
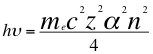 (52)
(52)
Donde h es la constante de Planck, υ es la frecuencia del electrón, me es la masa del electrón, α es la constante de estructura fina, Z es el número atómico, n es un número que dodría ser no entero y corresponde a la representación total de los números cuánticos y C es la velocidad de la luz en el vacío.
3- Una Tercera Gran conclusión sería el hecho de poder recordarles a los lectores el nombre de Dirac y también, que tengan en cuenta la constante de estructura fina que es la siguiente:
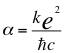 (53)
(53)
Donde α es la constante de estructura fina, k es la constante de coulomb, e es la carga del electrón, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.
4- Una cuarta Gran Conclusión, es el hecho de poder vislumbrar, una posible utilidad de la anterior relación número 51, para invlucrarle el estudio del m o tercer número cuántico.
4- Referencias
[1] Inflación Cuántica textos científicos.
[2] Números cuánticos textoscientíficos.com.
[3] Inflación Cuántica Monografías.
[4] Orbital Atómico
[5] Números Cuánticos.
[6] Átomo de Bohr.
[7] Líneas de Balmer.
[8] Constante Rydberg.
[9] Dilatación gravitacional del tiempo.
[10] Número Cuántico magnético.
[11] Numero Cuántico Azimutal.
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena Colombia. Investigador independiente de problemas biofísicos médicos propios de la memoria, el aprendizaje y otros entre ellos la enfermedad de Alzheimer.
Estos trabajos, que lo más probable es que estén desfasados por la poderosa magia secreta que tiene la ignorancia y la ingenuidad, sin embargo, han sido debidamente presentados también en la “Academia Colombiana de Ciencias Exactas, Físicas y naturales” ACCEFYN.