Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
La masa como frecuencia de una onda gravitacional estudiada con la “ley universal de efecto Doppler” encuentra en este trabajo, una ecuación que satisface tanto a la relatividad general como la especial, relación y estudios que valen la pena de ser contrastados con la teoría de cuerdas. Aquí también se identifican unidades de fuerza a la denominada fuerza ficticia. También aquí se demuestra la curvatura del espacio-tiempo entorno al observador y más si cuenta con masa acelerada.
Palabras claves: Fuerza Ficticia, Fuerza Aparente, Fuerza inercial, Inercia, Tiempo propio, Longitud de onda asociada, Gravedad Cuántica, Doppler Relativista, Dilatación gravitacional del Tiempo.
Abstract
Mass as a gravitational wave studied with the "universal law of Doppler effect" often found in this work, an equation which satisfies both to general relativity as the special relationship and studies that are worth of contrasted with string theory. Here also force the so-called fictitious force units are identified. Also here demonstrates the curvature of space-time environment to the observer and more with accelerated mass.
Key Words: Fictional force, force apparent, inertial force, inertia, own time, length associated waveform, quantum gravity, relativistic Doppler, gravitational time dilation.
1. INTRODUCCIÓN
Como introducción de este artículo queremos recordar las conclusiones del anterior trabajo de la dilatación gravitacional del tiempo en la ley universal del efecto Doppler.
La descripción y el desarrollo de artículo tienen como principio de que si se hace el estudio completo del Doppler, es necesario incluir a la velocidad y trayectoria tanto de la fuente como del observador, que serán descompuestas cada una en dos componentes con respecto al ángulo que describen las trayectorias de cada uno en relación a la recta de vista que los une. Habrán dos vectores que comparten la misma recta de acción y aplicados fijamente en los extremo de dicha recta de visión, estarán situados allí los cosenos de los respectivos ángulos que describen la trayectoria de la fuente y observador vfcosθf y vocosθo con la línea de vista. Vectores que tendrían la misma dirección que podía ser en el mismo sentido o sentido contrario. Por el otro lado estaría el seno del ángulo descrito entre la trayectoria de la fuente y observador vfsenθf y vosenθo que serían siempre paralelas en uno u otro sentido en el mismo plano.
![]() (1)
(1)
![]() (2)
(2)
Donde vf es la velocidad de la fuente, θf es el ángulo descrito entre la línea de visión del observador y la trayectoria de la fuente, vo es la velocidad del observador, θo es el ángulo descrito entre la línea de visión y la trayectoria del observador.
Ahora aplicamos la “Ley universal del efecto Doppler” donde quedan implícitas las velocidades y trayectorias de la fuente y observador: “El cuadrado de la relación entre las frecuencias emitida y observadas más, el cuadrado de la relación entre la velocidad de la fuente y la onda más, el cuadrado de la relación de la velocidad del observador y la onda es igual a la unidad”.
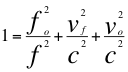 (3)
(3)
Donde fo es la frecuencia emitida por la fuente, f es la frecuencia observada, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació.
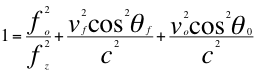 (4)
(4)
Vamos a aplicar la ley universal del efecto Doppler a los cosenos de los respectivos ángulos fuente y observador para encontrar o identificar a fz que es la frecuencia emitida de la fuente corrida hacia el azul:
Donde fo es la frecuencia emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la línea de visión.
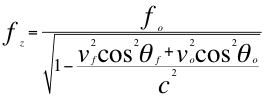 (5)
(5)
Ahora vamos a aplicar la ley universal del efecto Doppler a los senos de los respectivos ángulos y a calcular a la frecuencia final definitiva que seguramente tendría corrimiento hacia el rojo:
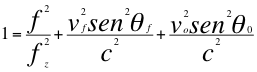 (6)
(6)
Donde f es la frecuencia observada, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
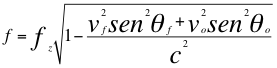 (7)
(7)
Reemplazando a fz de la anterior relación número cinco (5) en la también anterior relación número siete (7) nos queda la siguiente ecuación número ocho (8):
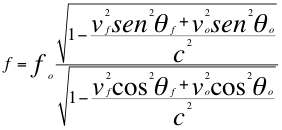 (8)
(8)
![]()
Donde f es la frecuencia observada, fo es la frecuencia emitida por la fuente, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
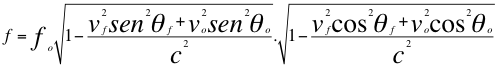 (9)
(9)
![]()
Las anteriores relaciones número ocho (8) y nueve (9) son las ecuaciones que describen el Doppler relativista cuando la fuente y observador se acercan o se alejan incluso con desiguales velocidades angulares.
Para el Doppler relativista en las ondas electromagnéticas es descrita por las anteriores relaciones, pero para el Doppler sonoro bajo la ley universal del efecto Doppler quedaría la descripción de la siguiente manera:
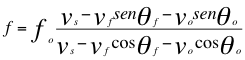 (10)
(10)
Donde f es la frecuencia observada, fo es la frecuencia emitida por la fuente, vs es la velocidad del sonido, vf es la velocidad de la fuente, vo es la velocidad del observador, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
2. DESARROLLO DEL TEMA.
El concepto de masa en la teoría de la relatividad especial tiene dos bifurcaciones: la masa invariante y la masa relativista aparente. La masa relativista aparente es la masa aparente que va a depender del observador y que puede decrecer o incrementarse dependiendo de su velocidad, dirección y sentido, mientras que la masa invariante es independiente del observador e invariante.
Siendo la gravedad una ondulación del espacio-tiempo que se transmite a la velocidad de la luz pues la masa igualmente lo es y entonces, la masa es una distribución continua de materia originada por una cantidad de dilatación gravitacional estacionaria del tiempo en un sitio y cumple la misma “Ley universal del efecto Doppler” es decir, la masa en la ley universal del efecto Doppler tomaría la posición y el sitio de la frecuencia en la relación matemática: “El cuadrado de la relación entre la masa invariante y la masa relativista aparente más, el cuadrado de la relación entre la velocidad de la fuente y la velocidad de la onda de luz mas, el cuadrado de la relación entre la velocidad del observador y la velocidad de la onda de luz es igual a la unidad”:
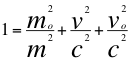 (11)
(11)
Donde mo es la masa invariante que es independiente del observador, m es la masa relativista aparente que depende del observador, v es la velocidad de la fuente, vo es la velocidad del observador y c es la velocidad de la luz.
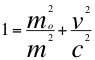 (12)
(12)
Esto implica que la masa tendría unidades de frecuencia en función del tiempo propio percibido por una partícula que ha sido empleado por ejemplo para que la fuerza sea la derivada temporal del momento kg/seg. Desarrollamos entonces la anterior relación considerando que la velocidad de una partícula depende de la trayectoria que tiene dicha partícula con respecto al observador ya que el espacio-tiempo se curva en torno a este:
![]() (13)
(13)
Donde v es la velocidad de la fuente, θ es el ángulo descrito entre la línea de visión del observador y la trayectoria de la partícula.
La relación con respecto al coseno del ángulo θ descrito por la velocidad de una fuente que se acerca al observador que resulta una masa corrida con seguridad hacia el azul, nos queda la relación de la siguiente manera (No se incluye el movimiento del observador para simplificar los cálculos):
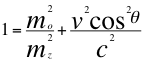 (14)
(14)
Donde mo es la masa invariante de la partícula, mz es la masa invariante pero corrida hacia el azul, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente y la línea de visón del observador y c es la velocidad de la luz.
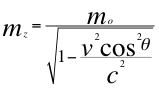 (15)
(15)
Ahora la relación es definida con respecto al seno del ángulo θ descrito por la velocidad de dicha partícula que se aleja del observador tenemos la siguiente relación:
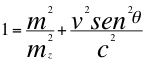 (16)
(16)
Donde m es la masa relativista aparente que depende del observador, mz es la masa invariante de la fuente pero corrida hacia el azul, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente y la línea de visión del observador y c es la velocidad de la luz.
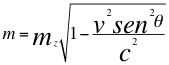 (17)
(17)
Entonces reemplazando a mz en la anterior ecuación nos quedan las siguientes relaciones de la masa relativista aparente m de una fuente cuando se acerca la número diez y ocho (18) y de una fuente que se aleja la número diez y nueve (19) respectivamente del observador:
 (18)
(18)
Donde m es la masa relativista aparente dependiente del observador, mo es la masa invariante de la fuente independiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente con la línea de visión que respectivamente se acerca o se aleja del observador, c es la velocidad de la luz.
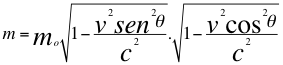 (19)
(19)
Tomando la anterior relación número once (11) como la presentó Einstein que nosotros la vemos apropiada precisamente es para el caso especial cuando el observador es atropellado por la partícula, al estar ubicado precisamente en la misma trayectoria de la fuente, visto esto de la siguiente manera cosθ=1, senθ=0 siendo θ igual a cero (0) grados:
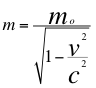 (20)
(20)
Donde mo es la masa invariante independiente del observador, m es la masa relativista aparente dependiente del observador, v es la velocidad de la fuente y c es la velocidad de la luz.
También podemos decir que de la anterior relación número once (11) continuamos igual que Einstein en el desarrollo de las siguientes ecuaciones:
 (11)
(11)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (34)
(34)
Donde m es la masa relativista aparente que depende del observador, mo es la masa invariante independiente del observador, v es la velocidad de la fuente, p es la cantidad de movimiento de la fuente, E es la energía total de la fuente y c es la velocidad de la luz.
![]() (25)
(25)
![]() (26)
(26)
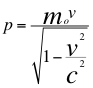 (27) Ó
(27) Ó 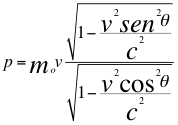 (28)
(28)
Donde m es la masa relativista aparente dependiente del observador, mo es la masa invariante independiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente con la línea de visión que se acerca o se aleja del observador y c es la velocidad de la luz.
Si reemplazamos en esta anterior relación número veinte y cuatro (24), el valor de la masa relativista aparente m que tiene en la también anterior relación número veinte y ocho (28) nos queda de la siguiente manera toda la relación en función únicamente de mo de la masa invariante para una fuente que se acerca al observador:
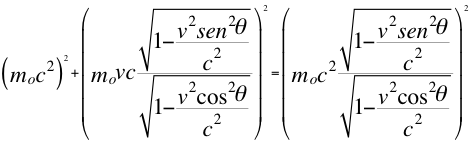 (30)
(30)
Donde m es la masa relativista aparente dependiente del observador, mo es la masa invariante independiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente con la línea de visión que se acerca del observador y c es la velocidad de la luz.
Veamos esta misma ecuación expresada para la cantidad de movimiento como queda de la siguiente manera para una fuente que se acerca al observador:
![]() (21)
(21)
![]() (22)
(22)
 (30)
(30)
Donde m es la masa relativista aparente dependiente del observador, mo es la masa invariante independiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente con la línea de visión que se acerca al observador y c es la velocidad de la luz.
Se puede decir que realmente nos vamos a referir solo a la masa como Doppler y como partícula cuando el observador se encuentra y choca con la fuente porque especialmente está ubicado en la misma trayectoria original de la fuente θ=0 que es la siguiente relación:
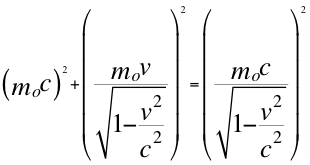
Donde m es la masa relativista aparente que depende del observador, mo es la masa invariante independiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente con la línea de visión que se acerca al observador y c es la velocidad de la luz.
![]() (22)
(22)
LA MASA COMO ONDA GRAVITACIONAL
La “Ley universal del efecto Doppler” con respecto al movimiento acelerado dice: “el cuadrado de la relación entre la frecuencia emitida y observada más, la relación entre el producto de la aceleración de la fuente por el radio y el cuadrado de la velocidad de la onda de luz más, la relación entre el producto de la aceleración del observador por el radio y el cuadrado de la velocidad de la onda de luz es igual a la unidad”:
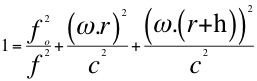 (32)
(32)
Donde fo es la frecuencia emitida, f es la frecuencia observada, ω es la velocidad angular, r es el radio de rotación de la velocidad angular, h es la distancia entre el observador y la fuente y c es la velocidad de la luz. 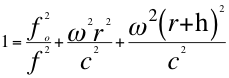 (32)
(32)
Reemplazando en la anterior relación a la masa por la frecuencia y a la velocidad angular por la aceleración gravitacional equivalente encontramos la siguiente relación:
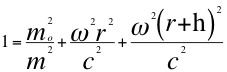 (33)
(33)
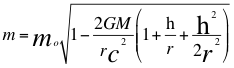 (34)
(34)
Donde m es la masa relativista aparente de la fuente dependiente del observador, mo es la masa invariante de la fuente independiente del observador, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico generador del campo gravitatorio, r es el radio del planeta, c es la velocidad de la luz y h es la altura del observador.
![]() (35)
(35)
LONGITUD DE ONDA ASOCIADA A LA MASA DE LOS CUERPOS.
La longitud de onda que un físico francés asoció a la materia realmente no está efectivamente asociada a la íntima materia como tal, solo está asociada precisamente es a las ondas electromagnéticas que originan las partículas mediante la siguiente fórmula:
![]() (36)
(36)
Donde λ es la longitud de onda asociada a la partícula de masa aparente m que se mueve a la velocidad v y h es la constante Planck.
Viendo la formula se aprecia fácilmente, que a medida que la masa del cuerpo o su velocidad aumenta, disminuye considerablemente la longitud de onda asociada específicamente a esa cantidad de movimiento. Si bien puede ser cierto que la hipótesis se puede aplicar a la cantidad de movimiento de toda la materia incluso los cuerpos macroscópicos, que también tendrían asociada una longitud de onda a su oportuna cantidad de movimiento aunque resulte tan pequeña que en ellos sea imposible apreciar las características ondulatorias pero es del movimiento. En el interferómetro de neutrones, se pudo ya apreciar que estos no actúan tan claramente solo como ondas mecano cuánticas sino que también dichas ondas se encontraban directamente sujetas a la fuerza de la gravedad donde si está implicada la longitud de onda asociada a la masa invariante y aparente de los cuerpos.
En la ley universal del efecto Doppler se encuentra que realmente la masa de los cuerpos es una cantidad de dilatación gravitacional del tiempo estacionaria de la ondulación gravitacional del espacio-tiempo que contiene una densidad y determinada presión de la materia, que tiene también asociada una longitud de onda aquí si con toda propiedad se puede afirmar que está verdaderamente asociada a la materia y a la naturaleza intima de la masa invariante de los cuerpos.
![]() (36)
(36)
Donde λ en m/kg es la longitud de onda en metros por kilo asociada a la masa m en kg/sg de la fuente y c es la velocidad de la luz en el vacío.
![]() (37)
(37) ![]() (37)
(37)
Donde λ en m/kg es la longitud de onda en metros por kilo asociada a la masa m en kg/sg de la fuente y c es la velocidad de la luz en el vacío.
Se puede apreciar que la longitud de onda asociada a la masa invariante de un cuerpo en metros/kg como materia, es totalmente independiente de que tenga al instante una eventual cantidad de movimiento que necesite una constante de Planck para asociar una longitud de onda de De-Broglie de acuerdo a la velocidad, dirección y sentido.
Sabemos que la relación, sin tener en cuenta el movimiento relativo del observador, entre la masa relativista aparente y la masa invariante depende de si la fuente se acerca o se aleja del observador, tal como lo describen las anteriores ecuaciones número diez y ocho (18) y diez y nueve (19) que sin embargo seguidamente las vamos a recordar:
 (18)
(18)
Donde m es la masa relativista aparente dependiente del observador, mo es la masa invariante de la fuente independiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente con la línea de visión que respectivamente se acerca o se aleja del observador, c es la velocidad de la luz.
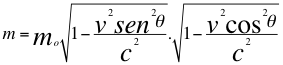 (19)
(19)
Donde m es la masa relativista aparente dependiente del observador, mo es la masa invariante de la fuente independiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente con la línea de visión que respectivamente se acerca o se aleja del observador, c es la velocidad de la luz.
Entonces reemplazando la anterior relación número treinta y siete (37) en las relaciones número diez y ocho (18) y diez y nueve (19) nos resulta la relación entre la longitud de onda gravitacional asociada a la masa invariante y aparente:
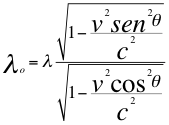 (38)
(38)
Donde λo es la longitud de onda gravitacional asociada a la masa invariante de la fuente independiente del observador, λ es la longitud de onda gravitacional asociada a la masa aparente dependiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente y la línea de visión que respectivamente se acerca o se aleja del observador, c es la velocidad de la luz.
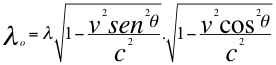 (39)
(39)
Donde λo es la longitud de onda gravitacional asociada a la masa invariante de la fuente independiente del observador, λ es la longitud de onda gravitacional asociada a la masa aparente dependiente del observador, v es la velocidad de la fuente, θ es el ángulo descrito entre la trayectoria de la fuente y la línea de visión que respectivamente se acerca o se aleja del observador, c es la velocidad de la luz.
RELATIVIDAD GENERAL Y ESPECIAL UNIFICADAS
Tomando las anteriores relaciones número treinta y cuatro (34) de la relatividad general, con las también anteriores relaciones número diez y ocho (18) y número diez y nueve (19) de la relatividad especial. Asociando estas relaciones encontramos una relación general que abarca ambas teorías alrededor de un observador acelerado de masa M:
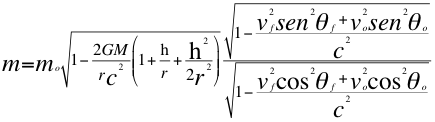 (40)
(40)
Donde m es la masa aparente de la fuente observada, mo es la masa invariante de la fuente o cuerpo observado, vf es la velocidad de la fuente observada, vo es la velocidad del observador acelerado, θf es el ángulo descrito entre la trayectoria de la fuente con la línea de visión que respectivamente se acerca o se aleja del observador, θo es el ángulo descrito entre la trayectoria del observador y la línea de visión que respectivamente se acerca o se aleja de la fuente, c es la velocidad de la luz, M es la masa del observador acelerado, G es la constante de gravitación universal, r es el radio del observador acelerado y h es la altura de la fuente observada.. 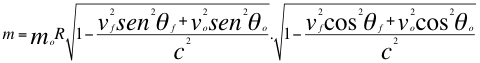 (41)
(41)
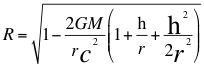 (42)
(42)
La anterior ecuación número cuarenta (40) corresponde a la descripción de una partícula o cuerpo que se acerca a un observador acelerado de masa M y, la relación número cuarenta y uno (41) corresponde es cuando esa misma partícula descrita se aleja del respectivo observador acelerado.
3. CONCLUSIONES.
a)- La gran conclusión de este trabajo es la ecuación que integra tanto a la relatividad general como la relatividad especial.
b)- Otra gran conclusión de este trabajo es el de haberle conseguido unidades de fuerza, a la cantidad de movimiento identificada como fuerza ficticia, aparente o inercial.
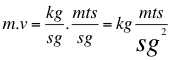 (43)
(43)
c)- El espacio-tiempo se curva entorno al observador mucho más con masa acelerada.
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[01] Relatividad General
[02] Relatividad General
[03] corrimiento al rojo gravitacional
[04] efecto Doppler relativista
[05] corrimiento al rojo
[06] corrimiento al rojo gravitacional
[07] efecto doppler relativista
[08] efecto doppler relativista
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.