The Orbital Velocity of the Electron
Por Heber Gabriel Pico Jiménez MD
Resumen
La velocidad orbital del electrón en el átomo a la velocidad de la luz, demuestra que el espacio-tiempo de la relatividad especial en realidad, sea curvo. La evolución temporal suave del electrón, que es la evolución responsable de las predicciones en la mecánica cuántica, en esa evolución la velocidad orbital para un observador interno es igual a la velocidad de la luz mientras que en la evolución temporal abrupta del electrón, para otro tipo de observador que es el que establece una medida, la velocidad orbital es la que le corresponde al observador en el planeta. De verdad sí constituye un error pensar que la medida puede hacerla un observador ubicado dentro del sistema cuántico cuando en realidad, el observador real que establece la medida tiene unas condiciones experimentales diferentes y la velocidad orbital del observador es totalmente distinta.
Palabras claves: Gravedad Cuántica, Colapso de la función de onda Cuántica, Velocidad Orbital.
Abstract
The orbital velocity of the electron in the atom to the speed of light, shows that the space-time of special relativity is indeed curved. The soft temporal evolution of electron, which is responsible for the accuracy of the predictions evolution give it mechanical quantum, the orbital velocity for an internal observer is equal to the speed of light while, in the abrupt temporal evolution of electron for another observer who is establishing a measurement, the orbital velocity is you on the planet. Really Yes constitutes a mistake thinking that measure can make it an observer located inside the quantum system, when in fact the real observer laying down the measure, has experimental conditions and different orbital velocity.
Keywords: Gravity quantum, quantum, speed Orbital wave function collapse.
1. Introducción
Este artículo se basa sobre todo en la última publicación denominada Gravedad Cuántica, Dilatación unificada del tiempo y el Espacio-tiempo curvo de la gravedad cuántica.
2. Desarrollo del Tema.
El espacio-tiempo de este trabajo, involucra a la velocidad orbital del observador, velocidad orbital que choca con la velocidad lineal del objeto en el estudio del movimiento de las partículas.
El espacio-tiempo unificado que involucra a la velocidad orbital del observador, tal como una evolución temporal no lineal en la siguiente relación:
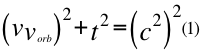
Donde t es el tiempo, v es la velocidad relativa de la partícula, vorb es la velocidad orbital del observador de la partícula y c la velocidad de la luz en el vacío.
ESPACIO TIEMPO CURVO DEL ÁTOMO
En la relatividad especial y la mecánica cuántica, la velocidad orbital del observador que estudia al electrón en el átomo es igual a la velocidad de la luz:
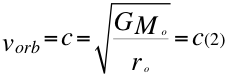
Donde vorb es la velocidad orbital del observador suave de la partícula con respecto al tiempo suave de la mecánica cuántica, G es la constante gravitacional, Mo es la masa nuclear que crea el campo gravitatorio del núcleo atómico, ro es el radio nuclear del átomo y c la velocidad de la luz en el vacío.
A medida que se incrementa la masa gravitacional, se incrementa el radio másico y la velocidad orbital se mantiene constante igual a la velocidad de la luz.
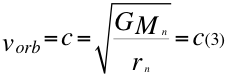
Donde vorb es la velocidad orbital del observador suave de la partícula con respecto al tiempo suave de la mecánica cuántica, G es la constante gravitacional, Mn es la masa nuclear que crea el campo gravitatorio del electrón, rn es el radio gravitacional del observador suave y c la velocidad de la luz en el vacío.
![]()
Donde M1 es la nueva masa gravitacional atómica útil para el par siguiente de electrones, M0 es la masa nuclear gravitacional atómica, m es la masa del electrón.
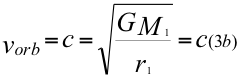
Donde vorb es la velocidad orbital del observador suave de la partícula con respecto al tiempo suave de la mecánica cuántica, G es la constante gravitacional, M1 es la nueva masa nuclear que crea el campo gravitatorio del electrón, r1 es el nuevo radio gravitacional del observador suave y c la velocidad de la luz en el vacío.
Si reemplazamos a 2 y 3 en la ecuación número uno (1), nos queda la siguiente relación:
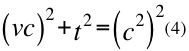
Donde t es el tiempo, v es la velocidad relativa de la partícula y c la velocidad de la luz en el vacío.
Despejamos al tiempo:
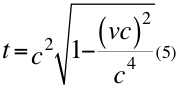
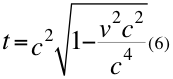
Donde t es el tiempo, v es la velocidad relativa de la partícula y c la velocidad de la luz en el vacío.
Remplazando el tiempo en la anterior relación número 4 y tenemos la siguiente ecuación:
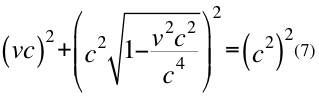
Donde v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
Ahora multiplicamos a la anterior relación por la masa invariante de la partícula:
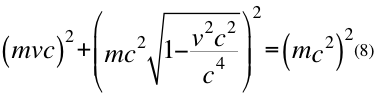
Donde m es la masa invariante de la partícula, v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
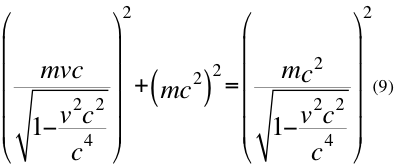
Donde m es la masa invariante de la partícula, v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
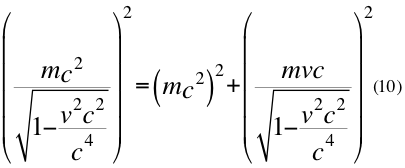
Donde m es la masa invariante de la partícula, v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
En la energía cinética multiplicamos e inmediatamente dividimos por el cuadrado de la velocidad de la luz en el vacío.
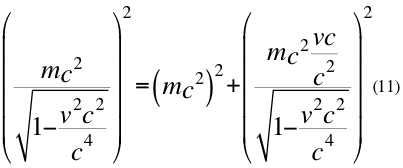
Donde m es la masa invariante de la partícula, v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
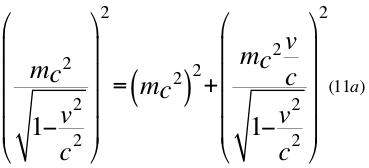
Donde m es la masa invariante de la partícula, v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
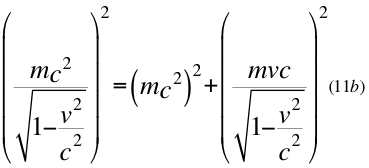
Donde m es la masa invariante de la partícula, v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
Esta anterior relación podíamos describirla de la siguiente manera:
![]()
Donde Et es el de energía total de la partícula en movimiento, Er es el vector de energía en reposo de dicha partícula y Ec es el vector de la energía cinética de la misma partícula.
ENERGÍA CINÉTICA DE UNA PARTÍCULA QUE SE MUEVE EN UN CAMPO GRAVITACIONAL
La energía cinética de una partícula en movimiento y en un espacio-tiempo curvado por el observador es la siguiente:
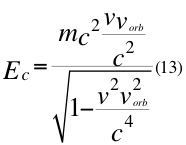
Donde Ec es la energía cinética de la partícula en movimiento, m es la masa invariante de la partícula, vorb es la velocidad orbital del observador de la partícula, v es la velocidad relativa de la partícula y c la velocidad de la luz en el vacío.
ENERGÍA EN REPOSO DE UNA PARTÍCULA QUE SE MUEVE EN UN CAMPO GRAVITACIONAL
El vector de la energía en reposo siempre viaja con la partícula. La energía en reposo de una partícula es la cantidad de energía invariante que hay en la cantidad de masa invariante de la partícula que se encuentra en movimiento es la siguiente:
![]()
Donde Er es la energía en reposo de la partícula en movimiento, m es la masa invariante de la partícula y c la velocidad de la luz en el vacío.
La ENERGÍA TOTAL DE UNA PARTÍCULA QUE SE MUEVE EN UN CAMPO GRAVITACIONAL
La energía total de una partícula que está en movimiento y en un espacio-tiempo curvado por el observador es la siguiente:
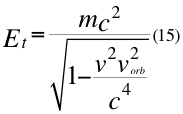
Donde Et es la energía total de la partícula en movimiento, m es la masa invariante de la partícula, v es la velocidad relativa de la partícula que se mueve, vorb es la velocidad orbital del observador de la partícula y c la velocidad de la luz en el vacío.
ÁNGULO θ TETHA
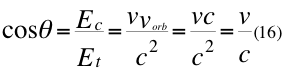
Donde Ec es la energía cinética de la partícula en movimiento, Et es la energía total de la partícula,v es la velocidad relativa de la partícula y c la velocidad de la luz.
ESPACIO TIEMPO CURVO DEL FOTÓN
El espacio tiempo en que se mueve el fotón también es curvo y el observador tiene nuestra velocidad orbital:
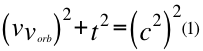
Donde t es el tiempo, v es la velocidad relativa de la partícula, vorb es la velocidad orbital del observador de la partícula y c la velocidad de la luz en el vacío.
Pero en el fotón la velocidad orbital es la de nosotros como observadores aunque la velocidad de la partícula, es igual a la velocidad de la luz y la anterior ecuación del espacio-tiempo se convierte en la siguiente:
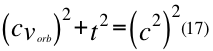
Donde t es el tiempo, vorb es la velocidad orbital del observador de la partícula y c la velocidad de la luz en el vacío.
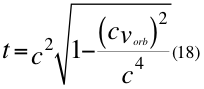
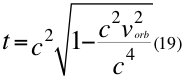
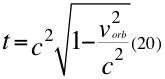
Donde t es el tiempo, vorb es la velocidad orbital del observador de la partícula y c la velocidad de la luz en el vacío.
Remplazando el tiempo tenemos:
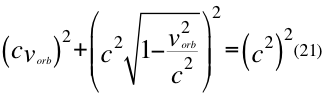
Donde vorb es la velocidad orbital del observador de la partícula y c es la velocidad de la luz en el vacío.
Ahora multiplicamos a la anterior relación por la masa invariante de la partícula:
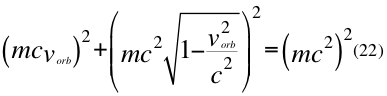
Donde m es la masa invariante de la partícula, vorb es la velocidad orbital del observador de la partícula y c es la velocidad de la luz en el vacío.
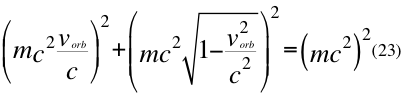
Donde m es la masa invariante de la partícula, vorb es la velocidad orbital del observador de la partícula y c es la velocidad de la luz en el vacío.
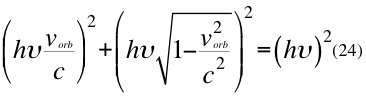
Donde h es la constante de Planck,υ es la frecuencia del fotón, vorb es la velocidad orbital del observador de la partícula y c es la velocidad de la luz en el vacío.
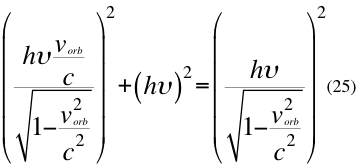
Donde h es la constante de Planck,υ es la frecuencia del fotón, vorb es la velocidad orbital del observador de la partícula y c es la velocidad de la luz en el vacío.
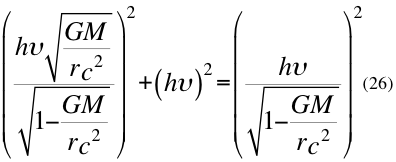
Donde h es la constante de Planck,υ es la frecuencia del fotón, vorb es la velocidad orbital del observador de la partícula, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, r es el radio gravitacional del observador y c es la velocidad de la luz en el vacío.
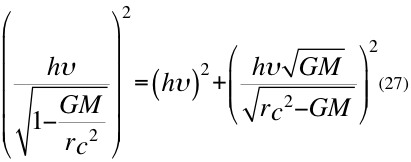
Donde h es la constante de Planck,υ es la frecuencia del fotón, vorb es la velocidad orbital del observador de la partícula, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, r es el radio gravitacional del observador y c es la velocidad de la luz en el vacío.
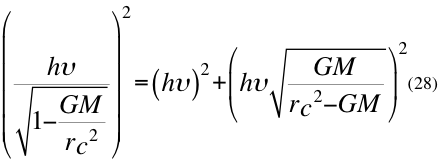
Donde h es la constante de Planck,υ es la frecuencia del fotón, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, r es el radio gravitacional del observador y c es la velocidad de la luz en el vacío.
3- Conclusiones:
a) LA PRIMERA GRAN CONCLUSIÓN de este trabajo es la longitud de onda total del espacio-tiempo donde se encuentra involucrada velocidad orbital del observador:
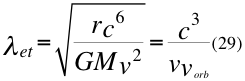
Donde λet es la longitud de onda del espacio-tiempo, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, v es la velocidad relativa de la partícula, vorb es la velocidad orbital del observador de la partícula, r es el radio gravitacional del observador y c la velocidad de la luz en el vacío.
b) LA SEGUNDA GRAN CONCLUSIÓN de este trabajo es la frecuencia de la Onda total del espacio-tiempo donde se encuentra involucrada la velocidad orbital del observador:
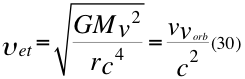
Donde υet es la frecuencia de la onda espacio temporal, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, r es el radio gravitacional del observador, vorb es la velocidad orbital del observador de la partícula, v es la velocidad relativa de la partícula y c la velocidad de la luz en el vacío.
c) UNA TERCERA GRAN CONCLUSIÓN de este trabajo es que el producto de la longitud de onda por la frecuencia de la misma onda espacio temporal.
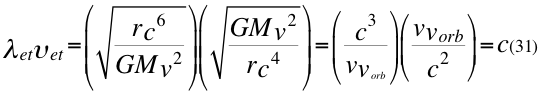
Donde λg es la longitud de onda gravitacional, υ es la frecuencia de la onda gravitacional, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, r es el radio gravitacional del observador, v es la velocidad relativa de la partícula, vorb es la velocidad orbital del observador de la partícula, v es la velocidad relativa de la partícula y c la velocidad de la luz en el vacío.
d) UNA CUARTA GRAN CONCLUSIÓN de este trabajo es la ecuación del movimiento del fotón como partícula en la misma relación donde se encuentra involucrada la velocidad orbital del observador.
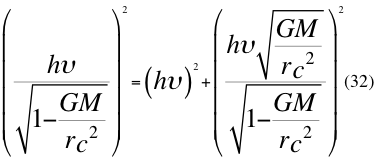
Donde h es la constante de Planck,υ es la frecuencia del fotón, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, r es el radio del campo gravitatorio donde se encuentra el observador y c es la velocidad de la luz.
e) UNA QUINTA GRAN CONCLUSIÓN de este trabajo es la energía cinética de una partícula tiene involucrada a la velocidad orbital del observador en la misma relación.
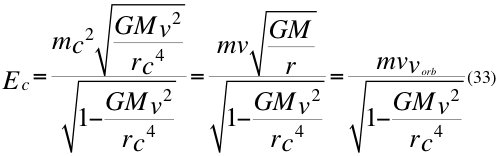
Donde Ec es la energía cinética de la partícula en movimiento, m es la masa invariante de la partícula, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, r es el radio del campo gravitatorio donde se encuentra el observador, v es la velocidad relativa de la partícula, vorb es la velocidad orbital del observador de la partícula y c la velocidad de la luz en el vacío.
e) UNA SEXTA GRAN CONCLUSIÓN de este trabajo es que la relatividad general es el observador de la mecánica cuántica. La relatividad general curva al espacio-tiempo plano de la mecánica cuántica. El tiempo de la relatividad general, es la evolución temporal abrupta no colapsada de la mecánica cuántica.
e) UNA SEPTIMA GRAN CONCLUSIÓN de este trabajo es el PROBLEMA de la MEDIDA de la mecánica cuántica. Esta conclusión trata de resumir la solución del problema de la medida, comparando a la energía cinética de un electrón, medida hipotéticamente por un observador intrínseco quien efectúa las predicciones dela mecánica cuántica ubicado en el estado propio puro, compara esa cifra con la medida de la misma partícula que hace otro observador externo quien se encuentra ubicado en cualquier laboratorio experimental de la superficie del planeta Tierra.
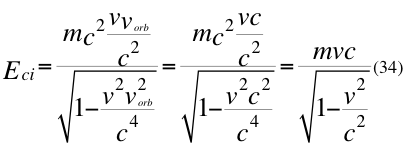
Donde Eci es la energía cinética de la partícula en movimiento medida por un observador intrínseco, m es la masa invariante de la partícula, vorb es la velocidad orbital del observador de la partícula, v es la velocidad relativa de la partícula y c la velocidad de la luz en el vacío.
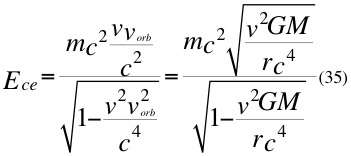
Donde Ece es la energía cinética de la partícula en movimiento medida por un observador externo, m es la masa invariante de la partícula, G es la constante gravitacional, M es la masa que crea el campo gravitatorio, r es el radio del campo gravitatorio donde se encuentra el observador, v es la velocidad relativa de la partícula y c la velocidad de la luz en el vacío.
4- Referencias
REFERENCIAS DEL ARTÍCULO.
[15] Espacio tiempo curvo de la gravedad cuántica
[14] Dilatación unificada del tiempo
[13] Gravedad Cuántica
[12] Efecto Doppler Relativista.
[11] Energía en Reposo
[10] Onda Gravitacional
[09] Ondas de materia
[08] Ondas gravitacionales de vacío cuántico.
[07] Ondas gravitacionales de vacío cuántico.
[06] Tercer número cuántico
[05] Electron como cuasipartícula
[04] Hibridación del Carbono
[03] tercer número cuántico
[02] Hibridación del carbono.
[01] Electrón Cuasipartícula.
[1] Nueva tabla periódica.
[2] Nueva tabla periódica.
[3] Ciclo del Ozono
[4] Ciclo del Ozono
[5] Barrera Interna de Potencial
[6] Barrera Interna de Potencial
[7] Ácido Fluoroantimónico.
[8] Ácido Fluoroantimónico.
[9] Dióxido de cloro
[10]Dióxido de cloro
[11]Pentafluoruro de Antimonio
[12]Pentafluoruro de Antimonio
[13]Tetróxido de Osmio
[14]Enlaces Hipervalentes
[15]Enlaces en moléculas Hipervalentes
[16]Nueva regla del octeto
[17]Estado fundamental del átomo
[18]Estado fundamental del átomo
[19]Barrera rotacional del etano.
[20]Enlaces de uno y tres electrones.
[21]Enlaces de uno y tres electrones.
[22]Origen de la barrera rotacional del etano
[23]Monóxido de Carbono
[24]Nueva regla fisicoquímica del octeto
[25]Células fotoeléctricas Monografías.
[26]Células Fotoeléctricas textoscientificos.
[27]Semiconductores Monografías.
[28]Semiconductores textoscientificos.
[29]Superconductividad.
[30]Superconductividad.
[31]Alotropía.
[32]Alotropía del Carbono.
[33]Alotropía del Oxígeno.
[34]Ozono.
[35]Diborano
[36]Semiconductores y temperatura.
REFERENCIAS DE LA TEORÍA
[1] Número cuántico magnético.
[2] Ángulo cuántico
[3] Paul Dirac y Nosotros
[4] Numero cuántico Azimutal monografías
[5] Numero cuántico Azimutal textoscientificos
[6] Inflación Cuántica textos científicos.
[7] Números cuánticos textoscientíficos.com.
[8] Inflación Cuántica Monografías
[9] Orbital Atómico
[10] Números Cuánticos.
[11] Átomo de Bohr.
[12] Líneas de Balmer.
[13] Constante Rydberg.
[14] Dilatación gravitacional del tiempo.
[15] Número Cuántico magnético.
[16] Numero Cuántico Azimutal.
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena Rep. de Colombia. Investigador independiente de problemas biofísicos médicos propios de la memoria, el aprendizaje y otros entre ellos la enfermedad de Alzheimer.
Estos trabajos, que lo más probable es que estén desfasados por la poderosa magia secreta que tiene la ignorancia y la ingenuidad, sin embargo, como cualquier representante de la comunidad académica que soy, también han sido debidamente presentados sobretodo este se presentó en Mayo 24 del 2015 en la “Academia Colombiana de Ciencias Exactas, Físicas y Naturales” ACCEFYN.