Cálculo de las cantidades de energía intercambiadas en cada proceso

Proceso Politrópico

Calor Intercambiado:

Por el primer principio y la ecuación (22), para un mol de gas ideal

δQ = C.dT = C_V.dT + P.dV  entre dos estados 1 y 2:

(pues C = cte)

Variación de Energía Interna

De la ecuación (6): dU = C_V .dT, entre dos estados 1 y 2:

(suponiendo que C_V = cte)

Variación de la entalpía

De la ecuación (13): dH = C_P.dT

(suponiendo que C_P = cte)

Trabajo exterior

Cuando se conocen las capacidades caloríficas molares C y C_V, se puede calcular W aplicando el Primer Principio:

Q = ΔU + W por lo tanto W = Q - ΔU reemplazando:

W = C (T₂ - T₁) - C_V(T₂ - T₁) = (C - C_V) (T₂ - T₁)     (29)

Si se conoce el exponente politrópico n , partimos de la ecuación:

Reemplazando:

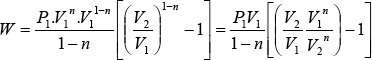
Reemplazando K y sacando factor común V₁^1-n

Como P₁.V₁ⁿ = P₂.V₂ⁿ

por lo tanto

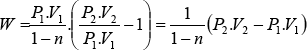 (30)

O también , como P₁.V₁ =R.T₁  y  P₂.V₂ = R.T₂

  (31)

Trabajo de circulación

Conociendo C y Cp se puede calcular Wc aplicando la ecuación del primer principio:

Q = ΔH + Wc

por lo tanto

Wc = Q - ΔH

reemplazando:

Wc = C(T₂ - T₁) - Cp (T₂ - T₁) = (C - Cp)(T₂ - T₁)    (32)

Conociendo el exponente politrópico partimos de la ecuación:

De donde

Reemplazando:

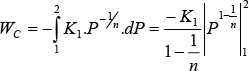
multiplicando por (-1) numerador y denominador y reemplazando K₁:

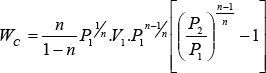
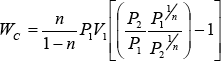
como:

   (33)

O también:

   (34)

Relación entre el trabajo exterior y el trabajo de circulación

Si comparamos las ecuaciones (31) y (34), deducimos que entre dos estados de una transformación politrópica, se cumplirá:

Wc = n.W (35)

o sea que el trabajo de circulación es igual al trabajo exterior multiplicado por el exponente politrópico. En una transformación isotérmica donde n = 1, ambos trabajos son iguales.

Proceso Adiabático

En un proceso adiabático : Q =0 , C=0 , La ecuación de una adiabática será: (reemplazando n por γ en las

ecuaciones (26) , (27) y (28):

Tomando como parámetros P y V:

V.P^γ = cte

Tomando T y V :

V.T^γ−1 = cte

Tomando T y P:

Calor intercambiado

Como ya dijimos: δQ = 0 en consecuencia Q = 0, entre los estados 1 y 2.

Variación de energía interna

Variación de entalpía

Trabajo exterior

En la ecuación (29), como C = 0 , se cumple que:

W = C_V(T₂ - T₁) = C_V(T₁ - T₂)

Expresión que podría obtenerse del primer principio:

W = Q - ΔU = -ΔU = C_V(T₂ - T₁) = C_V(T₁ - T₂)

Esta ecuación nos dice que en una expansión adiabática, donde W es positivo, la diferencia T1 – T2 debe ser positiva, es decir T2>T1. Esto indica de que en la expansión adiabática el gas sufre un enfriamiento.

También se puede obtener una expresión del trabajo exterior, a partir de las ecuaciones (30) y (31), reemplazando n por γ.

Trabajo de circulación

Reemplazando C=0 en la ecuación (32)

W_C = - C_P(T₂ - T₁) = C_P(T₁ - T₂)

O también por la expresión del primer principio:

W_C = Q - ΔH = -ΔH = C_P(T₂ - T₁) = C_P(T₁ - T₂)

Obtenemos otras ecuaciones reemplazando n por γ en (33) y (34):

ó

Relación entre W_e y W_C

Reemplazando n por γ en la ecuación (35) se cumple:

W_C = γ.W_e

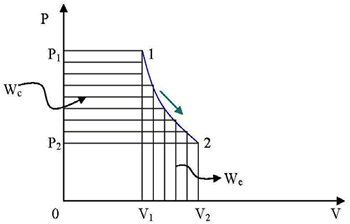
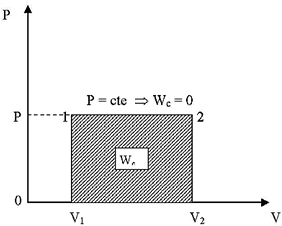
Proceso Isobárico

En un proceso isobárico P=cte , C = C_P y n = 0

Calor intercambiado

Aplicando la ecuación (22) para un mol de gas:

δQ = C.dT = C_P.dT Para dos estados 1 y 2:

También se puede calcular aplicando la expresión del primer principio:

Q = ΔU + W

Variación de la energía interna

Variación de entalpía

Se puede observar que Q = ΔH

Trabajo exterior

Aplicando la ecuación (29) y como C = C_P, resulta:

W = (C_P - C_V)(T₂ - T₁) y por la ecución de Mayer:

W = R.(T₂ - T₁)

También se puede calcular aplicando la ecuación:

Como P es constante: W = P(V₂ - V₁)

Trabajo de circulación

Reemplazando C =CP en la ecuación (32) resulta

W = (C_P - C_P)(T₂ - T₁) = 0

Este mismo resultado se obtiene aplicando la ecuación:

como P = cte entonces dP=0 luego: W_C=0

O también de las ecuaciones (33) y (34) pues n=0.

Proceso Isocórico

En un proceso isocórico V=cte , C = C_V y n = ∞

Calor Intercambiado

Aplicando la ecuación (22) para un mol de gas:

δQ = C.dT = C_V.dT

Para dos estados 1 y 2:

Variación de energía interna

Se puede observar que en esta transformación Q=ΔU

Variación de entalpía

Trabajo exterior

Aplicando la ecuación (29) y como C = CV, resulta:

W = (C_V - C_V)(T₂ - T₁) = 0

También se puede calcular aplicando la ecuación:

como V=cte entonces dV=0 luego W=0

También se verifica que W es nulo si reemplazamos n=∞ en las ecuaciones (30) y (31).

Trabajo de circulación

Reemplazando C =CV en la ecuación (32) resulta

W = (C_V - C_P)(T₂ - T₁) = (C_P - C_V)(T₁ - T₂) = R(T₁ - T₂)

Este mismo resultado se obtiene aplicando la ecuación:

∫−=21.dPVWC como V = cte

W_C = - V(P₂ - P₁)= V(P₁ - P₂)

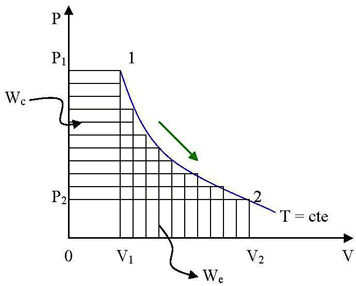
Proceso Isotérmico

En un proceso isotérmico T=cte, C=∞ n=1

Calor intercambiado

Para calcular Q no podemos aplicar la ecuación (22) pues llegaríamos a una indeterminación, ya que C=∞ y dT=0.

Recurrimos entonces a la expresión del primer principio:

Q = ΔU + W como veremos que ΔU=0, directamente Q=W

Variación de energía interna

  como dT =0 entonces ΔU=0

Variación de entalpía

   como dT=0 entonces ΔH=0

Trabajo exterior

Para calcular W no podemos utilizar la ecuación (29) pues llegamos a una indeterminación. Debemos aplicar entonces la ecuación:

Como para un mol de gas ideal P.V=R.T entonces reemplazando

como también se cumple la ecuación P.V =cte ya que en la (26) se puede reemplazar n=1, será:

P₁V₁ = P₂V₂  luego y también:  

Trabajo de circulación

Por la misma razón explicada anteriormente, el trabajo de circulación se deberá calcular mediante la ecuación:

reemplazando:

Se puede observar que WC = W, lo cual cumple la ecuación (35).