Experimento de Joule

Energía interna y entalpía de un gas ideal

En el año 1844, Joule efectuó experiencias con los gases dejándolos expandir en el vacío.

El experimento consistió en colocar dos recipientes A y B, que pueden comunicarse entre sí operando el robinete R, sumergidos en un calorímetro de agua, cuya temperatura puede medirse con el termómetro t.

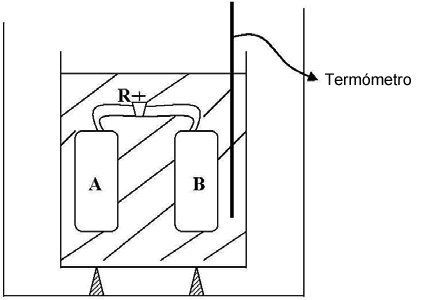
Se inicia el experimento colocando una masa de gas en A y haciendo el vacío en B. Todo el conjunto tendrá la temperatura del agua del calorímetro. Abriendo el robinete R, el gas encerrado en A se expande hasta ocupar el volumen de los recipientes A y B. Midiendo la temperatura del agua del calorímetro, se puede constatar que la temperatura no ha variado. Esto indica que el calor intercambiado entre el gas y el agua es cero Q = 0. Como el gas se expande en el vacío, es decir que no lo hace contra fuerzas exteriores, y además las paredes del recipiente A y B son rígidas, el trabajo de expansión We también será cero, W_e= 0.

Como el proceso debe cumplir el primer principio de la Termodinámica podemos aplicar la ecuación: Q = ΔU + We y teniendo en cuenta que tanto Q como W_e son nulos:

ΔU=0 es decir que no hay variación de energía interna en el proceso.

El experimento de Joule fue objetado por su poca precisión, ya que la capacidad calorífica de sus recipientes y del agua eran mucho mayor que la del gas. Las investigaciones posteriores demostraron que debía observarse una variación de temperatura, lo cual indicaba que Q no era cero. Sin embargo resultó que cuando más se acercaba el gas al estado ideal tanto más pequeña era la diferencia de temperatura, lo cual hace suponer que en una expansión libre de un gas ideal Q debe ser cero. Podemos entonces enunciar la ley de Joule diciendo que la energía interna de un gas ideal no varia como resultado de una expansión libre.

Como ya vimos que la energía interna es función de dos cualquiera de las variables P, V y T, podemos considerar:

U = f(T,V) luego: (3)

Como en el experimento de joule hemos demostrado que U permanece constante, dU=0;

y como además T permanece constante dT= 0; entonces de la ecuación anterior deducimos que:

como dV ≠0, luego (4)

Esto quiere decir que la energía interna U, de un gas ideal, es independiente del volumen

Sí consideramos: U=f(T,P)

Como dU =0, dT =0, dP≠0 será:  

Significa entonces que en un gas ideal U no depende de P. Es evidente entonces que si la energía interna de un gas ideal no depende de P ni de V, será sólo función de la temperatura T. Esta conclusión tan importante, es otra forma de enunciar la Ley de Joule.

Para un proceso elemental sufrido por un sistema gaseoso cualquiera, la expresión diferencial del primer principio se puede escribir:

δQ=dU + P.dV (5)

reemplazando dU de la ecuación (3) en la (5)

Y como por la ecuación (1) reemplazando:

Esta ecuación, como ya dijimos, es válida para cualquier sistema gaseoso. Para un gas ideal, reemplazando (4) en (3) se cumplirá que:

y por la ecuación (1):

dU = C_V . dT (6)

Reemplazzndo (6) en la ecuación (5)

δQ = C_V.dT + P.dV (7)

Esta es la ecuación diferencial del primer principio aplicable a los gases ideales.

Por la ecuación (1) sabemos que , como para los gases ideales U no depende de V a temperatura constante, la ecuación (1) se puede escribir en la forma:

la cual nos indica que la capacidad calorífica a volumen constante de un gas ideal es independiente del volumen y de la presión del gas.

Veremos a continuación que los mismos resultados encontrados con la energía interna, son válidos respecto a la función entalpía.

Habíamos definido que: H = U + P.V (8)

derivando esta ecuación con respecto al volumen, a temperatura constante:

Para un gas ideal: y además:

luego (9)

Derivando la ecuación (8) con respecto a la presión a temperatura constante y por las mismas consideraciones anteriores, se deduce que: (10)

Las ecuaciones (9) y (10) nos indican que la entalpía de un gas ideal es independiente de su volumen y presión, o sea que depende solamente de la temperatura.

Si diferenciamos la ecuación (8)

dH = dU + P. dV+ V.dP

y de la ecuación (5), reemplazando:

dH = δQ + V.dP

o también: δQ = dH − V.dP (11)

Si hacemos H = f (T, P) ya vimos que: (12)

reemplazando la (12) en la (11) :

y por la ecuación (2) , reemplazando:

Esta ecuación es válida para cualquier sistema gaseoso. Si el gas es ideal, reemplazando la ecuación (10) en la (12):

y por la ecuación (2):

dH = C_P.dT (13)

Reemplazando la ecuación (13) en la (11):

δQ = C_P.dT − V.dP

Esta es la ecuación del primer principio tomando como parámetros T y P aplicable a los gases ideales.

Como para los gases ideales vimos que H no depende de P a temperatura constante, la ecuación (2) se puede escribir:

Esta ecuación indica que la capacidad calorífica a presión constante de un gas ideal, es independiente del volumen y de la presión del gas.