En 1960 Anderson y Cochran atribuyeron las transformaciones ferroeléctricas a la inestabilidad de las redes cristalinas con respecto a ciertas vibraciones de la red, los llamados modos suaves. Mucho antes, Fröhlich había asociado la frecuencia ωT de la vibración transversal de una red óptica, que aparece en la ecuación Lyddane - Sachs - Teller
ωT2 / ωL2 = ε∞ / εs
y los valores anormalmente altos de las constantes dieléctricas estáticas εs. Sin embargo, la aparición de un modo TO particularmente suave y la consecuente inestabilidad de la red si ωT → 0 cuando T → Tc+ se explica claramente por primera vez en 1960. En particular, Cochran atribuye la desaparición de las constantes de fuerza proporcional a ωT2 a la temperatura de transición Tc de los cristales iónicos a un equilibrio entre el corto alcance de las fuerzas repulsivas y atractivas fuerzas de Coulomb de largo alcance.
Las ecuaciones, que fueron presentados en una forma aplicable sólo a ciertos cristales cúbicos, se pueden generalizar a otras redes, y motivaron un número cada vez mayor de estudios espectroscópicos, utilizando la absorción infrarroja, la dispersión Raman, y la dispersión inelástica de neutrones, que confirmaron las predicciones teóricas. Chaves y Porto utilizaron una representación dependiente de la frecuencia de la función dieléctrica ε(ω) para generalizar la ecuación Lyddane - Sachs - Teller, incluyendo el caso de que la excitación de baja frecuencia dependiente de la temperatura responsable de la transformación tiene el carácter de una relajación:
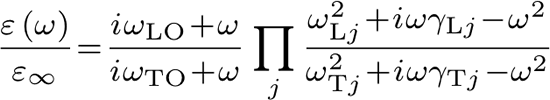
Aquí ωTO y ωLO representan las frecuencias transversales y de relajación longitudinal, respectivamente, y ωTj y ωLj las frecuencias características de las excitaciones oscilatorias longitudinales y transversales respectivamente. En fases ordenadas los cambios estructurales, en una primera aproximación, se pueden se identificados como los desplazamientos atómicos que se describen por el autovector del modo suave. Por el contrario, la suavización de un modo TO como una función de la temperatura se convirtió en evidencia para una transformación ferroeléctrica.
En ferroeléctricos propios el modo suave tiene un vector de onda q = 0 (punto Γ de la zona de Brillouin), ya que el parámetro de orden es la polarización homogénea. En ferroeléctricos impropios el correspondiente vector de onda q se encuentra dentro de, o en el límite de, la primera zona de Brillouin. Un ejemplo es el molibdato de gadolinio, Gd2 (MoO4)3. El vector de onda del modo perteneciente al parámetro de orden se encuentra en el límite de la zona de Brillouin; en consecuencia, por debajo de la temperatura de transición se duplica la unidad de celda. En este caso, la simetría del cristal permite una polarización proporcional a la magnitud del parámetro de orden de do componentes, así como una deformación. Las propiedades ferroeléctricas y ferroelástica resultantes de la fase ordenada fueron interpretadas correctamente por primera vez como los efectos de los parámetros de orden secundario por Pytte.
Por último, el caso de que la inestabilidad implique un modo suave para el cual el vector de onda qi se encuentre dentro de la primera zona de Brillouin se ejemplifica por el selenato de potasio, K2SeO4. Por medio de dispersión inelástica de neutrones, Iizumi et al. encontró en 1977 que qi = (1-δ (T)) c* / 3,
donde c* es un vector de la red recíproca. Por debajo de la transformación en Ti, la modulación impuesta a la red, con la condición de δ (T) «1, causa localmente que la celda unitaria aproximadamente se triplique. La modulación dependiente de la temperatura es inconmensurable con la red de fase desordenada y en el caso de selenato de potasio da lugar a una estructura localmente polar, pero globalmente centrosimétrica y por lo tanto no polar. El selenato de potasio se convierte en ferroeléctrico a una temperatura Tc < Ti cuando δ(T) → 0
y una fase conmensurable donde se forma una celda unitaria triplicada. La polarización homogénea puede ser vista como un parámetro de orden secundario que impulsa este proceso de lock-in.
Para una comprensión de las transformaciones ferroeléctricos, siempre han sido esenciales la determinación de estructuras de máxima precisión. Aunque se ha invertido un considerable esfuerzo en estudios de rayos X y difracción de neutrones, algunos aspectos cualitativos y cuantitativos siguen siendo no dilucidados, incluso para ferroeléctricos clásicos como el titanato de bario, ya que los cambios en las coordenadas atómicas son con frecuencia extremadamente pequeños. Si se conoce la simetría de las fases desordenada y ordenada, a menudo puede llevarse a cabo una descripción fenomenológica de un ferroeléctrico dentro de la precisión experimental sobre un intervalo de temperatura limitado por el recurso a métodos termodinámicos, pero no existe una teoría microscópica en general. El tratamiento de modelos especiales por los métodos de la teoría de las transiciones de fase ha tenido bastante éxito.