Newton fue el primero en explicar el movimiento, tanto de los cuerpos celestes —proporcionando la explicación matemática de las leyes observadas por Kepler para el movimiento de los planetas en órbitas elípticas—, como de los «terrestres» —la famosa caída de la manzana—, a partir de una única ley para las fuerzas: la ley de la gravitación universal. Anteriormente, los estudios y teorías de la mecánica habían buscado explicaciones separadas para ambos fenómenos. Kepler había deducido del análisis minucioso de las observaciones experimentales que los planetas describían elipses con foco en el Sol, así como la constancia de la velocidad areolar y el período de estos movimientos orbitales (aptdo. 5.5). A su vez, Galileo había caracterizado el movimiento de caída uniformemente acelerado de los graves, por —según la leyenda— experimentos desde la torre inclinada de Pisa. Todas estas descripciones eran empíricas, sin una justificación basada en modelos matemáticos coherentes.
La ley de la gravitación universal propuesta por Newton establece que entre dos cuerpos12 cualesquiera se produce una fuerza gravitatoria de atracción, proporcional al producto de las masas respectivas y al inverso del cuadrado de la distancia entre los mismos. La expresión de esta fuerza, en módulo, es
![]()
y en forma vectorial
![]() ; (1.3)
; (1.3)
donde F representa la fuerza ejercida por la masa M sobre m, y r es el vector que las une, con origen en M y extremo en m.
En la mecánica clásica, la fuerza gravitatoria es una acción a distancia que, de manera muy aproximada, podemos suponer se transmite de forma instantánea, sin necesitar de ningún medio material para ello. Así, cada masa M crea un campo de fuerzas gravitatorio, campo vectorial caracterizado en cada punto por una intensidad i:
![]()
La fuerza ejercida sobre un cuerpo de masa m será el producto de ésta por la intensidad del campo,
![]()
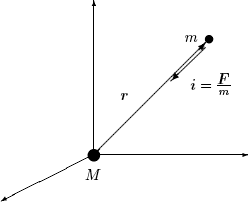
Figura 1.3: Atracción gravitatoria entre dos masas M y m, situadas a distancia r
La teoría de la relatividad general elimina las fuerzas gravitatorias; para ello, interpreta el efecto de las masas como una modificación a la métrica espacio-tiempo, que resulta ser Riemanniana en lugar de Euclídea. Así, en esta nueva métrica, las trayectorias de las partículas corresponden a las geodésicas del espacio-tiempo, que vendrían a ser las ecuaciones horarias del movimiento13.
1.6.1. Masa Gravitatoria y Masa Inerte.
En principio, el concepto de masa que interviene en la ley de la gravitación no tendría porqué coincidir con la masa empleada para la ley II de Newton; en el primer caso sirve para definir la fuerza gravitatoria, mientras que en el segundo define la fuerza de inercia. Podemos distinguirlas por tanto denominándolas mg (masa gravitatoria) y mi (masa inerte).
Existe, sin embargo, una observación experimental: en la superficie de la tierra todos los cuerpos caen en el vacío hacia el suelo con la misma aceleración (g). Sea un cuerpo cualquiera en la superficie de la tierra; su peso es
![]()
donde Mg y mg son las masas respectivas (gravitatorias) de la Tierra y del cuerpo, R es el radio de la tierra (suponemos el cuerpo a una altura h pequeña, por lo que R + h ô R), y G es la constante de la gravitación universal.
Empleando la segunda ley de Newton, se puede relacionar el peso con la aceleración que experimenta el cuerpo:
w = mig;
siendo mi la masa (inercial) del mismo. Igualando ambas expresiones de w se obtiene:
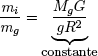
Así, el cociente mi/mg permanece constante. Ya que G es una constante cuyo valor puede ser cualquiera, es posible elegir el mismo de forma que este cociente sea la unidad. De esta forma, ambas masas tendrían siempre igual valor:
mi ≡ mg
Para ello, el valor de la constante de la gravitación universal ha de ser
![]()
Consideraciones sobre el universo.— Supongamos que el universo tiene un tamaño finito, y que, de forma aproximada, se puede idealizar como una esfera, con una distribución de masa de densidad media r. Sea un cuerpo de masa m, situado a una distancia R del centro de dicha esfera; este experimentaría una fuerza atractiva hacia el centro del universo de valor:
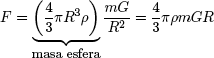
Así, todos los cuerpos del universo experimentarán una aceleración hacia el centro de aquél de valor creciente proporcionalmente a su distancia R. Si esto fuese así, desde un punto distinto del centro del universo se observaría un movimiento diferente de las estrellas y galaxias según las distintas direcciones de observación; en la dirección del radio creciente, la aceleración sería mayor, mientras que en la opuesta disminuiría. Sin embargo, esto no parece concordar con las observaciones experimentales medidas desde la Tierra.
¿Cómo se puede explicar esto, admitiendo que el universo es finito?
Una posible explicación sería una teoría «antropocéntrica», según la que el planeta Tierra tendría el inmenso privilegio de estar situado justo en el centro del universo. De esta forma, nuestras observaciones deberían ser iguales en cualquier dirección, ya que todas serían radiales. Sin embargo, fuera de creencias pseudo-religiosas, la teoría antropocéntrica parece poco probable. Más bien, la observación anterior podría explicarse por una de las siguientes dos hipótesis:
1. El universo es homogéneo, isótropo e infinito. Sin embargo, esta suposición es incompatible con la teoría, generalmente aceptada en la actualidad, del «Big-Bang» como origen del universo. Esta primera explosión primigenia ocurrió al parecer hace unos diez mil millones de años, lo que establece un límite para el tamaño del universo.
2. El universo es finito, pero con una métrica no euclídea, en la que todos los puntos pueden considerarse el centro de los demás. Esta última hipótesis es la que parece más plausible, quedando por discutir el tipo de métrica, para lo cual existen a su vez distintas teorías.
E. Mach interpretó la acción gravitatoria del resto del universo como responsable de la inercia de los cuerpos. Así, sería la masa del universo lejano la encargada de mantener un cuerpo con velocidad uniforme y rectilínea o en reposo ante la ausencia de otras fuerzas cercanas. Esto podría ser una bonita teoría, pero Mach lo dejó planteado tan sólo como una especulación, que carece de una justificación rigurosa.
Tipos de fuerzas en el universo
Las fuerzas gravitatorias no son las únicas que existen en el universo físico. De forma esquemática se pueden distinguir cuatro tipos fundamentales de fuerzas, siendo las demás manifestaciones macroscópicas de éstas.
1. Fuerzas gravitatorias.
Aunque en la mecánica clásica se consideran como acciones a distancia, de propagación instantánea, en la realidad parece que se propagan con velocidad finita. Esta propagación se realiza mediante las llamadas ondas gravitatorias. En la interpretación dual onda/corpúsculo equivalen a las partículas llamadas Gravitones14.
2. Fuerzas electromagnéticas.
Están gobernadas por las ecuaciones de Maxwell del campo electromagnético. Se propagan mediante las Ondas electromagnéticas, que incluyen la luz, ondas de radio, etc. Las partículas equivalentes son los Fotones.
3. Fuerzas nucleares fuertes.
Son las fuerzas que unen a las partículas en el núcleo atómico. Intervienen únicamente en la mecánica cuántica. Están asociadas a las partículas denominadas Gluones.
4. Fuerzas nucleares débiles.
Son las fuerzas que intervienen en la desintegración nuclear. Asimismo intervienen en la mecánica cuántica, y las partículas asociadas son los Bosones.
La publicación por Newton de los «Principia» con la teoría de la gravitación universal supuso en su tiempo un avance importante para la mecánica y para las matemáticas, al interpretar de forma coherente y unificada dos tipos de fenómenos que antes se consideraban obedecientes a leyes distintas: el movimiento de los objetos terrestres y el de los objetos celestes. De manera similar, se busca hoy en día, por parte de los físicos teóricos y matemáticos, una teoría unificada que permita explicar, a partir de una causa común, los cuatro tipos de fuerzas que se observan en el universo. Sin embargo, es de prever que esta teoría, aún en el improbable caso de poderse obtener, sería mucho más compleja y engorrosa de utilizar que la mecánica clásica o los métodos newtonianos. Por ello, aún en la hipótesis de que se logre algún avance importante en esta línea, es improbable que tenga repercusiones prácticas en la mecánica aplicada a la ingeniería, campo que nos ocupa y en el cual la mecánica clásica seguirá teniendo plena vigencia.
11. No debe originar confusión la existencia de dos unidades con el mismo nombre para caracterizar magnitudes distintas: el kg de masa, y el kg de fuerza o kilopondio (kp), definido como el peso de 1 kg de masa en la superficie de la tierra, considerando un valor medio constante de la aceleración de la gravedad (1 kg fuerza ' 9;81 N). Ello permite hablar —afortunadamente para los tenderos, fruteros, pescaderos y demás gremios poco interesados en la filosofía de la mecánica durante su quehacer cotidiano— simplemente de kg, sin necesitar especificar si se trata de masa o de peso, ya que en la superficie de la tierra ambos son equivalentes, al menos en una primera aproximación en que g se suponga constante.
12 Debe entenderse _cuerpo_ en el sentido de partícula, tal y como emplea Newton este término (Aptdo. 1.4.).
13. En la mecánica clásica la trayectoria seguida por una partícula sometida a la acción gravitatoria de otra es una cónica, como se verá en el capítulo 5. Podríamos –plantearnos en la teoría de la relatividad general, qué trayectoria seguiría un cuerpo en un universo homogéneo, pero en cualquier caso no resulta ser una cónica. En un caso sencillo, con una única masa aislada, la métrica de Schwarzschild creada por ésta conduce a órbitas que no se cierran, lo que puede explicar algunos fenómenos bien conocidos como el corrimiento del perihelio de Mercurio.
14. Aunque se han establecido diversos experimentos para detectar las ondas gravitatorias, aún no se han llegado a medir de forma fehaciente, debido a su intensidad extremadamente baja.