El principio de la relatividad galileana4 establece que:
‘Dos sistemas de referencia en movimiento relativo de traslación rectilínea uniforme son equivalentes desde el punto de vista mecánico; es decir, los experimentos mecánicos se desarrollan de igual manera en ambos, y las leyes de la mecánica son las mismas.’
Uno de los ejemplos puestos por Galileo es el de un observador viajando en un barco que navega plácidamente sobre un río, en contraste con un observador fijo en la orilla. Ambos interpretan de la misma manera la caída de un cuerpo hacia el suelo en su propio sistema, que como sabemos sigue un movimiento vertical uniformemente acelerado.
Transformación de Galileo5.— Sea un sistema móvil (O’x’y’z’), que se traslada respecto a otro fijo (Oxyz) con velocidad v, manteniéndose paralelos los ejes de ambos. Puesto que podemos elegir las direcciones del triedro
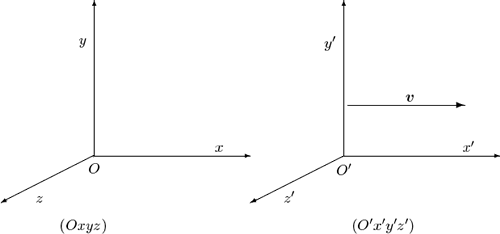
Figura 1.1: Sistemas de referencia en movimiento relativo rectilíneo y uniforme, con velocidad v en la dirección de Ox
de referencia, elegimos la dirección Ox según la dirección de la velocidad de traslación (recordemos que el espacio es es isótropo, por lo que es lícito elegir una orientación arbitraria para los ejes, sin pérdida de generalidad).
Consideraremos también que Inicialmente (para t = 0) O y O’ coinciden. Sean (x; y; z) las coordenadas de un punto en el sistema fijo, (x’; y’; z’) en el móvil y v el módulo de la velocidad. Las ecuaciones de transformación para las coordenadas son:
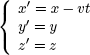
Derivando sucesivamente6, obtenemos las velocidades y aceleraciones en ambos sistemas:
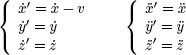
Se observa por tanto que las derivadas segundas (aceleraciones) coinciden. Esto nos permite intuir —admitiendo como postulado el principio de la relatividad galileana— que las leyes de la dinámica están basadas en las derivadas segundas respecto al tiempo, única forma de que las leyes sean invariantes cumpliéndose dicho principio. En efecto, según sabemos, el estado de un sistema formado por un partícula en movimiento según una dirección fija se caracteriza en un instante dado por su posición y su velocidad (x; x˙). La evolución del movimiento viene gobernada por la ecuación dinámica (F = mx¨).
4. Galileo Galilei, Discursos y demostraciones en torno a dos ciencias nuevas relacionadas con la mecánica, 1602. Galileo, que vivió entre 1564 y 1642, realizó contribuciones importantes a la mecánica y a la astronomía, estudiando por primera vez los cielos mediante el telescopio que diseñó él mismo. Fue condenado como hereje por la inquisición católica, que no aceptaba su teoría según la cual la tierra gira alrededor del sol.
5. En el apartado 6.3.5 se ofrece una generalización de esta transformación y se discute la relación de las simetrías que expresa (invariancias cuando se produce la transformación) con las constantes del movimiento y los principios de conservación.
6. En lo sucesivo se empleará la notación de uno o dos puntos superpuestos para indicar derivadas (totales) respecto al tiempo: x˙ =(def) dx/dt, x¨ =(def) d2x/dt2. También emplearemos la notación mediante negritas para identificar vectores o tensores: a ≡ {ai}, I º [Ikl].