La propagación se realiza cuando un rayo de luz ingresa al núcleo de la fibra óptica y dentro de él se producen sucesivas reflexiones en la superficie de separación núcleo – revestimiento.
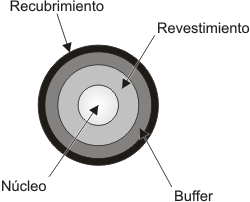
La condición más importante para que la fibra óptica pueda confinar la luz en el núcleo y guiarla es:
n 1 > n 2
Para describir los mecanismos de propagación se usará la óptica geométrica. Se basa en que la luz se considera como rayos angostos, donde la reflexión ocurre en la frontera de dos materiales de índices de refracción diferentes.
En el vacío las ondas electromagnéticas se propagan con la velocidad de la luz 299.792.456 km/seg.
En el aire se puede aproximar a:
c = 300,000 km/seg.
Si se tiene un material con distinto índice de refracción al del aire, su velocidad será ligeramente distinta a la de la luz dependiente de n
![]()
Relación que puede escribirse ![]()
donde:
c = es la velocidad de la luz (3.000.000.000 m/s) en el aire
v = es la velocidad de la luz en un material especifico.
n = índice de refracción
Cuando un rayo incide en la frontera entre dos medios con diferentes índices de refracción, el rayo incidente será refractado con distinto ángulo, según la ley de refracción de Snell,
![]()
De donde
n2sen θ2 = n1sen θ1
n1= índice de refracción del material 1 (adimensional)
n2= índice de refracción del material 2 (adimensional)
θ1= es el ángulo de incidencia (grados)
θ2 = es el ángulo de refracción (grados)
v1 = velocidad en el material 1
v2 = velocidad en el material 2
La representación de la ley de Snell se muestra en la figura que se encuentra a continuación.
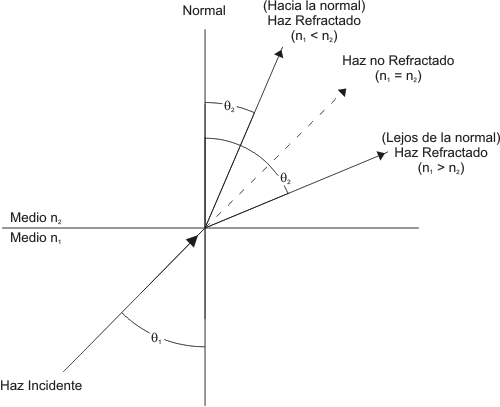
En la frontera, el haz incidente se refracta hacia la normal o lejos de ella, dependiendo si n1 es menor o mayor que n2.
Esto implica que si un rayo ingresa de un medio menos denso (índice refractivo más bajo) a otro más denso (índice refractivo mas alto) (n1< n2), el rayo se refracta con un ángulo menor con respecto a la perpendicular de la frontera.
En el caso contrario cuando un rayo incide de un medio más denso hacia otro menos denso, el rayo se refracta con un ángulo mayor con respecto a la perpendicular de la frontera.
Ángulo crítico
Puesto que los rayos se alejan de la normal cuando entran en un medio menos denso, el ángulo de incidencia, denominado ángulo crítico, resulta cuando el rayo refractado forma un ángulo de 90º con la normal, (superficie de separación entre ambos medios). Si el ángulo de incidencia se hace mayor que el ángulo crítico, los rayos de luz serán totalmente reflejados.
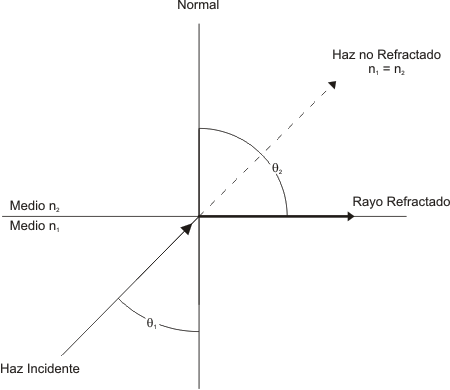
Por Snell
n2sen θ2 = n1sen θ1
Si θ2 = 90º
θ1 = θC= ángulo crítico
![]()
Entonces para θ1 > θC => reflexión total
Índices de refracción de varios materiales se indican en la siguiente tabla.
MEDIO |
INDICE DE REFRACCION |
|---|---|
| Vacío |
1.0
|
| Aire |
1.0003
|
| Agua |
1.33
|
| Alcohol etílico |
1.36
|
| Cuarzo fundido |
1.46
|
| Fibra de vidrio |
1.5-1.9
|
| Diamante |
2.0-2.42
|
| Silicio |
3.4
|
| Galio Arsenuro |
3.6
|
El ángulo crítico considerando el aire y el vidrio será:
Para el aire n2 =1
Vidrio n1 = 1.5
1.5 sen θ1 = 1
θ1 = 41.8º
Ejemplo
Si el medio 1 es vidrio y el medio 2 alcohol etílico. Para un ángulo de incidencia de 30°, determine el ángulo de refracción.
De la tabla
n1 (vidrio) = 1.5
n2 (alcohol etílico) = 1.36