Errores accidentales
Es un hecho que efectuadas mediciones repetidas por un observador usando el mismo método y en iguales condiciones, no llega a obtener idénticos resultados. Las mediciones realizadas estarán entre otras cosas siempre afectadas por perturbaciones del medio ambiente que escapan del control impuesto.
Contrariamente aquellas hipótesis, la igualdad de condiciones no existe debido a la variación imprevista de la calibración de los instrumentos (inestabilidad en la calibración) como así también a la alteración en la sensibilidad de los sentidos (imperfección humana). Todas esas causas de características aleatorias, darán origen a los denominados errores accidentales.
Si bien el medio ambiente produce en general efectos sistemáticos, la superposición de ellos, sin perder su naturaleza individual, juega en el transcurso de la medición de una manera tal que el efecto combinado no sigue una ley sencilla, por lo tanto al no efectuarse la respectiva corrección, por ser dificultosa e incierta, su variación quedaran incluidas como componentes del error accidental.
Resumiendo, se puede expresar que la característica fundamental de los errores accidentales, es que no se repiten en un solo sentido, significando esto que pueden tener valores numéricos iguales pero de distintos signos.
En consecuencia, siendo esta propiedad común a todos los errores de este tipo, indeterminación en su signo, se lo engloba en una ley de carácter probabilística como después se ha de estudiar.
El análisis basado en estos fundamentos permitirá introducir el concepto en la teoría de errores de la llamada precisión de las mediciones o de los instrumentos.
Error de lectura
Cuando se habla de lectura de un instrumento de medida indicador, se quiere significar la referencia de la posición relativa del índice y de la graduación, en esta apreciaciones se comete un error de lectura debido a las siguientes causas.
Paralaje
Como la aguja A se mueve a cierta distancia “m” del plano de la escala E, se produce el error de paralaje Δl cuando la visual del operador O no es perpendicular a dicho plano, sino que forma un ángulo +/-β con la vertical, el ángulo se de observación, resulta como expresión del error de paralaje
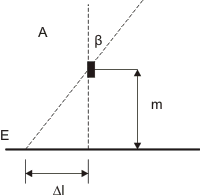
Δl = +/- m . tg β
Para m = 2mm y β = +/- 6º
Δl = +/- 2mm . tg 6º = +/- 0,2 mm
Error debido al límite del poder separador del ojo humano
Se sabe que en condiciones normales de visibilidad la distancia angular mínima necesaria para observar dos puntos A y B separados según la figura, es de 2 minutos.
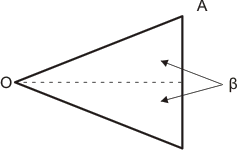
En general, las escalas son, leídas desde una distancia media de aproximadamente 250 mm.
Propongámonos hallar cual es aquella distancia, la separación mínima entre los puntos A y B de manera que loS mismo se observen aun distintos o separados; vale decir, cual es el valor de la distancia AB para que el ángulo AOB valga 2´.
De la figura, se tiene: AC =. OC . tg β/2 y AB = 2 . AC = 2 . OC . tg β/2 = 2 . 250 mm . tg 1´
Siendo : tg 1´= 0,000291
Será AB = 0,15 mm
Podemos entonces asegurar Que un ojo normal podrá observar dos puntos situados a una distancia igual a 250 mm. de su pupila, en forma perfectamente distinta siempre que los mismos se encuentren a una distancia igual o mayor que 0,15 mm.
Yendo a nuestro caso práctico, entonces, si suponemos por ejemplo que el punto A representa el extremo del índice del instrumento, y el B el punto de la escala que suponemos corresponde a dicho extremo del índice, podrá haber entre dichos puntos una separación de 0,15 mm, y sin embargo los consideramos coincidentes.
Se comprende que este error, puede ser indistintamente en más o en menos, y, por otra parte, dado su carácter fisiológico, no es tampoco una magnitud constante.
De aquí su clasificación como error accidental.
El error de estimación o de apreciación
El error de estimación o de apreciación se confunde a veces can el error debido al poder separador del ojo humano, pero en realidad deben ambos interpretarse como errores de origen distintos.
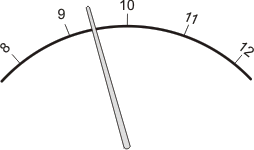
El error de apreciación se comete al leer valor de la desviación encontrándose la aguja entre dos divisiones sucesivas de la escala; en este caso existe cierta incertidumbre en la apreciación de la posición exacta de la aguja sobre la escala, incertidumbre que no se hace leer indistintamente mayor o menor que el verdadero y en una cantidad representada por la menor fracción que puede apreciarse de la división considerada sobre la escala.
De aquí sometida esta desviación a la lectura por distintos observadores, los valores registrados por cada uno de ellos no coinciden generalmente.
La apreciación de la fracción de división difiere de uno a otro, aun cuando el poder separador visual fuera igual para todos ellos.
Es por lo tanto un factor personal en el cual juega un rol importante la experiencia y habilidad del operador en esta clase de lecturas, y de ciertos detalles constructivos del instrumento como el espesor del índice, espesor y separación de los trazos de la escala, etc.
El error de apreciación puede reducirse acercando más las divisiones de la escala y tratando, cuando la medida lo permita, de hacerse coincidir el índice con una de las divisiones.
Error de lectura:
- Error de paralaje
- Error debido al límite del poder separador del ojo humano
- Error de estimación
En general, el error absoluto de lectura Δα varía entre 1/10 y 1/5 de división de la escala de medida, estimándose como valor practico:
Δα = 0,25 mm