Formuladas por Isaac Newton en su obra «Philosophiae Naturalis Principia Matematica» (1686), constituyen el primer intento de formular una base axiomática para una teoría científica de la mecánica. Debe aclararse que no fueron formuladas por Newton de forma precisa como se suelen recoger hoy en día en los libros de texto. También debe advertirse que en sentido riguroso no recogen de forma completa toda la axiomática necesaria para la mecánica clásica, siendo necesario incorporar aportaciones adicionales de Euler, Cauchy y otros. A pesar de esto, la publicación de los «principia» constituye un hito monumental de enorme valor, sobre el que se cimienta la mecánica clásica.
Para aclarar el modelo axiomático de Newton citaremos aquí textualmente de los «Principia»7. Newton parte en primer lugar de cuatro definiciones:
DEFINICION PRIMERA.
‘La cantidad de materia es la medida de la misma originada de su densidad y volumen conjuntamente.’
DEFINICION II.
‘La cantidad de movimiento es la medida del mismo obtenida de la velocidad y de la cantidad de material conjuntamente.’
DEFINICION III.
‘La fuerza ínsita de la materia es una capacidad de resistir por la que cualquier cuerpo, por cuanto de él depende, perservera en su estado de reposo o movimiento uniforme y rectilíneo.’
DEFINICION IV.
‘La fuerza impresa es la acción ejercida sobre un cuerpo para cambiar su estado de reposo o movimiento uniforme y rectilíneo.’
La definición primera (cantidad de materia de un cuerpo) equivale a lo que conocemos por masa. La tercera caracteriza las denominadas fuerzas de inercia, mientras que la cuarta se refiere a las fuerzas propiamente dichas. Realizadas estas definiciones, Newton enuncia sus conocidas tres leyes o principios fundamentales:
LEY PRIMERA.
‘Todo cuerpo persevera en su estado de reposo o movimiento rectilíneo y uniforme a no ser en tanto que sea obligado por fuerzas impresas a cambiar su estado.’
Esta ley constituye el llamado principio de la inercia. Admitiendo también el principio de Galileo, nos permite definir los llamados sistemas inerciales, como aquellos en los que se cumple dicho principio. Las leyes de la mecánica se formulan en un sistema inercial de referencia. Por el principio de Galileo, admitiendo que existe al menos un tal sistema inercial, existirán infinitos sistemas inerciales en los que se cumplen las mismas leyes mecánicas y en concreto la ley primera de Newton: todos aquellos relacionados entre sí mediante transformaciones de Galileo (1.1), es decir, que se mueven con velocidad rectilínea y uniforme respecto al primero.
Este principio nos permite también definir, como condiciones
iniciales del movimiento, las que caracterizan a un movimiento estacionario o
constante: la posición r y la velocidad ![]()
Conviene observar también que Newton emplea el término «cuerpo» para referirse en realidad a una partícula, o punto material, caracterizada por la posición y velocidad de un solo punto8.
LEY SEGUNDA
‘El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.’
Esta ley indica claramente una relación lineal («proporcional») entre fuerzas y variaciones de la cantidad de movimiento, de tipo vectorial («según la línea recta»). Se denomina en ocasiones ley fundamental de la dinámica, permitiendo obtener las ecuaciones básicas de la misma. Expresada como ecuación, equivale a:
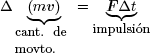
Pasando al límite, para un incremento infinitesimal de tiempo, obtenemos la relación diferencial siguiente:
d(mv) = Fdt:
O bien, llamando cantidad de movimiento a ![]() ,
,
Admitiremos en principio que la masa de un cuerpo se conserva. Así pues,
se llega a la conocida expresión que define la ley del movimiento de una
partícula:
F = ma; (1.2)
donde ![]() . Cabe realizar en
relación con esta fórmula las siguientes Observaciones:
. Cabe realizar en
relación con esta fórmula las siguientes Observaciones:
- La aceleración, derivada segunda del vector posición, es asimismo un vector. La ecuación (1.2) tiene por tanto carácter vectorial, lo que identifica a las fuerzas como vectores, e implícitamente supone la aditividad vectorial para las mismas (ley del paralelogramo de fuerzas).
- La expresión (1.2) da lugar a ecuaciones diferenciales de segundo orden, ya que intervienen derivadas segundas de la incógnita r respecto al tiempo.
LEY TERCERA
‘Con toda acción ocurre siempre una reacción igual y contraria. O sea, las acciones mutuas de los cuerpos siempre son iguales y dirigidas en direcciones opuestas.’
Se trata del llamado principio de acción y reacción. Todas las fuerzas deben de tener contrapartida, siendo imposible ejercer una fuerza desde el vacío, sin apoyo. Es siempre necesario apoyarse en algún cuerpo o medio material que absorba la reacción (modificando a su vez el movimiento de este otro cuerpo, según la segunda ley).
Ejemplo 1.1:
Fuerza ejercida desde la superficie de la Tierra. Todo cuerpo cercano a la tierra, tanto en estado de movimiento (caída libre) o en reposo sobre el suelo, recibe una fuerza (denominada peso) ejercida por la tierra, que lo mueve en el primer caso o lo mantiene inmóvil en el segundo. El cuerpo a su vez ejerce sobre la tierra una fuerza igual y contraria, aunque esta última, debido a la gran masa de la tierra, produce un efecto muy pequeño sobre nuestro planeta.
Ejemplo 1.2:
Movimiento de un cohete en el vacío. Una fuerza no se puede ejercer sobre el vacío, necesitando siempre aplicarse sobre otro cuerpo (que a su vez producirá una reacción igual sobre el primero). Para moverse —o más bien acelerar o frenar, es decir, variar el movimiento— en el vacío, un cohete o sonda espacial necesita apoyarse sobre algún medio. Esto se consigue mediante masa expulsada por la tobera, medio en el cual se apoya el cohete, a través de la expulsión de los gases del combustible quemado, propulsión iónica, plasma, u otros medios. De este tema se tratará en el capítulo 6.6.
7. Las citas han sido extraídas de Isaac Newton, Principios Matemáticos de la Filosofía Natural (2 tomos), traducción espa˜nola de Eloy Rada, Alianza Editorial, 1987.
8 El tratamiento de los sólidos rígidos, así como el de sistemas generales formados por varias partículas, requiere de diversos principios y teoremas adicionales que fueron propuestos por L. Euler. De esto se tratará en los capítulos 6 y 8.