2.1. Principios y Teoremas Generales

2.1.1. Cantidad de Movimiento

Se llama cantidad de movimiento¹ de una partícula a

El principio de la cantidad de movimiento se deduce como consecuencia directa de la segunda ley de Newton (1.4):

En el caso usual de que la masa de la partícula no varíe², se obtiene la expresión clásica de la ley fundamental de la dinámica (1.2), Fuerza = masa x aceleración:

(2.2)

Conviene recordar que, en esta expresión, F representa la resultante de todas las fuerzas aplicadas sobre la partícula. Se deben incluir, mediante suma vectorial, tanto las fuerzas activas como las reacciones de apoyo o reacciones del medio.

Cuando la fuerza total se anula, se obtiene el correspondiente teorema de conservación:

si F = 0; p = cte. (2.3)

Por lo tanto, el movimiento de una partícula aislada es tal que se conserva su cantidad de movimiento; es decir, su velocidad se mantiene constante, describiendo un movimiento rectilíneo uniforme.

2.1.2. Momento Cinético

Sea una partícula m, dotada de una velocidad v y situada en un punto P. El momento cinético³ respecto a un punto fijo O, H_O⁴, se define como el momento de la cantidad de movimiento respecto a dicho punto. Tomando O como origen del sistema de referencia (inercial) Oxyz,

derivando respecto del tiempo:

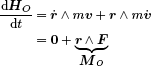
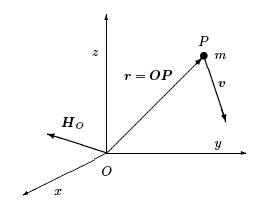
Figura 2.2: Momento cinético de una partícula respecto al punto O.

siendo el momento de la fuerza F respecto a O. Resulta por tanto la ecuación:

(2.4)

El correspondiente teorema de conservación que se deduce de (2.4) es:

si M_O= 0, H_O= cte: (2.5)

Esta conservación se verificará en el caso de la partícula aislada, y también en el caso de fuerzas centrales que se describe más abajo.

Momento áxico

Figura 2.3: Momento áxico respecto a un eje (O; e)

Sea un eje de dirección fija e, pasando por el punto O. Se define como momento áxico respecto de este eje la proyección del momento cinético respecto de un punto cualquiera del eje sobre la dirección del mismo. Empleando la notación

multiplicando escalarmente ambos miembros de (2.4) por e se deduce directamente la igualdad:

Esta fórmula se puede aplicar entre otros casos al movimiento plano de rotación alrededor de un eje fijo.

Fuerzas centrales

Se denominan centrales a las fuerzas que pasan constantemente por un punto dado, «centro» de las fuerzas. Es evidente que respecto de este punto el momento de las fuerzas es nulo, por lo que aplicando (2.5) se deduce que el momento cinético se conserva:

H_O= cte.

Se obtienen inmediatamente 2 características importantes del movimiento:

1. La trayectoria es plana;

ya que al ser H_O= r^mv, r es constantemente perpendicular a una dirección H_Ofija, definiendo por tanto un plano.

2. La velocidad areolar es constante;

puesto que el área barrida por unidad de tiempo (figura 2.4) es:

Figura 2.4: Fuerzas centrales, dirigidas hacia un centro de fuerzas O. El área barrida en el intervalo infinitesimal dt es dS = OPP' = ½ | r ∧ dr |

2.1.3. Energía Cinética

Sea una partícula de masa m, que se mueve según una trayectoria Γ, bajo la acción de fuerzas con resultante F (recordemos que ésta incluye todas las fuerzas, activas y pasivas). El trabajo elemental realizado por F en un desplazamiento infinitesimal dr se define por el producto escalar siguiente⁵

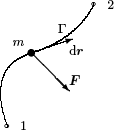
Figura 2.5: Trabajo realizado por F al recorrer la curva Γ entre 1 y 2.

F en un desplazamiento infinitesimal dr se define por el producto escalar Siguiente

considerando que F = mdv=dt y dr = vdt,

(2.6)

El trabajo realizado al recorrer Γ entre los dos puntos extremos 1 y 2 resulta de la integral curvilínea:

Se define como energía cinética T de la partícula:

así, la expresión anterior equivale a

W₁₂ = T₂ €− T₁(2.7)

Podemos enunciar entonces:

‘El trabajo realizado por la resultante de las fuerzas sobre una partícula es igual al incremento de su energía cinética.’

Este resultado se suele llamar también el teorema de las fuerzas vivas.

Caso de fuerzas conservativas

Se denomina campo de fuerzas conservativas aquél en el que el trabajo realizado por la fuerza, para recorrer el camino entre dos puntos dados, es independiente de la trayectoria seguida Ä para ir de uno al otro. Así para distintos caminos Γ₁, Γ₂, Γ₃ que tengan en común el origen (1) y el final (2).

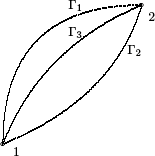
Figura 2.6: Trayectorias distintas en un campo conservativo para ir de 1 a 2.

Es fácil ver que esta condición es equivalente a que el trabajo realizado para recorrer cualquier trayectoria cerrada sea nulo. En efecto, sea una curva cerrada cualquiera Ä, a la que pertenecen los puntos 1 y 2. ésta puede descomponerse en dos curvas abiertas con extremos en 1 y 2: Γ = Γ⁺₁∪ Γ^–₂ , teniendo Γ⁺₁ el sentido de 1 a 2 y Γ^–₂ el sentido de 2 a 1. La integral curvilínea sobre Γ es pues

como queríamos demostrar.

(2.8)

No son conservativas las fuerzas debidas a resistencias pasivas, como el rozamiento o las fuerzas de tipo viscoso. En éstas el integrando (F Γ dr) es siempre negativo, puesto que la fuerza de resistencia (F) se opone al movimiento (dr), por lo que la integral (2.8) no se puede anular nunca. Se produce necesariamente una disipación de energía, no pudiendo recobrarse el nivel energético inicial después de un trayecto cerrado.

Un teorema básico del cálculo vectorial establece que la condición necesaria y suficiente para que un campo vectorial F tenga circulación nula para cualquier curva cerrada es que sea un campo de gradientes. Recordemos en primer lugar la definición de gradiente de un campo escalar; en un sistema de coordenadas cartesianas ortonormal con versores {e_i} ≡ {i; j; k} la expresión es⁶

La afirmación anterior quiere decir que existirá un campo escalar V (r), función de la posición, tal que:

F =–grad V.

Al campo escalar V se le denomina potencial de las fuerzas, energía potencial, o simplemente potencial.

Una tercera forma de caracterizar un campo F como conservativo, admitiendo las exigencias adicionales de que F tenga derivada continua y que el dominio sea simplemente conexo, es que sea irrotacional. Esta condición es equivalente a su vez a las dos anteriores. Recordemos la definición de rotacional de un campo vectorial⁷:

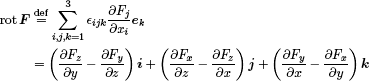
Por lo que la condición para que el campo F sea conservativo es

rot F = 0: (2.9)

En este caso, la función potencial V (r) de la que proviene F debe ser al menos C².

Al expresarse F como un gradiente, el trabajo elemental resulta ser una

diferencial exacta:

F · dr = –grad V · dr = –dV

Si integramos para obtener el trabajo realizado entre dos puntos 1 y 2, y empleando el principio de la energía cinética (2.7):

es decir, se conserva la suma de la energía cinética más la potencial:

T₁ + V₁ = T₂ + V₂

o bien, definiendo como energía total⁸ a la suma de energía cinética y potencial,

se obtiene la siguiente expresión para el teorema de conservación de la energía:

si F =–grad V (conservativa), E = T + V = cte. (2.10)

En lo anterior se ha supuesto que el potencial V (r) es constante. Pudiera darse el caso de que F provenga de una función potencial no constante, es decir que dependa explícitamente del tiempo, V (r; t):

En este caso, no se conservaría la energía total E, puesto que el trabajo elemental ya no sería una diferencial exacta del potencial:

Estaríamos, pues, ante un campo de fuerzas no conservativas a pesar de que provengan de un potencial.

Integración de la ecuación fundamental de la dinámica.

Parte de lo expuesto arriba se puede interpretar como distintos procedimientos de integración de la ecuación fundamental de la dinámica (2.2). Señalemos tres procedimientos generales para ello, que permiten obtener los teoremas de conservación (2.3), (2.5) y (2.10) como casos particulares.

Integración directa en el tiempo

Integrando entre dos instantes t₁ y t₂,

se obtiene la ecuación del balance de la cantidad de movimiento,

Como caso particular de esta ecuación de balance se desprende el teorema de conservación de la cantidad de movimiento (2.3)

Integración directa según la trayectoria

Realizando ahora la integral curvilínea entre dos puntos de la trayectoria r₁ y r₂,

de donde se obtiene la ecuación del balance de la energía,

Análogamente, para el caso de fuerzas conservativas (F = –gradV ), se desprende el teorema de conservación (2.10).

Integración del momento en el tiempo

Integrando el momento de F entre dos instantes t₁ y t₂,

se obtiene la ecuación del balance del momento cinético,

Si las fuerzas son centrales o se trata de una partícula aislada, análogamente a los dos casos anteriores se desprende el teorema de conservación (2.5).

1. En Inglés se emplea el término «linear momentum» o simplemente «momentum», por lo que algunos autores emplean el término momento lineal (traducción literal del inglés) en lugar de cantidad de movimiento.

2. Estrictamente hablando, la masa de una partícula es siempre invariable; al hablar de casos en los que m sea variable, nos referimos a cuerpos que pierdan o ganen partículas de masa (ver capítulo 6.6).

3. En las traducciones literales de la terminología anglosajona se emplea el término momento angular.

4. Otros autores emplean notaciones distintas para referirse al momento cinético: OK (M. Roy, Fernández Palacios), L_O(Marion, Goldstein, Griffiths)

5. La notación empleada, «dW», no indica aquí una diferencial exacta de una determinada función W, sino únicamente un incremento infinitesimal de trabajo producido por F a lo largo de dr. Tan sólo resulta ser una diferencial exacta cuando las fuerzas son conservativas.

6. En cuanto a notación, emplearemos indistintamente los índices o los _nombres propios _ de vectores (i ≡e₁; j ≡e₂; k ≡e₃) y coordenadas (x ≡ x1; y ≡ x2; z ≡ x3). Asimismo, a veces emplearemos también notaciones alternativas para el gradiente, grad V = dV=dr = ∇V , empleando el operador ∇ = ∑ ³_i=1∂/∂x_ie_i= ∂/∂x i + ∂/∂y j + ∂/∂z k.

7. Empleando el operador ∇, el rotacional se puede expresar también mediante la notación rot F = ∇^ F.

8. Se sobreentiende que ésta es únicamente la energía mecánica , excluyendo a otros tipos de energía como la calorífica, química, . . .