Velocidad de modulación
Se define como la inversa del tiempo más corto entre dos instantes significativos de la señal.
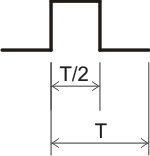
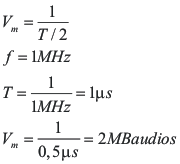
Esta velocidad está dada por la velocidad de cambio de la señal y por lo tanto dependerá del esquema de codificación elegido.
Velocidad de transmisión
Está dada por la cantidad de bits que se transmiten por segundo independientemente de si los mismos contienen información o no.
La velocidad de transmisión esta dada por:
![]()
Donde ni es la cantidad de niveles del canal i-ésimo que transmite en paralelo; siendo por lo tanto n la cantidad de canales.
![]() es la velocidad de
modulación del i-ésimo canal.
es la velocidad de
modulación del i-ésimo canal.
Si tenemos un solo canal y trabajando con dos niveles como sucede con el sistema binario, la velocidad de transmisión resulta
![]()
La unidad de medida de la velocidad de transmisión es bits/segundo.
Si se tiene un sistema multinivel, se puede incrementar la velocidad de transmisión sin cambiar la velocidad de modulación.
Por ejemplo:
Si ni = 4
![]()
Si ni = 8
![]()
Si tenemos dos bits, las posibles combinaciones serán:
| 0 |
0 |
| 0 |
1 |
| 1 |
0 |
| 1 |
1 |
Si establecemos un nivel para cada combinación obtendremos una señal multinivel
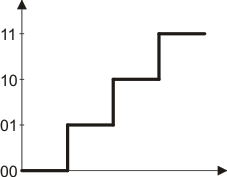
Si aplicamos lo anterior a una secuencia binaria la señal que se transmite tendrá la siguiente forma
Secuencia binaria: 101101001001
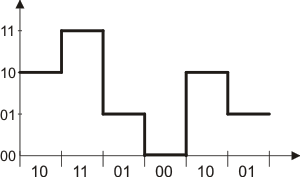
La señal anterior, si bien posee la misma velocidad de modulación que una señal binaria tiene mayor velocidad de transmisión puesto que cada nivel significa la transmisión de 2 bits (dibit).
El concepto de velocidad de modulación se emplea en transmisiones sincrónicas, puesto que en transmisiones asincrónicas carece de sentido ya que no se tiene en cuenta la duración de los bits de arranque y parada.
Velocidad de transferencia de datos
Está dad por la cantidad media de bits que se transmiten entre dos sistemas de datos.

Velocidad real de transferencia de datos
Se denomina así a la cantidad de bits transmitidos en la unidad de tiempo, con la condición que el receptor los considere válidos.
VT > VTransf > VR.Transf
Relación entre el ancho de banda y la velocidad de transmisión
Si se tiene un sistema de comunicaciones a través del cual se transmiten datos binarios, señal cuadrada, y considerando que la frecuencia de dicha señal es de 1 MHz.
De acuerdo al desarrollo de Fourier, por ser la señal cuadrada, solo tendremos armónicas impares y si aceptamos una deformación que permita despreciar a las señales más allá de la 5ª armónica, el ancho de banda necesario para transmitir dicha señal será:
BW = 5f – f = 4f
BW = 5MHz – 1MHz = 4MHz
Ahora bien, si consideramos que a dicha frecuencia estamos transmitiendo ceros y unos, el periodo resultara t = 1 ms, razón por la cual el tiempo de duración de cada bit será 0,5ms y ello implica una velocidad de modulación de 2MBaudios. Si consideramos que se trata de un solo canal y por ser la señal cuadrada tenemos 2 niveles, resulta que la velocidad de transmisión y la velocidad de modulación coinciden numéricamente, resultando la velocidad de transmisión VT = 2Mbits/seg.
Si ahora consideramos tener una señal cuya frecuencia es de 2MHz y aceptamos una distorsión, al igual que en e caso anterior, que permita despreciar a las señales más allá de la 5ª armónica, el ancho de banda resultará
f = 2MHz
BW = 5 2MHz – 2MHz =10 MHz – 2 MHz = 8MHz
En este caso la duración de cada bit es de 0,25 ms, por lo tanto, siguiendo el mismo razonamiento del caso anterior, la velocidad de transferencia resultara de 4Mbits/seg.
Si en un tercer análisis consideramos que la frecuencia de la señal es de 2MHz pero aceptamos una distorsión en la cual se desprecian las señales cuya frecuencia esté más alla de la tercera armónica, el ancho de banda resultara
f = 2MHz
BW = 3 2MHz – 2 MHz = 4MHz
y para la frecuencia dada la velocidad de transmisión es, igual que en el caso anterior, de 4 Mbits/seg.
Del análisis anterior podemos obtener las siguientes conclusiones
- Para transmitir una señal sin deformación se requiere un ancho de banda infinito.
- Todo medio de transmisión disminuye el ancho de banda, razón por la cual todas las señales sufren alguna deformación.
- Cuanto mayor es el ancho de banda mayor es la velocidad de transmisión que puede obtenerse.
- Cuanto mayor es la frecuencia de la señal, mayor es la velocidad de transmisión puesto que cada bit tiene un menor tiempo de duración y ello hace que sea posible enviar mayor cantidad de bits en el mismo tiempo.
Capacidad de un canal
Nyquist determinó que la máxima velocidad alcanzable para un ancho de banda dado es dos veces dicho ancho de banda si no existe ruido.
Si se tienen señales de más de dos niveles, es decir que cada elemento de las señales representa más de un bit, la fórmula de Nyquist resulta
C = 2 BW log2M
donde M es la cantidad de niveles.
Si existe ruido, la velocidad de transmisión debe disminuir pues se corre el riesgo de aumentar la taza de errores ya que mayor cantidad de bits pueden verse afectados en el mismo tiempo.
Solo es posible incrementar la velocidad de transmisión por medio de una transmisión multinivel.
Capacidad de un canal con ruido
Teniendo en cuenta que el ruido es un parámetro fundamental y que el mismo se evalúa en potencia
![]()
Shannon estableció que la capacidad de un canal de comunicaciones esta dada por la siguiente expresión
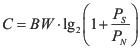
La expresión de Shannon indica el máximo límite teórico que puede obtenerse y a dicha capacidad se la denomina capacidad libre. En forma práctica la capacidad de un canal es siempre menor que la capacidad libre.