Compton inverso y la reflexión interna total

Pico Jiménez Heber Gabriel
Calle 13 No. 10-40 Cereté, Córdoba, Colombia.
heberpico@telecom.com.co

Resumen

Precisamente en este trabajo, partiendo de las conclusiones duales del efecto Compton, fotoeléctrico y Compton Inverso, se logra explicar tras ellas cómo ocurre el fenómeno de la reflexión interna total en la fibra óptica. Este trabajo entonces constituye una prueba adicional de las conclusiones en el efecto Compton. Para poder conservar la energía, un rayo de luz que viaje exitoso cambiando constantemente su dirección en una fibra óptica, es necesario que acontezcan y se repitan las veces requeridas dos Compton inversos simultáneos y contrarios en la frontera que separa los medios de dicha fibra, precisamente ocurren sobre dos electrones contrarios, vecinos de igual energía de enlace pero que se mueven en direcciones diferentes, en uno de ellos pasaría algo parecido a lo que se cree sucede en la emisión de rayos X de supernova, quásares y otros objetos astrofísicos de altas energías. Se demuestra que la ley de Snell es una relación de senos y se consigue la siguiente ecuación que relaciona  a Compton con Snell. La importancia que tiene esta primera ecuación radica en que, identificando los medios por su ángulo Compton, es fácil concretar con la ecuación vecina, la energía que se gasta en determinado choque el fotón de luz, cuestión de importancia en los convertidores de luz a energía en la fibra óptica, asunto que no es posible hacerla con la tradicional ecuación de Snell. Partiendo de la velocidad de la luz en el medio, se calcula el ángulo θ de Compton.

Desarrollo del Tema    

Una teoría física parece demasiado significativa si, además de explicar los fenómenos físicos para la que ha sido construida, puede también explicar otros fenómenos fuera de su dominio original.

Si la ley de Snell se puede derivar a partir del Principio de Fermat, que indica que la trayectoria de la luz es aquella en la que los rayos necesitan menos tiempo para ir de un punto a otro. En el vacio por carencia de puntos y sin ocurrir colisiones, la luz describe indiscutiblemente una trayectoria rectilínea de un solo segmento, describiendo ángulos de cero grados. Pues a medida que en ese mismo espacio se multiplica e incrementa la presencia de puntos o en otras palabras, aumenta la densidad del medio en que se propaga la luz, ella pues va haciendo choques Compton en cada punto y cumpliría dispersiones de punto en punto, recorriendo así cortos trayectos rectos y oblicuos a la velocidad de la luz, cada vez más angulados a partir de cero grados, además después de cada colisión resultará un rayo con menos energía y menos masa cinética, dependiendo todo pues de la densidad del medio, describiendo entonces una trayectoria en zig-zag con ángulos teta de inclinación de los de Compton cada vez mayores a medida que aumenta la densidad, pero constantes del medio respectivo, utilizando en definitiva mayores tiempos para recorrer idénticos espacios, sería un ángulo de incidencia interna cuyo coseno es igual al inverso del índice de refracción identificado del medio en que se desplaza la luz. El coseno de ese ángulo constante interno, ángulo de colisión interna característica de cada medio de propagación es igual, al inverso del preciso índice de refracción de dicha sustancia, este ángulo que llamaremos así, ángulo de colisión interna de naturaleza íntima de esa sustancia, es un ángulo del rayo con respecto a la trayectoria definitiva en que viaja la luz.

Miremos la siguiente tabla, donde están ordenados ascendentemente los índices de refracción, que se incrementan en el mismo sentido que lo hace el ángulo θ, también se nota la relación inversa y como decrece el valor del ángulo critico de los diferentes medios estudiados, claro con respecto al vacío como único medio del rayo incidente del estudio.

Medio	Índice de Refracción	Ángulo Teta	Ángulo Teta medio	Ángulo Noventa menos Teta	Ángulo Critico**
Vacío	1	0	0	90
Aire seco*	1,00029	2,75939679	1,379638395	88,62030161	88,62
Hielo	1,31	80,47759625	40,23879813	49,76120187	49,76
Agua(20ºC)	1,33	82,49306674	41,24653337	48,75346663	48,75
Etanol	1,36	85,33535099	42,6676755	47,33207451	47,33
Acetona	1,36	85,33535099	42,6676755	47,33207451	47,33
Solución Azúcar 30%	1,38	87,1229669	43,56148345	46,43871552	46,43
Cuarzo	1,46	93,53955842	46,76977921	43,23022079	43,23
Glicerina	1,473	94,48659758	47,24329879	42,75670121	42,75
Vidrio Crown	1,52	97,72037917	48,86048959	41,13951041	41,14
Solución Azúcar 80%	1,52	97,72037917	48,86048959	41,13951041	41,14
Vidrio Flint	1,65	105,3835981	52,69479903	37,30520097	37,31
Zafiro	1.77	111,1933406	55,5936703	34,4003297	34,4
Trisulfuro de As.	2,04	121,2930599	60,64652995	29,35347005	29,35
Diamante	2,417	131,1205123	65,56025613	24,43974387	24,44

*Condiciones normales de presión y temperatura

**Angulo Crítico con respecto al vacío.

Cuando un haz de luz que se propaga por un medio que tiene determinado índice de refracción n₁ , índice que es equivalente al inverso del coseno de θ/2, ángulo q de dispersión de Compton, que es el llamado ángulo de desviación interna que tiene toda sustancia. Cuando aumenta el índice de refracción de una sustancia, aumenta también el ángulo de colisión interna de la misma manera como lo dice la siguiente relación.

Si ingresa ese rayo a otro medio distinto, pero de menor índice de refracción n₂, le queda más fácil establecer los efectos Compton Inversos configuradores de la reflexión interna total en el primer medio.

Para hallar el ángulo critico de incidencia desde el cual configuraríamos la reflexión interna total, partimos de la siguiente ecuación.

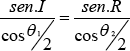
Quiere esto decir que el ángulo limite entre dos medios, lo tienen implícito la relación de los ángulos de incidencia interna de cada medio, en una relación del medio incidente sobre el medio reflector.

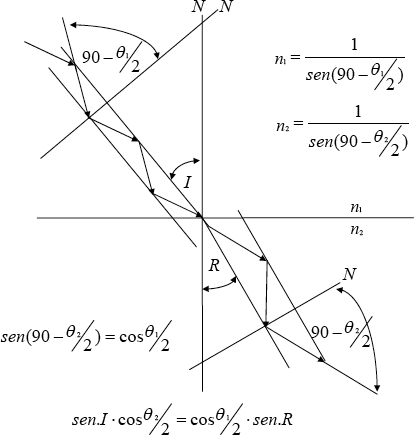
Considerando que el electrón tiene la forma de una sólida partícula esférica, la recta normal a esa respectiva superficie sería una perpendicular que limita dos ángulos iguales que serían, por un lado estaría el ángulo de incidencia y por el otro el ángulo de reflexión, a la vez tal recta debe pasar por el centro esférico del electrón. Además siendo esférica su forma, la dirección de dicha normal cambiaría orientación relativa de acuerdo a la orientación y ubicación de los ángulos referidos que la construyen.

La simetría de la ley de Snell alrededor de una superficie de separación, implica que las trayectorias de los rayos de luz son reversibles. Es decir, si un rayo incide sobre una superficie de separación con un ángulo de incidencia I, se refracta sobre el segundo medio con un ángulo de refracción R entonces, suponiendo un rayo incidente en la dirección opuesta desde el medio 2 con un ángulo de incidencia R, se refracta sobre el medio 1 con un ángulo I. La simetría de la ley de Snell parece seguir la ley de la simetría similar que guarda el Compton Inverso alrededor de la recta normal a la superficie de separación de los medios.

Todo parece indicar que cuando uno estudia al rayo dispersado del efecto Compton, representa el preciso rayo de reflexión en Snell. Igual podemos decir de la refracción representada en Compton por el electrón.

Entonces podemos decir que la diferencia en los medios indicada por Snell con el índice de refracción, en el estudio de Compton está representado por la energía de enlace del electrón chocado.

Si el rayo incidente cuenta con mayor energía que la respectiva energía de enlace del electrón chocado, entonces ocurre el efecto Compton siendo θ + φ = 90 ilustrado en la figura No.1. Pero si además de tener mayor energía tiene dirección y sentido especial con el ángulo θ = 90 y φ = 0, entonces se configura es el efecto fotoeléctrico como se ilustra en la figura No.2. Quedando I = R = 0

Si el rayo incidente tiene menor energía que la respectiva energía de enlace del electrón chocado, como sucede con los rayos de luz o por decirlo de otra manera, si choca el rayo a un electrón de elevada energía de enlace, entonces lo que se configura es el Compton Inverso y entonces θ - φ = 90 como se muestra en la figura No.3.

En los trabajos “Concepción dual del efecto Compton” y “Concepción dual del efecto fotoeléctrico” se deduce ħv₂ = ħv₁cosθ y ħv_te = ħv₁senθ ħv_tecosθ = ħv₂senθ ħv_teħv_te = ħv₂tanθ . En el efecto Compton inverso si choca el rayo ħv₁ contra un electrón resulta ħv₂. Por simetría alrededor de la recta normal a la superficie del electrón también puede suceder lo contrario es decir: chocaría entonces ħv₂ como rayo incidente y resultaría ħv₁ como rayo dispersado con mayor energía por el Compton inverso como lo ilustra la figura No.5.

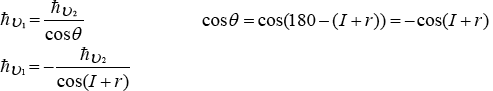
Cuando un haz de luz que se propaga por un medio ingresa a otro distinto, una parte del haz se refleja mientras que la otra sufre una refracción que consiste en el cabio de dirección del haz.

Entonces la reflexión interna total, fenómeno que se cumple en la fibra óptica por llevarse a cabo dos Compton inversos continuos y complementarios en electrones vecinos de iguales energías de enlace pero jamás análogas direcciones. Fenómeno que no quedaría satisfactoriamente explicado por la relación de Snell ya que con ella se llega solo al ángulo límite.

Vale la pena resaltar que la dirección del electrón se acerca a la normal si se configura el efecto Compton, pero se aleja de ella en el Compton inverso, lo que da a entender que la disyuntiva es si se establece un Compton común y corriente o si es un Compton inverso, cosa que depende de la energía de enlace en los electrones de superficie de los medios relacionados y el limite lo establece el efecto fotoeléctrico. En la reflexión interna total, hay una transferencia continua y aleatoria de masa cinética entre electrones vecinos.

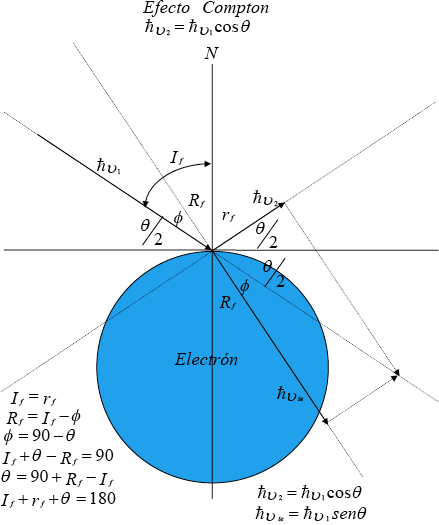
Figura Nº 1

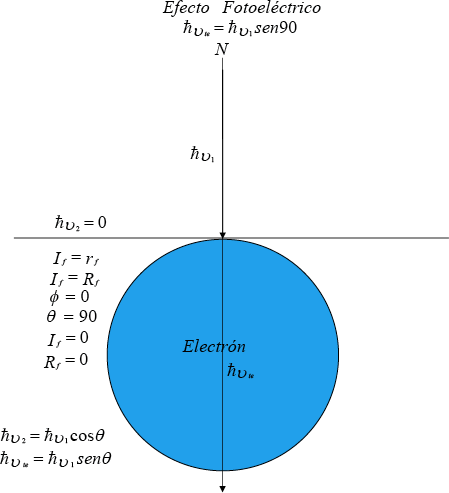
Figura Nº 2

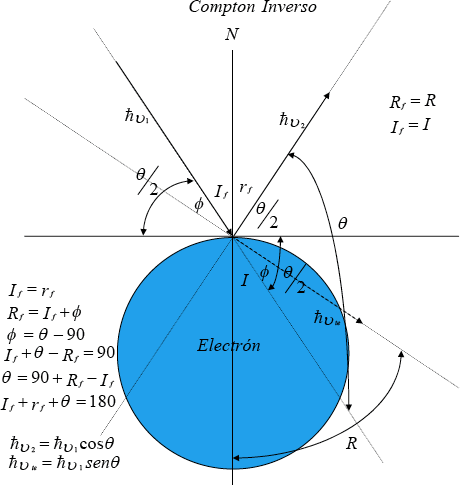
Figura Nº 3

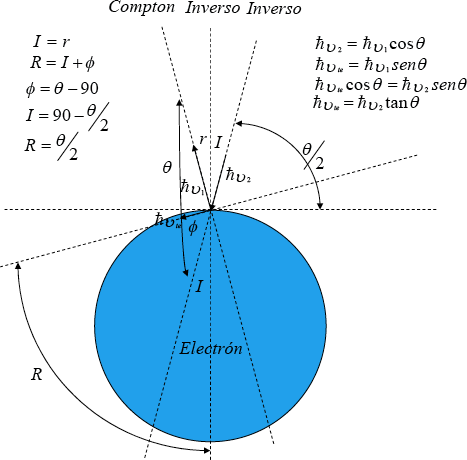
Figura Nº 4

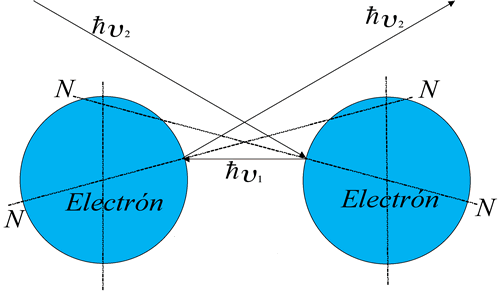
Figura Nº 5

ħ  = Constante de Planck

ħv₁ = Energía cinética del rayo incidente.

ħv₂ = Energía cinética del rayo reflejado.

ħv_te = Energía cinética del electrón chocado.

I = Angulo de incidencia con la normal.

R = Angulo de refracción con la normal.

r = Angulo de reflexión con la normal.

θ = Angulo de dispersión en Compton.

Angulo entre rayo incidente y electrón chocado.