Del punto de vista histórico, los conceptos de calor y temperatura están a la base de la Termodinámica, pero aquí daremos una presentación algo diferente. En nuestro tratamiento, el calor tiene un rol subordinado y es una magnitud que se deriva de otras debido a las dificultades lógicas que aparecen si intentamos definirlo a priori. La temperatura, en cambio, sigue jugando un rol primario. Es una propiedad esencial en nuestra materia Física II. Su determinación cuantitativa (medida) se realiza con instrumentos llamados termómetros. La Ley Cero de la Termodinámica postula que es posible medir la temperatura, es decir, que la temperatura es una propiedad.
Es un hecho conocido que varias propiedades físicas de los cuerpos cambian con la temperatura.
Por ejemplo, los gases, líquidos y sólidos se expanden y se contraen a medida que su temperatura aumenta o disminuye, si la presión se mantiene constante. Las variaciones de temperatura producen también cambios de otras propiedades, tales como la resistividad eléctrica de los materiales o la fuerza electromotriz entre materiales disímiles, etc. Dichas propiedades, que se encuentran entre aquellas que se aprovechan para diseñar termómetros, se denominan propiedades termométricas.
Equilibrio térmico
La temperatura T es aquella propiedad que determina la capacidad de un sistema para intercambiar calor. Su unidad es el kelvin (K).
Suponemos dos subsistemas A y B cerrados de paredes adiabáticas, definidos respectivamente por sus variables de equilibrio x1A, y1A, x1B, y1B, ambos independientes entre sí.
Si se sustituye la pared adiabática que los separa por otra diatérmica se observa experimentalmente que se rompe el equilibrio existente y cada sistema varía su estado hasta alcanzar estados de un nuevo equilibrio, que llamaremos de equilibrio térmico. Los nuevos valores de las variables de estado que definen dicho equilibrio ya no son, como antes, independientes, sino que están ligados por una relación llamada ecuación del equilibrio térmico.
F(x2A, y2A, x2B, y2B) = 0 [2.01]

Equilibrio térmico
Ley cero
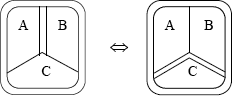
Consideramos ahora tres subsistemas A, B y C, separados dos de ellos, A y B, por una pared adiabática, y C separado de A y B por paredes diatérmicas. Se observa experimentalmente que si, en virtud del equilibrio térmico, A-C y B-C están en equilibrio térmico, también lo están A-B, a pesar de no estar separados por una pared diatérmica, esto bien podría comprobarse permutando el tipo de pared entre los subsistemas A-B-C (ver Figura). Esto equivale a decir que la propiedad "equilibrio térmico" es transitiva, es decir:
Si dos sistemas A y B están en equilibrio térmico cada uno de ellos con un tercero C, los sistemas A y B están en equilibrio térmico entre sí.
Esto constituye el llamado Principio Cero de la Termodinámica, por el cual la existencia del equilibrio térmico entre dos sistemas puede verificarse a través de un sistema intermedio llamado termómetro, sin necesidad de que los dos sistemas estén necesariamente en contacto a través de una pared diatérmica.
Temperatura Empírica
Temperatura empírica es aquella propiedad cuyo valor es el mismo para todos los sistemas que están en equilibrio térmico entre sí.
La formulación del Principio Cero es:
F(xA, yA, xC, yC) = 0
F(xB, yB, xC, yC) = 0
⇔ F(xA, yA, xB, yB) = 0
es decir, el equilibrio térmico entre A y B puede establecerse a través del equilibrio térmico con un sistema intermediario C llamado termómetro.
Despejando de las formulas anteriores, tenemos
xC = ƒA(xA,yA,yC) = ƒB(xB,yB,yC)
Si, para más simplicidad, tomamos como fija la variable yC del sistema termométrico,
Quedará:
xC = ƒA(xA,yA) = ƒB(xB,yB)
[2.02]
La existencia de equilibrio térmico entre dos sistemas (A, B) viene medida por una propiedad común (xC) del sistema termométrico que llamaremos variable termométrica; su valor está indisolublemente ligado a las propiedades físicas del sistema medidor (variable empírica).
La representación gráfica de
xC = ƒA(xA,yA) = ƒB(xB,yB)
[2.03]
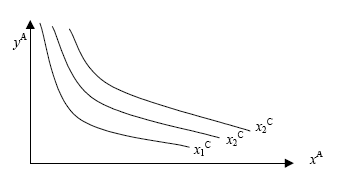
para cada sistema dará lugar a una familia de curvas no intersectantes que son los lugares geométricos del sistema para los que el termómetro señala un mismo valor de la variable termométrica, estas curvas son llamas isotermas:
Isotermas
Se puede establecer una relación simple arbitraria (de tipo lineal, cuadrático, logarítmico, etc.) entre la variable termométrica x y una nueva variable llamada temperatura empírica t del tipo:
t = ax + b o bien t = ax
[2.04]
que permite disponer de una escala más sencilla de valores, llamada escala de temperatura empírica, a través de esta ecuación termométrica. Esta ecuación debe cumplir las siguientes condiciones:
- que sea continua, sin discontinuidades ni puntos angulosos;
- que sea biunívoca, que a cada valor de x corresponda uno sólo de t y viceversa;
- que sea monótona (ordinariamente de derivada positiva) para que sean del mismo signo el crecimiento de t y de x.
La combinación de [2.03] y [2.04] conduce a la expresión:
t = f(x, y)
[2.05]
para un sistema dado, ecuación de estado térmica del sistema, cuya forma depende de la escala de temperatura considerada. No debe pues extrañar que el valor de t sea diferente, para un mismo valor de x e y del sistema, según cuál sea el sistema termométrico utilizado, es decir, el valor de t es empírico.
Los sistemas más usados como termómetros son:
- Los de líquido cuya propiedad fija es la presión, y variable el volumen o mejor la
longitud del fluido en el tubo (al ser la sección calibrada); - Los de gas que toman como propiedad fija bien la presión o bien el volumen.
- Los termoeléctricos que toma como propiedad la resistencia eléctrica de un material conductor.
- Las termocuplas que toman como propiedad la fem generada en la unión de dos materiales conductores de diferentes características.
Algunos puntos fijos que se han empleado históricamente son: alcohol hirviendo (~80°C), hielo fundiéndose (0 °C), agua hirviendo (100 °C), temperatura del cuerpo humano (37 °C), nieve con sal (–18 °C), etc.
La Ley Cero permite una definición provisional de la temperatura (temperatura empírica), hasta que el Segundo Principio nos permita formular una definición termodinámica.
Escala de temperaturas del gas ideal
Para cuantificar el valor de la temperatura empírica es necesario establecer una escala de temperaturas. La escala Celsius emplea dos puntos fijos (los puntos de fusión y de ebullición del agua pura, a 1 atm de presión), a los que da arbitrariamente los valores numéricos de 0 y 100 °C.
Sin embargo, cualquier magnitud física debe requerir de un solo punto fijo para su definición. Esto se consigue con el termómetro de gas a presión constante o a volumen constante. Explicaremos el de presión constante por su mayor simplicidad.
El termómetro se introduce en un sistema cuya temperatura se desea medir. En el termómetro de gas a presión constante la propiedad termométrica es el volumen ocupado por el gas, manteniendo constante la presión de dicho gas. Gay-Lussac realizó medidas del volumen ocupado por el gas cuando el sistema analizado era hielo fundente (t = 0°C), y cuando el sistema era agua hirviendo (t = 100 °C). Comprobó que, con independencia de la cantidad de gas introducida, la relación entre ambos volúmenes variaba poco según qué gas introdujera en el termómetro:
• N2: V100 = 1,3749 V0
• Aire: V100 = 1,375 V0
• O: V100 = 1,3748 V0
• H2: V100 = 1,3752 V0
• Gas cualquiera (media): V100 = 1,375 V0
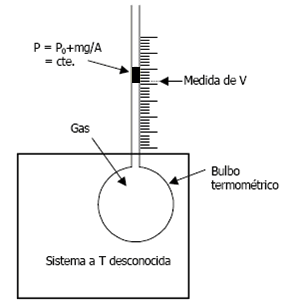
Termómetro de gas a presión constante. La variable termométrica (es decir, la propiedad que varía con la temperatura) es el volumen ocupado por el gas. La presión del gas (el peso del pistón más la atmósfera) se mantiene constante.
Es decir, el coeficiente de expansión térmica de los gases (incremento relativo de volumen por unidad de aumento de temperatura) es:
![]()
[2.06]
Se comprobó que la semejanza entre los gases era tanto mayor cuanto:
a) el gas es más “permanente”; gas a una presión y temperatura muy alejadas de su estado líquido.
b) la presión del gas es menor.
De este modo, se puede hacer una abstracción denominada gas ideal, que sólo necesita un punto fijo de temperatura conocida (V0) para la medida de cualquier otra temperatura:
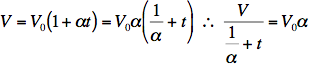
[2.07]
El punto fijo que se toma no es el punto de fusión del agua, sino el punto triple del agua (0,01 °C y 0,611 kPa), en el que coexisten en equilibrio hielo, agua líquida y vapor. En ese estado, el valor experimental más exacto por el momento es α = 0,0036609 °C–1. Si creamos una escala de temperaturas θ = 1/α + t, la medida del volumen será simplemente proporcional a la temperatura del sistema en esa escala:
![]()
La escala θ es una medida independiente de la sustancia, directamente proporcional a la medida del termómetro, y con un cero físico. Es la escala de temperaturas del gas ideal; Esta escala coincide con la temperatura absoluta (Kelvin). Al punto de referencia (punto triple del agua) se le da un valor de la temperatura de 273,16, con unidades de Kelvin (K).
El termómetro es válido solamente para gases a muy bajas presiones; sólo entonces, el termómetro resulta ser independiente del gas contenido en el bulbo, y por tanto válido para establecer una escala universal (empírica) de temperaturas.
![]()
[2.08]
También puede medirse la temperatura empírica con un termómetro de gas a volumen constante; se mide la presión del gas manteniendo constante el volumen que ocupa. El razonamiento es totalmente paralelo al del termómetro de gas a presión constante.
Otras escalas de temperaturas
- Celsius: t [°C] = T [K] – 273,15; Δt [°C] = ΔT [K]
- Fahrenheit: t [°F] = t [°C]*1,8 + 32; Δt [°F] = Δt [°C]*1,8
- Rankine: T [°R] = T [K]*1,8 = t [°F] + 459,67; ΔT [°R] = ΔT [K]*1,8 = Δt [°F]