The space-time is curved environment to the mass of neutral or charged electrically
Por Heber Gabriel Pico Jiménez MD
Resumen
Hasta ahora hemos descrito de como el espacio-tiempo se curva entorno al observador pero, en este artículo se quiere describir sin contradicción y en un mismo escenario, de cómo el espacio-tiempo también se curva entorno a la masa si es neutra o si la masa tiene carga eléctrica. Para esto es que hemos usado en ambas situaciones tanto a la velocidad relativa como a la aceleración gravitacional relativa de un observador con respecto a la masa neutra o cargada de una partícula observada cualquiera, la velocidad relativa y la aceleración gravitacional en ambas situaciones tienen la misma dirección por lo tanto en ese sentido, se les puede aplicar la relación de Newton que define a la velocidad relativa cuando tiene la misma dirección de la gravedad en un movimiento rectilíneo uniformemente acelerado. Este artículo consigue así a la ecuación de la gravedad cuántica que es la siguiente:
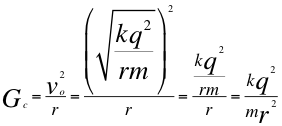
Donde Gc es la gravedad cuántica, voes la velocidad orbital cuántica, k es la constante de Coulomb, q es la carga eléctrica, m es la masa de la partícula cargada, r es el radio desde el centro de la partícula hasta el observador y m es la masa de la partícula observada.
Palabras claves: Gravedad Cuántica, Masa nuclear, Radio atómico.
Abstract
So far we have described of as space-time is curved environment to the observer, but in this article is to describe without contradiction and at one stage, of how space-time also curved environment to the dough if it is neutral or mass has electric charge. For this is that we have used in both situations both at the relative speed as to the gravitational acceleration on an observer with respect to the neutral or charged with one observed particle any mass, relative velocity and the acceleration of gravity in both situations have the same address therefore in this regard, the relationship of Newton that defines the relative velocity when it has the same direction of gravity can be applied to them in a uniformly accelerated rectilinear motion. This article gets so into the equation of quantum gravity.
Keywords: Quantum Gravity, nuclear mass, Atomic RADIUS.
1. Introducción
Este artículo se basa sobre todo en las últimas publicaciones denominadas Energía del Vacío, la Energía Cinética, el Agujero Negro de Kerr-Newman-Pico. También introduce a este trabajo la “configuración electrónica de la gravedad cuántica”. Sirve como introducción el trabajo del Radio del protón es el radio de un Leptón. También hace parte de la introducción de este trabajo el anterior artículo de los Números cuánticos en la gravedad cuántica. También hace parte de introducción el trabajo del espacio tiempo se curva entorno al observador. Hay otros trabajos como velocidad de escape de una partícula no neutra, la velocidad de escape es la velocidad del observador. La velocidad de escape tiene dos valores, dos direcciones y dos observadores distintos.
Este trabajo quiere sostener que la gravedad en sí es la conservación de ángulo en la siguiente ecuación:
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador.
2. Desarrollo del Tema.
La velocidad resultante va cambiando su ángulo debido a los efectos gravitacionales.
El espacio-tiempo del observador entonces no es lineal sino que lo siente curvo en cuatro dimensiones de la siguiente manera:
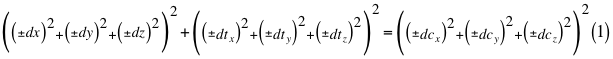
Donde dx es el diferencial espacial de una de las tres coordenadas cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dy y dz son los otros dos diferenciales espaciales restantes de todas las tres coordenadas cartesianas espaciales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial del tiempo y dc es el diferencial espacial de la luz en el vacío.
![]()
Donde dtx es el diferencial del tiempo de una de las tres coordenadas temporales cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dty y dtz son los otros dos diferenciales temporales restantes de las tres coordenadas cartesianas temporales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial resultante del tiempo.
![]()
Donde dcx es el diferencial espacial de la velocidad de la luz en una de las tres coordenadas temporales cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dcy y dcz son los otros dos diferenciales espaciales restantes de las tres coordenadas cartesianas espaciales de la luz quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dc es la diferencial resultante de la velocidad de la luz.
Reemplazando 1a y 1b en la primera ecuación número uno (1) nos queda lo siguiente:
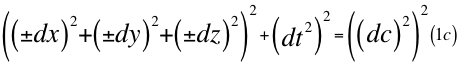
Donde dx es el diferencial de una de las tres coordenadas cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dy y dz son los otros dos diferenciales restantes de las tres coordenadas cartesianas espaciales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial del tiempo y dc es el diferencial espacial de la luz en el vacío.
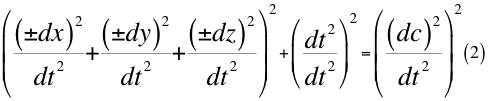
Donde dx es el diferencial de una de las tres coordenadas cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dy y dz son los otros dos diferenciales restantes de las tres coordenadas cartesianas espaciales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial del tiempo y dc es el diferencial espacial de la luz en el vacío.
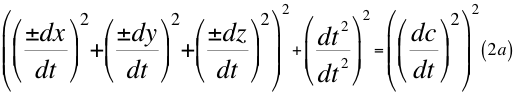
Donde dx es el diferencial de una de las tres coordenadas cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dy y dz son los otros dos diferenciales restantes de las tres coordenadas cartesianas espaciales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial del tiempo y dc es el diferencial espacial de la luz en el vacío.

Donde vx, es una de las tres velocidades que integran el marco de referencia del observador y que está ubicada paralelamente en el mismo eje que pasa tanto por el observador como por la partícula que se observa, vy y vz son las otras dos velocidades del marco de referencia y son las componentes de la velocidad orbital resultante del observador en el referido marco de referencia aplicado y c es la velocidad de la luz en el vacío.
![]()
Donde vx es la velocidad de acercamiento o si es del caso la velocidad de alejamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y vres la velocidad resultante total del observador en ese marco de referencia que es producto de la suma de las tres velocidades cartesianas.
Reemplazamos cuatro (4) en tres (3) y nos queda:
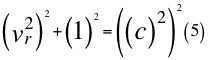
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
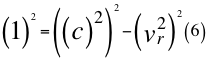
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
![]()
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
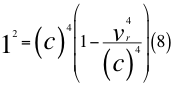
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
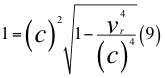
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
Reemplazamos nueve (9) en cinco (5) y nos queda:
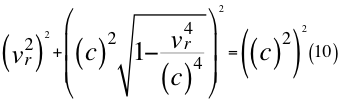
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
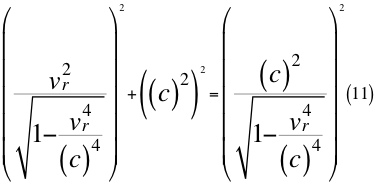
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
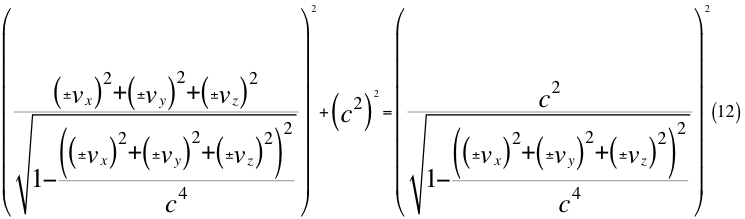
Donde vx es la velocidad de acercamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y c es la velocidad de la luz en el vacío.
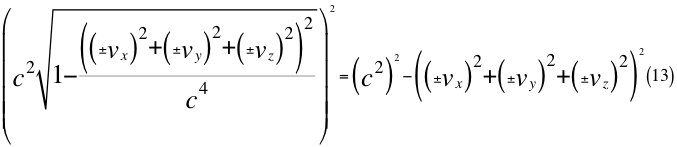
Donde vx es la velocidad de alejamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y c es la velocidad resultante total del observador en ese marco de referencia que es producto de la luz en el vacío.
Los componentes de la velocidad resultante del observador con respecto a una partícula que observa ubicada en uno de sus ejes, a cierta distancia de uno de los ocho marcos de referencia que tiene a su alrededor el observador tanto en la relatividad especial, la relatividad general y en la misma mecánica cuántica:
EL ESPACIO TIEMPO-CURVADO ENTORNO AL OBSERVADOR DE PARTÍCULA ELÉCTRICAMENTE NEUTRA EN LA RELATIVIDAD ESPECIAL
Cuando estas dos ecuaciones anteriores logran chocar con la partícula de masa m que el mismo observa, esta masa se involucra escalarmente en la ecuación multiplicando de la misma manera a toda la ecuación:
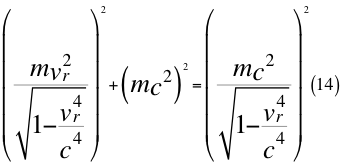
Donde m es la masa invariante de la partícula que se observa, vr es la velocidad resultante total producto de tres coordenadas cartesianas de la velocidad del observador de la partícula y c es la velocidad de la luz en el vacío.
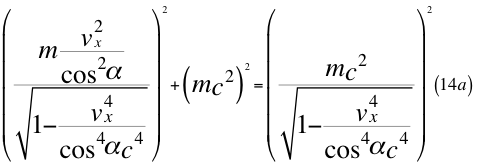
Donde m es la masa invariante de la partícula que se observa, vr es la velocidad resultante total producto de tres coordenadas cartesianas de la velocidad del observador de la partícula y c es la velocidad de la luz en el vacío.
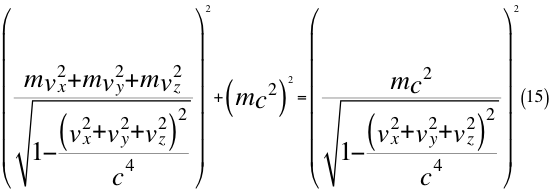
Donde m es la masa invariante de la partícula que se observa, vx es la velocidad de alejamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y c es la velocidad resultante total del observador en ese marco de referencia que es producto de la luz en el vacío.
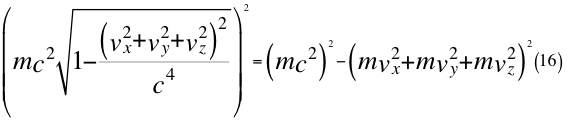
Donde m es la masa invariante de la partícula que se observa, vx es la velocidad de alejamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y c es la velocidad resultante total del observador en ese marco de referencia que es producto de la luz en el vacío.
EL ESPACIO TIEMPO-CURVADO ENTORNO AL OBSERVADOR DE PARTÍCULA ELÉCTRICAMENTE NEUTRA DE LA RELATIVIDAD GENERAL
![]()
Donde vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y voes la velocidad orbital del observador en ese marco de referencia.
Reemplazamos dieciséis a (16a) en doce y trece y nos queda:
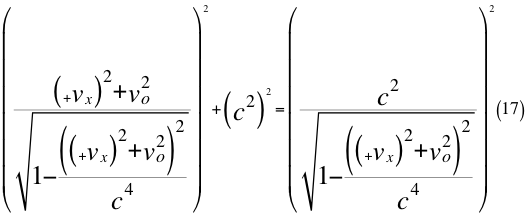
Donde vx es la velocidad de acercamiento a la partícula ubicada en el eje que pasa por la partícula y pasa por el observador, vo es la velocidad orbital resultante del observador y c es la velocidad de la luz en el vacío.
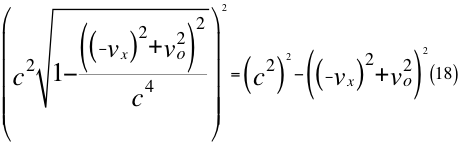
Donde vx es la velocidad de acercamiento a la partícula ubicada en el eje que pasa por la partícula y pasa por el observador, vo es la velocidad orbital resultante del observador y c es la velocidad de la luz en el vacío.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador.

Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador, vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador, G es la constante de gravitación universal, m es la masa invariante de la partícula observada, r es el radio desde el observador hasta el centro de la partícula observada, k es la constante Coulomb, q es la carga eléctrica de la partícula.
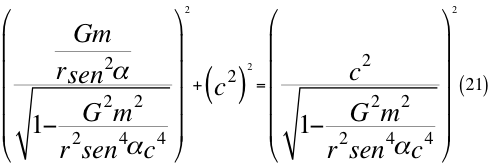
Donde G es la constante gravitacional, m es la masa invariante de la partícula que se observa, r es el radio desde el centro de la partícula hasta el observador, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador y c es la velocidad de la luz en el vacío.
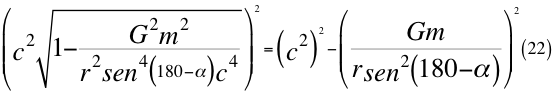
Donde G es la constante gravitacional, m es la masa invariante de la partícula que se observa, r es el radio desde el centro de la partícula hasta el observador, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador y c es la velocidad de la luz en el vacío.
3. Conclusiones.
a)- LA PRIMERA, ÚNICA Y GRAN CONCLUSIÓN de este trabajo es la descripción de como el espacio-tiempo se curva entorno a la masa ya sea neutra o si la masa tiene carga eléctrica, esto se ha hecho utilizando a la velocidad (±vx) deducida por la relación de Newton en el movimiento rectilíneo uniformemente acelerado:
![]()
Donde ±vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador.
La velocidad (±vx) no es constante y va decreciendo a medida que un cuerpo se eleva después de haber sido lanzado, hay que deducirla a partir de la velocidad inicial o velocidad de lanzamiento:
![]()
Donde ±vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, vies la velocidad inicial, g es la aceleración gravitatoria y t es el tiempo transcurrido después de haber sido lanzado.
Reemplazando 22 en 19 nos queda lo siguiente:
![]()
Donde vies la velocidad inicial, g es la aceleración gravitatoria, t es el tiempo transcurrido después de haber sido lanzado, voes la velocidad orbital del observador en ese marco de referencia y vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador.
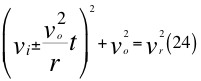
Donde vies la velocidad inicial, voes la velocidad orbital del observador en ese marco de referencia, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento y vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador.
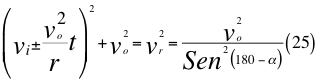
Donde vies la velocidad inicial, voes la velocidad orbital del observador en ese marco de referencia, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
Relacionamos a la velocidad inicial poniéndola como un múltiplo de la velocidad orbital de la siguiente manera
![]()
Donde ±vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, vies la velocidad inicial, g es la aceleración gravitatoria y t es el tiempo transcurrido después de haber sido lanzado.
Reemplazamos 26 en 25 y nos queda lo siguiente:
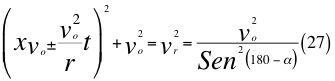
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, voes la velocidad orbital del observador en ese marco de referencia, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
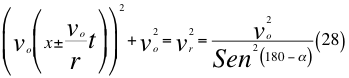
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, voes la velocidad orbital del observador en ese marco de referencia, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
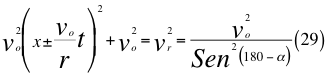
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, voes la velocidad orbital del observador en ese marco de referencia, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
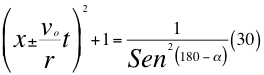
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, voes la velocidad orbital del observador en ese marco de referencia, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador .
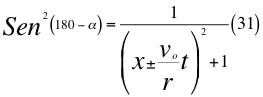
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, voes la velocidad orbital del observador en ese marco de referencia, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
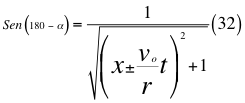
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, voes la velocidad orbital del observador en ese marco de referencia, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
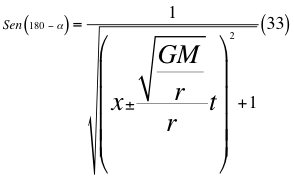
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
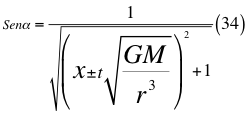
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
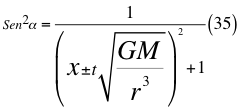
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y α es el ángulo entre la velocidad vx y la velocidad resultante total del observador.
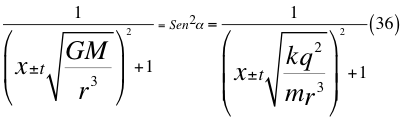
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador, k es la constante de Coulomb, q es la carga eléctrica y m es la masa de la partícula cargada.
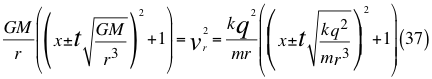
Donde x es un factor de relación entre la velocidad inicial y la velocidad orbital, G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador, k es la constante de Coulomb, q es la carga eléctrica y m es la masa de la partícula cargada.
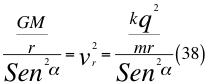
Donde G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador, k es la constante de Coulomb, q es la carga eléctrica y m es la masa de la partícula cargada.
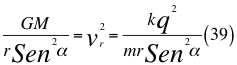
Donde G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador, k es la constante de Coulomb, q es la carga eléctrica y m es la masa de la partícula cargada.
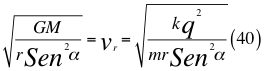
Donde G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador, k es la constante de Coulomb, q es la carga eléctrica y m es la masa de la partícula cargada.
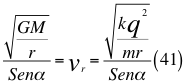
Donde G es la constante gravitacional, M es la masa del cuerpo masivo, t es el tiempo transcurrido después de haber sido lanzado, r es el radio del cuerpo masivo desde donde se hace el lanzamiento, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador, k es la constante de Coulomb, q es la carga eléctrica y m es la masa de la partícula cargada.
![]()
Donde vo y voc es la velocidad en la relatividad general y de la mecánica cuántica, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador, vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador, k es la constante de Coulomb, q es la carga eléctrica y m es la masa de la partícula cargada.
ECUACIÓN DE LA GRAVEDAD CUÁNTICA
La ecuación de la gravedad cuántica, es aquella relación de la gravedad que generan las masas que tienen carga eléctrica:
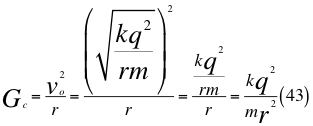
Donde Gc es la gravedad cuántica, voes la velocidad orbital, k es la constante de Coulomb, q es la carga eléctrica, m es la masa de la partícula cargada, r es el radio desde el centro de la partícula hasta el observador.
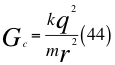
Donde Gc es la gravedad cuántica, voes la velocidad orbital, k es la constante de Coulomb, q es la carga eléctrica, m es la masa de la partícula cargada, r es el radio desde el centro de la partícula hasta el observador.
4- Referencias
REFERENCIAS DEL ARTÍCULO.
[38] El ángulo de la Gravedad.
[37] La velocidad de escape tiene dos valores, dos direcciones y dos observadores distintos.
[36] La velocidad de escape es la velocidad del observador.
[35] Velocidad de escape de una partícula con carga eléctrica no neutra.
[34] Velocidad de escape de una partícula con carga eléctrica no neutra.
[33] El espacio tiempo se curva entorno al observador
[32] El espacio-tiempo se curva entorno al observador
[31] Números cuánticos en la gravedad cuántica.
[30] Números cuánticos en la gravedad cuántica.
[29] Radio del protón es el de un Leptón.
[28] Configuración el electrónica de la gravedad cuántica.
[27] Configuración electrónica de la gravedad cuántica.
[26] Agujero Negro de Kerr-Newman-Pico.
[25] Agujero Negro de Kerr-Newman-Pico.
[24] Energía Cinética
[23] Energía del Vacío
[22] Energía del Vacío
[21] Agujero Negro de Schwarzschild.
[20] Agujero Negro de Schwarzschild.
[19] Velocidad de escape de una singularidad gravitatoria.
[18] Velocidad de escape de una singularidad gravitacional.
[17] Velocidad Orbital del Electrón.
[16] Velocidad Orbital del Electrón
[15] Espacio tiempo curvo de la gravedad cuántica
[14] Dilatación unificada del tiempo
[13] Gravedad Cuántica
[12] Efecto Doppler Relativista.
[11] Energía en Reposo
[10] Onda Gravitacional
[09] Ondas de materia
[08] Ondas gravitacionales de vacío cuántico.
[07] Ondas gravitacionales de vacío cuántico.
[06] Tercer número cuántico
[05] Electron como cuasipartícula
[04] Hibridación del Carbono
[03] tercer número cuántico
[02] Hibridación del carbono.
[01] Electrón Cuasipartícula.
[1] Nueva tabla periódica.
[2] Nueva tabla periódica.
[3] Ciclo del Ozono
[4] Ciclo del Ozono
[5] Barrera Interna de Potencial
[6] Barrera Interna de Potencial
[7] Ácido Fluoroantimónico.
[8] Ácido Fluoroantimónico.
[9] Dióxido de cloro
[10]Dióxido de cloro
[11]Pentafluoruro de Antimonio
[12]Pentafluoruro de Antimonio
[13]Tetróxido de Osmio
[14]Enlaces Hipervalentes
[15]Enlaces en moléculas Hipervalentes
[16]Nueva regla del octeto
[17]Estado fundamental del átomo
[18]Estado fundamental del átomo
[19]Barrera rotacional del etano.
[20]Enlaces de uno y tres electrones.
[21]Enlaces de uno y tres electrones.
[22]Origen de la barrera rotacional del etano
[23]Monóxido de Carbono
[24]Nueva regla fisicoquímica del octeto
[25]Células fotoeléctricas Monografías.
[26]Células Fotoeléctricas textoscientificos.
[27]Semiconductores Monografías.
[28]Semiconductores textoscientificos.
[29]Superconductividad.
[30]Superconductividad.
[31]Alotropía.
[32]Alotropía del Carbono.
[33]Alotropía del Oxígeno.
[34]Ozono.
[35]Diborano
[36]Semiconductores y temperatura.
REFERENCIAS DE LA TEORÍA
[1] Número cuántico magnético.
[2] Ángulo cuántico
[3] Paul Dirac y Nosotros
[4] Numero cuántico Azimutal monografías
[5] Numero cuántico Azimutal textoscientificos
[6] Inflación Cuántica textos científicos.
[7] Números cuánticos textoscientíficos.com.
[8] Inflación Cuántica Monografías
[9] Orbital Atómico
[10] Números Cuánticos.
[11] Átomo de Bohr.
[12] Líneas de Balmer.
[13] Constante Rydberg.
[14] Dilatación gravitacional del tiempo.
[15] Número Cuántico magnético.
[16] Numero Cuántico Azimutal.
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena Rep. De Colombia. Investigador independiente de problemas biofísicos médicos propios de la memoria, el aprendizaje y otros entre ellos la enfermedad de Alzheimer.
Estos trabajos, que lo más probable es que estén desfasados por la poderosa magia secreta que tiene la ignorancia y la ingenuidad, sin embargo, como cualquier representante de la comunidad académica que soy, también han sido debidamente presentados sobretodo este se presentó en Enero 24 del 2016 en la “Academia Colombiana de Ciencias Exactas, Físicas y Naturales” ACCEFYN.