The Escape Velocity has two values, two addresses, and two different observers
Por Heber Gabriel Pico Jiménez MD
Resumen
La velocidad relativa de un cuerpo, sería una velocidad medida por un observador que si se le curva el espacio tiempo a su alrededor, es con respecto al cuerpo que se mueve y no con respecto a la tierra donde está parado debido a que ese observador en reposo, no siente la velocidad orbital del planeta. Esa velocidad relativa del cuerpo para ese observador en reposo, podría llegar a tener cualquier dirección y un valor mínimo lo suficientemente grande como para escapar de la tierra. Pero qué pasa si esa misma velocidad relativa del cuerpo la mide es otro observador global cuyo espacio-tiempo se curva en su entorno es con respecto al planeta que se le mueve, pues el valor de esa misma velocidad del cuerpo se ubicará en el espacio-tiempo curvo del planeta y lo hará, con una dirección totalmente perpendicular a la velocidad orbital del respectivo planeta. Es decir que al observador terrenal en reposo, le resultaría una velocidad de escape que tiene un valor y una dirección totalmente distintas al valor y la dirección que tendría la velocidad de escape del observador en el espacio-tiempo curvo. El valor de la velocidad de escape en la superficie de la Tierra con cualquier dirección para el observador terrenal es igual a 7,919 km/sg mientras que el valor de la velocidad de escape, para el observador del espacio-tiempo curvo de la Tierra, tiene siempre una dirección definida y un valor de es 11,2 km/sg.
Palabras claves: Gravedad Cuántica, Masa nuclear, Radio atómico.
Abstract
The relative speed of a body, would be a speed measured by an observer that if curves you space time to his around, is about the body that moves and not with respect to the Earth where stands since the observer at rest, do not feel the orbital velocity of the planet. The relative speed of the body for this observer at rest, could become to have any direction and a large enough minimum value to escape from the land. But if that same relative velocity of the body measured is another global observer whose space-time is curved in its environment is with respect to the planet that moves you, because the value of that same body speed clinches, the curved space-time of the planet and will do so with a completely perpendicular to the orbital velocity of the respective planet. I.e. that the earthly observer at rest, would find an escape velocity that has a value and address completely different to the value and the address that would have, the speed of the observer in curved space-time. The value of the escape velocity at the surface of the Earth with any direction for the terrestrial observer is equal to 7,919 km/sec while the value of the escape velocity, for the curved space-time observer, always has a defined direction and a value is 11.2 km/sec.
Keywords: Quantum gravity, nuclear mass, Atomic RADIUS.
1. Introducción
Este artículo se basa sobre todo en las últimas publicaciones denominadas Energía del Vacío, la Energía Cinética, el Agujero Negro de Kerr-Newman-Pico. También introduce a este trabajo la “configuración electrónica de la gravedad cuántica”. Sirve como introducción el trabajo del Radio del protón es el radio de un Leptón. También hace parte de la introducción de este trabajo el anterior artículo de los Números cuánticos en la gravedad cuántica. También hace parte de introducción el trabajo del espacio tiempo se curva entorno al observador. Hay otros trabajos como velocidad de escape de una partícula no neutra, la velocidad de escape es la velocidad del observador.
2. Desarrollo del Tema.
Comenzamos describiendo al espacio-tiempo como aquella figura matemática que surge de un observador central que a pesar de estar libre de masa y carga eléctrica, su descripción es solo en uno de los ocho marcos de referencias espacio-temporales y simétricos que rodean al respectivo observador, sujeto incorpóreo que estudiaría a una partícula que esté ubicada a su alrededor a cualquier distancia y en uno de los ejes de los respectivos marcos de referencias.
El espacio-tiempo alrededor de un observador, es curvo y en cuatro dimensiones en torno a este.
El espacio-tiempo del observador entonces no es lineal sino que lo siente curvo en cuatro dimensiones de la siguiente manera:
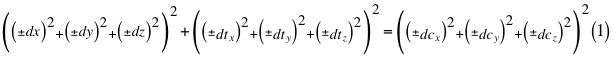
Donde dx es el diferencial espacial de una de las tres coordenadas cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dy y dz son los otros dos diferenciales espaciales restantes de todas las tres coordenadas cartesianas espaciales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial del tiempo y dc es el diferencial espacial de la luz en el vacío.
![]()
Donde dtx es el diferencial del tiempo de una de las tres coordenadas temporales cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dty y dtz son los otros dos diferenciales temporales restantes de las tres coordenadas cartesianas temporales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial resultante del tiempo.
![]()
Donde dcx es el diferencial espacial de la velocidad de la luz en una de las tres coordenadas temporales cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dcy y dcz son los otros dos diferenciales espaciales restantes de las tres coordenadas cartesianas espaciales de la luz quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dc es la diferencial resultante de la velocidad de la luz.
Reemplazando 1ay 1b en la primera ecuación número uno (1) nos queda lo siguiente:
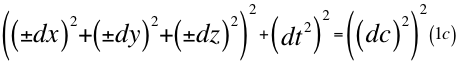
Donde dx es el diferencial de una de las tres coordenadas cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dy y dz son los otros dos diferenciales restantes de las tres coordenadas cartesianas espaciales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial del tiempo y dc es el diferencial espacial de la luz en el vacío.
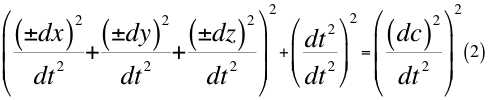
Donde dx es el diferencial de una de las tres coordenadas cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dy y dz son los otros dos diferenciales restantes de las tres coordenadas cartesianas espaciales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial del tiempo y dc es el diferencial espacial de la luz en el vacío.
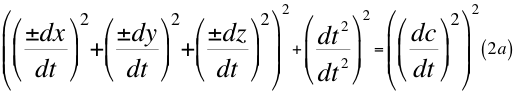
Donde dx es el diferencial de una de las tres coordenadas cartesianas del observador que precisamente está ubicada en el mismo eje radial que pasa también por el centro de la partícula que se observa, dy y dz son los otros dos diferenciales restantes de las tres coordenadas cartesianas espaciales quienes limitan el marco de referencia espacial donde está ubicado el diferencial resultante, dt es la diferencial del tiempo y dc es el diferencial espacial de la luz en el vacío.
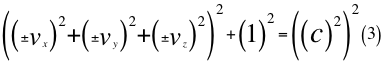
Donde vx, es una de las tres velocidades que integran el marco de referencia del observador y que está ubicada paralelamente en el mismo eje que pasa tanto por el observador como por la partícula que se observa, vy y vz son las otras dos velocidades del marco de referencia y son las componentes de la velocidad orbital resultante del observador en el referido marco de referencia aplicado y c es la velocidad de la luz en el vacío.
![]()
Donde vx es la velocidad de acercamiento o si es del caso la velocidad de alejamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y vres la velocidad resultante total del observador en ese marco de referencia que es producto de la suma de las tres velocidades cartesianas.
Reemplazamos cuatro (4) en tres (3) y nos queda:
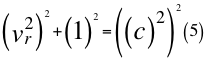
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
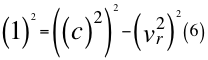
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
![]()
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
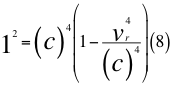
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
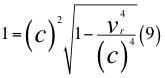
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
Reemplazamos nueve (9) en cinco (5) y nos queda:
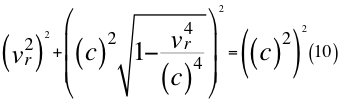
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
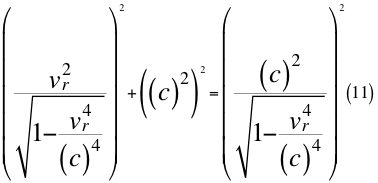
Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador y c es la velocidad de la luz en el vacío.
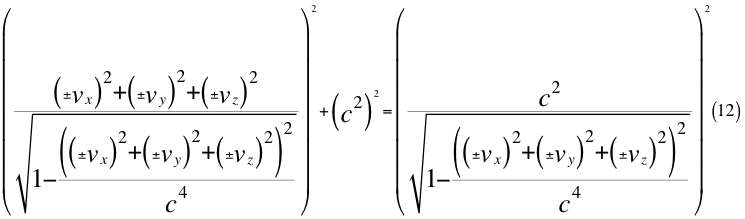
Donde vx es la velocidad de acercamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y c es la velocidad de la luz en el vacío.
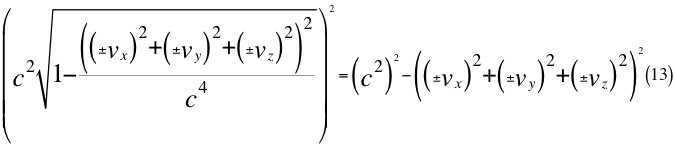
Donde vx es la velocidad de alejamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y c es la velocidad resultante total del observador en ese marco de referencia que es producto de la luz en el vacío.
Los componentes de la velocidad resultante del observador con respecto a una partícula que observa ubicada en uno de sus ejes, a cierta distancia de uno de los ocho marcos de referencia que tiene a su alrededor el observador tanto en la relatividad especial, la relatividad general y en la misma mecánica cuántica:
EL ESPACIO TIEMPO-CURVADO ENTORNO AL OBSERVADOR DE PARTÍCULA ELÉCTRICAMENTE NEUTRA EN LA RELATIVIDAD ESPECIAL
Cuando estas dos ecuaciones anteriores logran chocar con la partícula de masa m que el mismo observa, esta masa se involucra escalarmente en la ecuación multiplicando de la misma manera a toda la ecuación:

Donde m es la masa invariante de la partícula que se observa, vr es la velocidad resultante total producto de tres coordenadas cartesianas de la velocidad del observador de la partícula y c es la velocidad de la luz en el vacío.
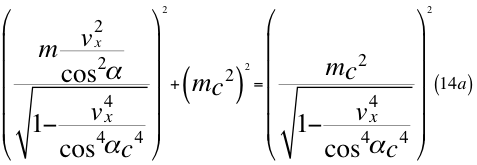
Donde m es la masa invariante de la partícula que se observa, vr es la velocidad resultante total producto de tres coordenadas cartesianas de la velocidad del observador de la partícula y c es la velocidad de la luz en el vacío.
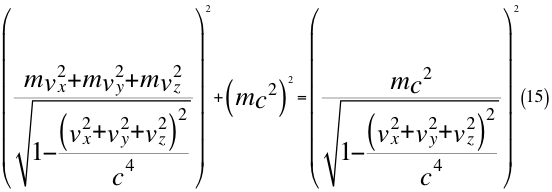
Donde m es la masa invariante de la partícula que se observa, vx es la velocidad de alejamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y c es la velocidad resultante total del observador en ese marco de referencia que es producto de la luz en el vacío.
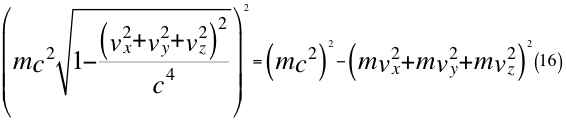
Donde m es la masa invariante de la partícula que se observa, vx es la velocidad de alejamiento ubicada siempre en el eje que une al observador con la partícula que se observa, vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y c es la velocidad resultante total del observador en ese marco de referencia que es producto de la luz en el vacío.
EL ESPACIO TIEMPO-CURVADO ENTORNO AL OBSERVADOR DE PARTÍCULA ELÉCTRICAMENTE NEUTRA DE LA RELATIVIDAD GENERAL
![]()
Donde vy es una de las dos velocidades perpendiculares que componen a la velocidad orbital resultante del observador, vz es la otra velocidad ortogonal componente también de la velocidad orbital resultante del observador y voes la velocidad orbital del observador en ese marco de referencia.
Reemplazamos dieciséis a (16a) en doce y trece y nos queda:
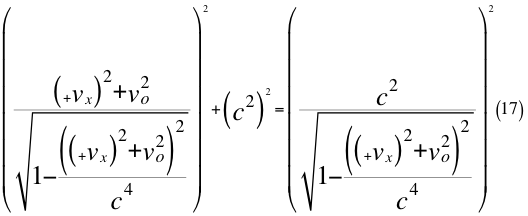
Donde vx es la velocidad de acercamiento a la partícula ubicada en el eje que pasa por la partícula y pasa por el observador, vo es la velocidad orbital resultante del observador y c es la velocidad de la luz en el vacío.
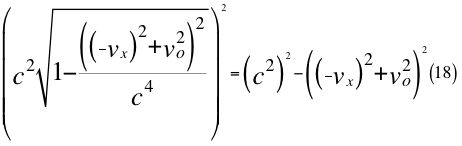
Donde vx es la velocidad de acercamiento a la partícula ubicada en el eje que pasa por la partícula y pasa por el observador, vo es la velocidad orbital resultante del observador y c es la velocidad de la luz en el vacío.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador.

Donde vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador, vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador, G es la constante de gravitación universal, m es la masa invariante de la partícula observada, r es el radio desde el observador hasta el centro de la partícula observada, k es la constante Coulomb, q es la carga eléctrica de la partícula.
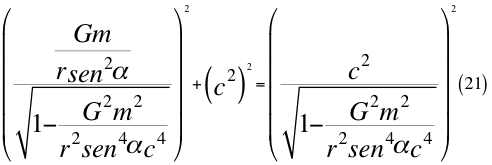
Donde G es la constante gravitacional, m es la masa invariante de la partícula que se observa, r es el radio desde el centro de la partícula hasta el observador, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador y c es la velocidad de la luz en el vacío.
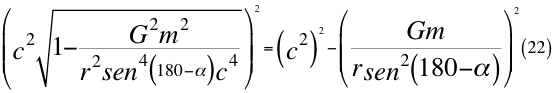
Donde G es la constante gravitacional, m es la masa invariante de la partícula que se observa, r es el radio desde el centro de la partícula hasta el observador, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador y c es la velocidad de la luz en el vacío.
3. Conclusiones.
a)- LA PRIMERA Y ÚNICA GRAN CONCLUSIÓN de este trabajo es la ecuación de donde se deduce la fórmula de la velocidad de escape:
OBSERVADOR TERRENAL
Esta ecuación número 19 en el observador terrenal es con respecto a la partícula que se mueve y no con respecto al planeta.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y vr es la velocidad resultante total del observador en ese marco de referencia producto de las tres velocidades cartesianas del observador.
En esta anterior ecuación, la velocidad orbital de la partícula que se observa desde la tierra es casi cero y si la velocidad resultante es la velocidad de escape, queda lo siguiente:
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y ve es la velocidad terrenal de escape.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa y ve es la velocidad terrenal de escape.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa y ve es la velocidad terrenal de escape.
OBSERVADOR GLOBAL
Esta ecuación número 19 en el observador global es con respecto a la Tierra que se mueve con respecto al observador.
En esta anterior ecuación, la velocidad orbital que se considera es la del planeta tierra y si la velocidad resultante es la velocidad de escape, queda lo siguiente:
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y ve es la velocidad global de escape.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y ve es la velocidad global de escape.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y ve es la velocidad global de escape.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y ve es la velocidad global de escape.
![]()
Donde vx es la velocidad de alejamiento o acercamiento ubicado siempre en el eje que une al observador con la partícula que se observa, voes la velocidad orbital del observador en ese marco de referencia y ve es la velocidad global de escape.
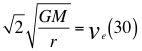
Donde G es la constante gravitacional, M es la masa invariante de la partícula que se observa, r es el radio desde el centro de la partícula hasta el observador y ve es la velocidad global de escape.
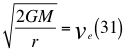
Donde G es la constante gravitacional, M es la masa invariante de la partícula que se observa, r es el radio desde el centro de la partícula hasta el observador y ve es la velocidad global de escape.
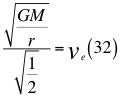
Donde G es la constante gravitacional, M es la masa invariante de la partícula que se observa, r es el radio desde el centro de la partícula hasta el observador y ve es la velocidad global de escape.
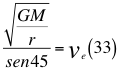
Donde G es la constante gravitacional, M es la masa invariante de la partícula que se observa, r es el radio desde el centro de la partícula hasta el observador y ve es la velocidad global de escape.
![]()
Donde voes la velocidad orbital del observador en ese marco de referencia, α es el ángulo entre la velocidad vx y la velocidad resultante total del observador y ve es la velocidad global de escape.
VELOCIDAD TERRENAL DE ESCAPE
![]()
Donde ve es la velocidad terrenal de escape.
VELOCIDAD GLOBAL DE ESCAPE
![]()
Donde ve es la velocidad global de escape.
4- Referencias
REFERENCIAS DEL ARTÍCULO.
[36] La velocidad de escape es la velocidad del observador.
[35] Velocidad de escape de una partícula con carga eléctrica no neutra.
[34] Velocidad de escape de una partícula con carga eléctrica no neutra.
[33] El espacio tiempo se curva entorno al observador
[32] El espacio-tiempo se curva entorno al observador
[31] Números cuánticos en la gravedad cuántica.
[30] Números cuánticos en la gravedad cuántica.
[29] Radio del protón es el de un Leptón.
[28] Configuración el electrónica de la gravedad cuántica.
[27] Configuración electrónica de la gravedad cuántica.
[26] Agujero Negro de Kerr-Newman-Pico.
[25] Agujero Negro de Kerr-Newman-Pico.
[24] Energía Cinética
[23] Energía del Vacío
[22] Energía del Vacío
[21] Agujero Negro de Schwarzschild.
[20] Agujero Negro de Schwarzschild.
[19] Velocidad de escape de una singularidad gravitatoria.
[18] Velocidad de escape de una singularidad gravitacional.
[17] Velocidad Orbital del Electrón.
[16] Velocidad Orbital del Electrón
[15] Espacio tiempo curvo de la gravedad cuántica
[14] Dilatación unificada del tiempo
[13] Gravedad Cuántica
[12] Efecto Doppler Relativista.
[11] Energía en Reposo
[10] Onda Gravitacional
[09] Ondas de materia
[08] Ondas gravitacionales de vacío cuántico.
[07] Ondas gravitacionales de vacío cuántico.
[06] Tercer número cuántico
[05] Electron como cuasipartícula
[04] Hibridación del Carbono
[03] tercer número cuántico
[02] Hibridación del carbono.
[01] Electrón Cuasipartícula.
[1] Nueva tabla periódica.
[2] Nueva tabla periódica.
[3] Ciclo del Ozono
[4] Ciclo del Ozono
[5] Barrera Interna de Potencial
[6] Barrera Interna de Potencial
[7] Ácido Fluoroantimónico.
[8] Ácido Fluoroantimónico.
[9] Dióxido de cloro
[10]Dióxido de cloro
[11]Pentafluoruro de Antimonio
[12]Pentafluoruro de Antimonio
[13]Tetróxido de Osmio
[14]Enlaces Hipervalentes
[15]Enlaces en moléculas Hipervalentes
[16]Nueva regla del octeto
[17]Estado fundamental del átomo
[18]Estado fundamental del átomo
[19]Barrera rotacional del etano.
[20]Enlaces de uno y tres electrones.
[21]Enlaces de uno y tres electrones.
[22]Origen de la barrera rotacional del etano
[23]Monóxido de Carbono
[24]Nueva regla fisicoquímica del octeto
[25]Células fotoeléctricas Monografías.
[26]Células Fotoeléctricas textoscientificos.
[27]Semiconductores Monografías.
[28]Semiconductores textoscientificos.
[29]Superconductividad.
[30]Superconductividad.
[31]Alotropía.
[32]Alotropía del Carbono.
[33]Alotropía del Oxígeno.
[34]Ozono.
[35]Diborano
[36]Semiconductores y temperatura.
REFERENCIAS DE LA TEORÍA
[1] Número cuántico magnético.
[2] Ángulo cuántico
[3] Paul Dirac y Nosotros
[4] Numero cuántico Azimutal monografías
[5] Numero cuántico Azimutal textoscientificos
[6] Inflación Cuántica textos científicos.
[7] Números cuánticos textoscientíficos.com.
[8] Inflación Cuántica Monografías
[9] Orbital Atómico
[10] Números Cuánticos.
[11] Átomo de Bohr.
[12] Líneas de Balmer.
[13] Constante Rydberg.
[14] Dilatación gravitacional del tiempo.
[15] Número Cuántico magnético.
[16] Numero Cuántico Azimutal.
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena Rep. De Colombia. Investigador independiente de problemas biofísicos médicos propios de la memoria, el aprendizaje y otros entre ellos la enfermedad de Alzheimer.
Estos trabajos, que lo más probable es que estén desfasados por la poderosa magia secreta que tiene la ignorancia y la ingenuidad, sin embargo, como cualquier representante de la comunidad académica que soy, también han sido debidamente presentados sobretodo este se presentó en Enero 10 del 2016 en la “Academia Colombiana de Ciencias Exactas, Físicas y Naturales” ACCEFYN.