Función de onda angular: la "forma" de los orbitales atómicos.
La parte angular de la función de onda de un orbital hidrogenoide Ql,ml(θ) Φml(φ) determina la forma de la nube electrónica, y en consecuencia del orbital, así como su orientación en el espacio. Esta función de onda es independiente del número cuántico principal n:
Θl,ml (θ) Φml(φ) = (1/4π)1/2Ψ(θ,φ)
Función de onda angular: valor de Ψ(θ,φ)
l |
ml |
Y(θ,φ) |
|---|---|---|
0 |
0 |
1 |
1 |
0 |
31/2 cosθ |
1 |
±1 |
(3/2)1/2 senθ e±iφ |
2 |
0 |
(5/4)1/2 (3cos2θ- 1) |
2 |
±1 |
(15/4)1/2 cosθ senθ e±iφ |
2 |
±2 |
(15/8)1/2 sen2θ e±2iφ |
La función angular que representa a un orbital de tipo s es independiente del ángulo, lo que supone que un orbital s presenta simetría esférica. Este orbital se representa normalmente mediante una superficie esférica centrada en el núcleo. Los límites de esta superficie esférica definen la región del espacio para la cual la probabilidad de encontrar al electrón es elevada, generalmente superior al 75%. Cualquier orbital de tipo s se representa con una superficie esférica.
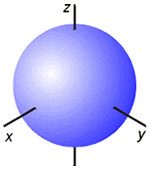
Representación de la parte angular de la función de onda de los orbitales s (probabilidad 75 %)
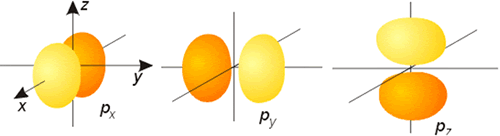
Representación de la parte angular de la función de onda de los orbitales p (probabilidad 75 %)
Todos los orbitales con l >0 poseen amplitudes que varían con el ángulo. Las representaciones gráficas más comunes de los tres orbitales p son idénticas y consisten en dos esferas tangentes en un punto (núcleo). La única diferencia estriba en la orientación de las mismas (según los ejes x, y o z). Cada una de estas representaciones corresponde a un valor del número cuántico ml de los orbitales individuales. La forma de los orbitales d y f se muestran también en las figuras. En en caso de la parte angular de la función de onda, se denomina nodo o superficie nodal al plano del espacio en el que la función se hace cero. De forma general, un orbital caracterizado por un valor del número cuántico l posee l planos nodales. Como puede observarse en las mencionadas figuras, los orbitales de tipo p poseen un plano nodal (que pasa por el núcleo), los orbitales d poseen 2 planos o superficies nodales perpendiculares entre sí y los orbitales f presentan 3 de estos planos nodales.
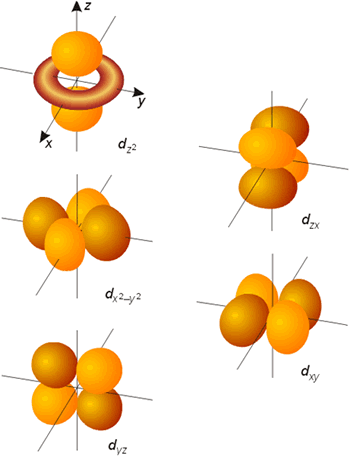
Representación de la parte angular de la función de onda de los orbitales d (probabilidad 75 %).
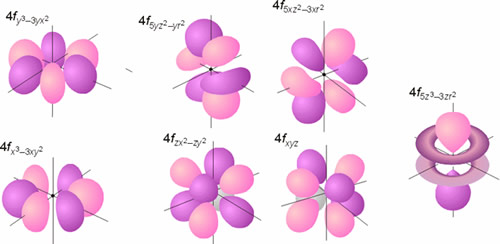
Representación de la parte angular de la función de onda de los orbitales f (probabilidad 75 %)
Hay que señalar que aunque los orbitales s son los únicos que presentan simetría esférica, la suma de la densidad electrónica de los 3 orbitales p, de los 5 orbitales d o de los 7 orbitales f también es esférica. Esto se conoce como teorema de Unsold.
Como se ha comentado ya en varias ocasiones, la función de onda no tiene sentido físico, y ha de acudirse a su cuadrado para obtener alguna información, siempre en términos de probabilidad. Al igual que se describió para la parte radial de la función de onda, también es posible obtener el cuadrado de la parte angular de dicha función, Θ2l,ml (θ) Φ2ml(φ) lo que da lugar a nuevas superficies tridimensionales similares a las representadas anteriormente. Para los orbitales de tipo s, el cuadrado de tal función sigue teniendo simetría esférica, por lo que su representación gráfica no diferiría mucha de la correspondiente a la función angular. Sin embargo, para los orbitales p y d se produce un ligero alargamiento de los lóbulos esféricos ya comentados. De cualquier forma, hay que recalcar que ni las representaciones de Θl,ml (θ) Φml(φ) ni las de Θ2l,ml (θ) Φ2ml(φ) describen ningún orbital, aunque generalmente se emplean como sinónimas de orbitales atómicos.
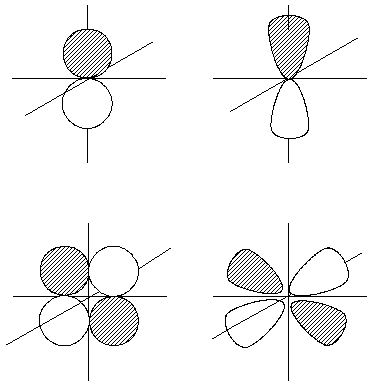
A la izquierda, representación de la parte angular de la función de onda para un orbital p (arriba) y para un orbital d (abajo). A la derecha, representaciones gráficas del cuadrado de dichas funciones.
Así pues, ni la parte radial ni la parte angular de la función de onda, por separado, pueden proporcionar por separado una visión "real" del electrón en el átomo de hidrógeno. La mejor aproximación sería aquella que hiciese uso de Ψ2, incluyendo las dos contribuciones radial y angular. Una manera de representar la probabilidad total es la que se basa en diagramas de contorno, como los que aparecen en la figuras. Las líneas unen todos los puntos que presentan igual valor de densidad electrónica. Los valores de ésta estén siempre referidos al máximo, que se indica con 1.0. En la figura se muestran los diagramas de contorno para el orbital 2pz y 3pz. Obsérvese como en el primer caso existe un plano nodal, que es el plano xy, y ningún nodo radial. En el segundo caso, existe el mismo plano nodal (al ser l = 1 en ambos casos) pero además aparece un nodo radial (n - l - 1 = 1). Los nodos radiales suponen que a esa distancia del núcleo la función de onda se anula, o lo que es lo mismo, existe una superficie esférica a esa distancia que es también una superficie nodal.
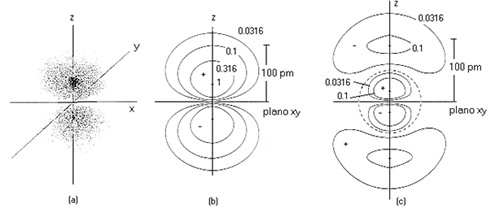
Representación mediante nube de puntos de un orbital p (a) y diagramas de contorno de un orbital 2pz (b) y de un orbital 3pz (c).
Simetría de los orbitales
Anteriormente vimos las figuras de las representaciones gráficas de los orbitales atómicos. En aquellas de los orbitales p, d y f, suelen aparecer signos (+ y -) o dos tipos de colores o rayados en los lóbulos. Ello es debido a que la función de onda puede presentar distinto signo. Por ejemplo, para el orbital pz, el cosθ es negativo para 90º<cosθ<270º (2º y 3er cuadrantes) y positivo en el resto del espacio. Ello supone que el signo de la función de onda es positivo en un lóbulo y negativo en el otro. Los signos de las funciones de onda son muy importantes a la hora de evaluar el solapamiento de dos orbitales de enlace. Por motivos históricos, los orbitales suelen denominarse de tipo gerade o ungerade. Estos vocablos alemanes se aplican, respectivamente, a aquellos orbitales cuyas funciones de onda son simétricas o asimétricas con respecto al centro de inversión. Si al pasar desde un punto de un lóbulo al punto opuesto en otro lóbulo mediante una línea que pase por el centro de coordenadas la función de onda no cambia de signo, entonces es un orbital gerade. Es el caso de los orbitales s y d. Por el contrario, si al efectuar dicha operación la función cambia de signo, se dice que el orbital es de tipo ungerade, lo cual sucede para los orbitales p y f.
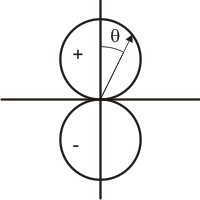
Signo de la función de onda.
En muchos manuales se suele añadir el signo de la función de onda, o un coloreado o rayado distinto a las representaciones del cuadrado de la función de onda, que obviamente es siempre positivo. Esta tendencia no es más que la consecuencia de la importancia que dichos signos tienen en temas relacionados con el enlace químico.