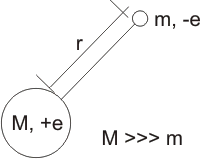
El hidrógeno es el elemento más simple que existe, al constar únicamente de un protón como núcleo y un electrón como corteza. La ecuación de Schrödinger que representa a este sistema es la siguiente:
(∂2Ψ/∂x2) + (∂2Ψ/∂y2) + (∂2Ψ/∂z2) + (8π2m/h2)(E+e2/r)Ψ = 0
puesto que el potencial V = -e2/r.
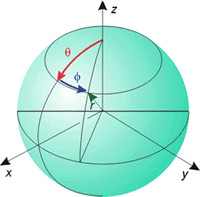
Al ser este un sistema con simetría esférica, es más conveniente utilizar coordenadas polares, para lo que se efectúan los siguientes cambios de variables:
x = r · sen θ· cos φ
y = r · sen θ· sen φ
z = r · cos θ
 |
 |
Coordenadas polares |
El átomo de hidrógeno |
Y de esta forma se pasa de una función de ondas del tipo Ψ(x,y,z) a una del tipoΨ(r,θ,φ).
La resolución de la ecuación de Schrödinger descrita anteriormente conduce a la obtención de tres números cuánticos designados como n, l y ml. El primero de ellos, n, se denomina número cuántico principal y puede tomar valores enteros desde 1 hasta infinito (n = 1, 2, 3...).El segundo, l, es el número cuántico del momento angular orbital (o número cuántico azimutal) y sus valores varían entre 0 y n-1 (l = 0, 1, 2,..., n-1). Finalmente, ml se conoce como el número cuántico del momento magnético, y toma valores comprendidos entre -l y l, ml = -l...,0...,+l (de unidad en unidad). Cada número cuántico caracteriza a una propiedad que está cuantizada en el electrón, es decir, que sólo pueden presentarse en determinados valores: n define la energía, l el momento angular orbital y ml la orientación del momento angular. Las energías permitidas para el electrón en el átomo de hidrógeno dependen sólo y exclusivamente del número cuántico n y vienen dada por la expresión:
E = -(hcZ2R/n2), donde n = 1, 2, 3,..
R es la constante de Rydberg, R = (me4/8h3cε02), por lo que nos queda:
E = -13.6 / n2 (en eV)
La dependencia de E con la inversa de n2 produce una convergencia muy rápida de los niveles de energía a altos valores de E. El nivel de energía cero ocurre cuando n es infinito, situación que corresponde a una separación infinita entre el electrón y el núcleo, es decir, un átomo ionizado. Por encima de este nivel de energía cero el electrón se comporta como una partícula libre que puede viajar con cualquier velocidad y que posee cualquier valor de energía.
Capas, subcapas y orbitales
Cada combinación de los números cuánticos n, l y ml describe una solución de la ecuación de ondas. La solución más simple es aquella en la que n = 1, l = 0 y ml = 0, Ψ(1,0,0), y describe al electrón en el átomo en su estado fundamental (de menor energía). Cada una de estas funciones de onda para el átomo de hidrógeno corresponde a un orbital atómico. En un átomo de hidrógeno todos los orbitales que tienen el mismo valor del número cuántico principal n tienen asociado el mismo valor de la energía y se dice que son orbitales degenerados. El número cuántico principal define una serie de capas del átomo, o conjunto de orbitales con el mismo valor de n y por tanto de la energía. Los orbitales que pertenecen a cada capa se clasifican en subcapas que se distinguen por el valor del número cuántico l.
Así, la capa n = 1 sólo contiene una subcapa con l = 0; la capa n = 2, posee dos subcapas, una con l = 0 y otra con l = 1; la capa n = 3 posee tres subcapas (l = 0, l = 1 y l = 2) y así sucesivamente. Por motivos históricos, se emplean letras para designar las distintas subcapas que dependen del valor del número cuántico l.
Notación de los niveles dependientes de l
l |
0 |
1 |
2 |
3 |
4 |
... |
| s | p | d | f | g | ... |
Una subcapa de número cuántico l consta de 2l+1 orbitales individuales que se distinguen entre sí por el valor del número cuántico ml, el cual puede adoptar 2l+1 valores diferentes, ml = l, l-1... 0...-l. El número cuántico ml especifica la componente del momento angular orbital en un eje arbitrario, generalmente el eje z que pasa a través del núcleo. En términos clásicos ml denota la orientación del orbital ocupado por el electrón. La subcapa p contiene 3 orbitales que se distinguen por los valores ml = 1, 0, -1. La subcapa d consta de cinco orbitales caracterizados por ml = 2,1,0,-1,-2. La siguiente tabla muestra las distintas combinaciones posibles de estos tres números cuánticos hasta n = 2.
Posibles valores de los números cuánticos n, l y ml
n |
1 |
2 |
3 |
|||||||||||
l |
0 |
0 |
1 |
0 |
1 |
2 |
||||||||
ml |
0 |
0 |
+1 |
0 |
-1 |
0 |
+1 |
0 |
-1 |
+2 |
+1 |
0 |
-1 |
-2 |
La función de onda: Parte radial y parte angular
Como se ha mencionado anteriormente, el potencial del núcleo del átomo tiene simetría esférica y la resolución de la ecuación de Schrödinger puede llevarse a cabo mediante el empleo de coordenadas polares. De esta forma se obtienen funciones de onda para cada triada de valores de n, l y ml. Estas funciones de onda están compuestas por varios términos que pueden agruparse de la siguiente forma:
Ψn,l,ml= R n,l(r) Θl,ml (θ) Φml(φ)
La función R(r) se denomina función de onda radial mientras que el producto Θ(θ) Φ(φ) es la función de onda angular. Así pues, la representación de una función de onda requeriría un espacio de cuatro dimensiones, lo que hace inviable "visualizar" dicha función. Por ello resulta útil estudiar por separado las dos funciones mencionadas más arriba: la función radial y la función angular.
3.3. Función de onda radial, función de densidad radial y función de probabilidad radial.
De forma general, la función de onda radial de orbitales hidrogenoides es una expresión del tipo siguiente:
Rnl(r) = f(r)(Z/a0)3/2 e-r/2
donde a0 es el radio de Böhr (0.53 Å) y r = 2Zr/na0 (n = nº cuántico principal). Así, la principal diferencia entre distintos orbitales se produce en f(r). La Tabla 3 muestra los valores de esta función para algunos orbitales.
Función de onda radial: valor de f(r)
n |
l |
f(r) |
|---|---|---|
1 |
0 |
2 |
2 |
0 |
(1
/ 2√2)(2-ρ) |
2 |
1 |
(1
/ 2√6)ρ |
3 |
0 |
(1
/ 9√3)(6-6ρ+ρ2) |
3 |
1 |
(1
/ 9√6)(4-ρ)ρ |
3 |
2 |
(1/ 9√30)ρ2 |
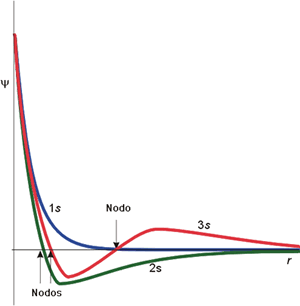
Función de onda radial (orbitales s)
En la figura anterior se
muestra la
variación de la función de onda con el radio para orbitales de tipo s. Todas las funciones radiales, para cualquier valor de
n, presentan una característica común y es que decaen exponencialmente con la
distancia hasta el núcleo. Este decaimiento es tanto más pronunciado cuanto
menor sea el valor del número cuántico n. Otra característica es la
posibilidad de que en algún punto la función de onda se anule. Ello no sucede
para un orbital 1s, pero sí para los orbitales 2s y 3s. Estos valores para los
que la función de onda radial se hace cero se denominan nodos radiales. En
un nodo, la probabilidad de encontrar al electrón es siempre nula. Un
orbital con números cuánticos n y l presenta
n-l-1 nodos radiales, independientemente del valor de ml.
Así, el orbital 2s (n = 2, l = 0 y ml = 0)
posee sólo un nodo radial mientras que el orbital 3s (n = 3, l = 2, ml = 0) presenta 2 nodos radiales.
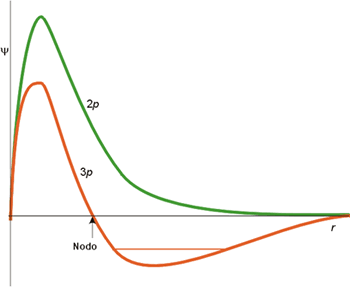
Función de onda radial (orbitales p)
Esta figura muestra la función de onda radial de los orbitales 2p y 3p. El orbital 2p (n = 2, l = 1) no presenta nodos radiales porque su función de onda radial no se hace cero en ningún momento, salvo para r = 0. Esta característica, la de R(r) = 0 para r = 0, es general para todos los orbitales que no sean de tipo s. El orbital 3p presenta un nodo radial, como corresponde por sus valores de n (3) y l (1).
De la expresión de la función radial es posible obtener el valor o valores de r para los que la función de onda se anula. Así, por ejemplo, el nodo del orbital 2s aparece a r= 0.53 Å.
Es conveniente recordar que la función de onda no tiene significado físico alguno, y que es el cuadrado de dicha función el que proporciona información acerca de la probabilidad de encontrar al electrón. La función R2 se denomina función de densidad radial, puesto que su valor es proporcional a la densidad electrónica.
Funciones de densidad radial y de probabilidad radial para el orbital 1s.
La figura muestra la variación de esta función con respecto de la distancia para un orbital 1s. La máxima densidad electrónica se produce en el núcleo, y va descendiendo al aumentar r. Ello es aplicable para cualquier orbital s. Sin embargo, para el resto de orbitales (p, d, f), la función de densidad radial es nula para r = 0, pues R(r) = 0 en dicho punto.
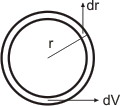Una
forma alternativa de unir función de onda y probabilidad es calcular la
probabilidad de encontrar al electrón en una esfera de radio r y espesor dr. El volumen de esta capa de espesor infinitesimal sería dV.
Partiendo del volumen de la esfera
V = 4πr3/3
y pasando a diferenciales, queda
dV = 4πr2dr
Multiplicando a ambos lados por la función de densidad radial, R2(r):
R2(r)dV = 4πr2 R2(r)dr
que se denomina función de probabilidad radial (o función de distribución radial). Este no es más que el resultado de aplicar la condición de Born, pues la probabilidad de encontrar al electrón en un elemento de volumen entre r y dr en un entorno esférico viene dada por la integral de Y2 para cualquier valor de los ángulos q y f:
| π ∫ 0 |
2π ∫ 0 |
Ψ2sen θ dθ dφ r2 dr = 4πr2 R2(r)dr |
Anteriormente vimos una gráfica donde aparecen representadas la función de probabilidad radial. Debido a que para un orbital 1s la función de densidad radial decae exponencialmente con la distancia al núcleo mientras r2 aumenta, la función de probabilidad radial (4πr2R2) para dicho orbital posee un máximo como se muestra en la figura. Es decir, existe una distancia r del núcleo en la que existe una mayor probabilidad de que se "encuentre" el electrón (no se olvide el principio de incertidumbre). Para un orbital 1s de un átomo hidrogenoide el máximo de la función de probabilidad radial aparece a rmax = (a0/Z), rmax = 0,529 Å. Este valor concuerda exactamente con el radio de Böhr.
La distancia más probable para encontrar al electrón aumenta con el valor de n porque a medida que aumenta la energía del orbital existe una mayor probabilidad de encontrar al electrón en zonas más alejadas del núcleo. Así para el orbital 2s existen dos máximos de la función de probabilidad radial, uno de menor intensidad a r = 0.8 a0 y otro, de mayor intensidad, a r = 5.2 a0. También existe un nodo, donde la probabilidad de encontrar al electrón es cero, para r = 2a0. Como se observa en la siguiente figura existe una mayor probabilidad de encontrar al electrón en las cercanías del núcleo para orbitales de tipo s que para los de tipo p. Por ello se dice que los orbitales s son más penetrantes que los orbitales p, un concepto sobre el que se incidirá más adelante.
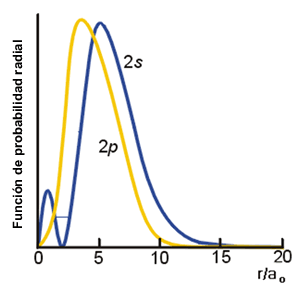
Función de probabilidad radial de los orbitales 2s y 2p
Una cuestión que suele plantear dificultades de comprensión es la siguiente: ¿cómo puede "pasar" el electrón desde la zona de la izquierda del nodo a la de la derecha, si la probabilidad de que esté en el nodo es cero? La respuesta es simple: la naturaleza ondulatoria del electrón le hace "existir" en los dos lados del nodo a la vez. La anterior pregunta surge al aplicar el concepto clásico de electrón como partícula, lo cual no es aplicable.