Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
Por todas partes se repite y se expresa una y otra vez, que el espacio tiempo se curva en presencia de masa y que la curvatura de este crea gravedad. Pues este artículo plantea de manera sorprendente que en realidad el espacio-tiempo se curva incluso en presencia solo de un observador aún sin masa, es decir que los cuerpos delante de un observador siguen una trayectoria espacial relativamente curva. En este artículo se explica en este orden de ideas, la razón del por qué el espacio-tiempo se curva alrededor de la masa como observadora. Presentamos como una de las pruebas al parecer demasiados extraordinarios y contundentes de que el espacio-tiempo se curva en presencia del observador, describimos tras ello en este artículo, una trascendental demostración del efecto Doppler relativista. Sería demasiado interesante que por las pupilas de cualquier físico, por muy concentrado o desconcentrado que se encuentre por alguna razón, se ocupe de esta descripción del Doppler relativista descrito por intermedio de la curvatura del espacio tiempo para el observador.
Palabras claves: Gravedad Cuántica, Relatividad General, Relatividad Especial, Efecto Doppler Relativista, Corrimiento al Rojo gravitacional.
Abstract
Everywhere is repeated and expressed again and again, that space time curves in the presence of mass and the curvature of this creates gravity. Because this article poses surprisingly really space-time curves even in the presence of an observer not mass, yet only i.e. bodies ahead of an observer to remain a relatively curved space path. This article explains in this vein, the right of the why the space-time curves around the mass as an observer. Presented as one of the tests seems too extraordinary and compelling that space-time curve in the presence of the observer, we describe in this article, a transcendental demonstration of the relativistic Doppler Effect after that. It would be too interesting that for the pupils of any physical, for very concentrated or desconcenter is for some reason, deal with this description of the relativistic Doppler described the curvature of space through time to the observer.
Key Words: Quantum Gravity, General Relativity, Special Relativity, Doppler Effect Relativist, Red landslide to the gravitational one.
1. Introducción
El espacio-tiempo es la entidad geométrica en la cual se desarrollan todos los eventos físicos del Universo, de acuerdo con la teoría de la relatividad y otras teorías físicas. Las líneas más "rectas" posibles de un espacio-tiempo se llaman líneas geodésicas que son líneas de curvatura mínima. El nombre alude a la necesidad de considerar unificadamente la localización geométrica en el tiempo y el espacio, ya que la diferencia entre componentes espaciales y temporales es relativa según el estado de movimiento del observador. De este modo, se habla de continuo espacio-temporal.
Aquí recordamos también en esta introducción que de la siguiente manera asimismo quedó expresada en el artículo taquión gravitatorio, una relación que describe con respecto a la componente vcosθ el comportamiento de una partícula que se aleja del observador:
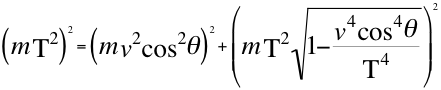 (1)
(1)
Donde m es la cantidad de masa invariante de la partícula que se observa alejándose,T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, θes el ángulo descrito entre la trayectoria de la partícula y el observador.
Ahora detallamos una relación que describe el movimiento de una partícula que se acerca al observador con respecto a la componente vcosθ:
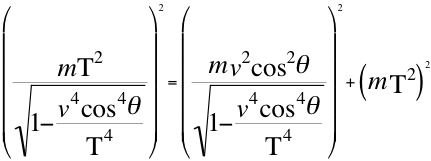 (2)
(2)
Donde m es la cantidad de masa invariante de la partícula que se observa acercándose,T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, θes el ángulo descrito entre la trayectoria de la partícula y el observador.
Estas dos anteriores ecuaciones número uno (1) y dos (2) podemos expresarla de la siguiente manera en función eso si de la energía invariante E, la energía cinética Ec y la energía potencial gravitatoria Ep:
![]() (3)
(3) ![]() (4)
(4)
Donde E es la cantidad de energía invariante de la partícula que se observa alejándose o acercándose al observador, Ec es la energía cinética relativa de la partícula que se aleja o se acerca al observador y Ep es la energía potencial gravitatoria relativa de la partícula que se aleja o se acerca al observador.
La energía invariante con respecto a la velocidad del taquión E=m.T2 de una partícula es constante y es equivalente en energía a la masa invariante de la partícula:
![]() (5)
(5)
Donde E es la energía invariante de la partícula, m es la masa invariante de la partícula y T es la velocidad del taquión.
Partimos diciendo que en la relación gravitacional de Newton podemos expresarla en función de la energía Ep potencial gravitatoria:
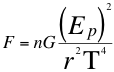 (6)
(6)
Donde F es la fuerza de atracción mutua, n es un escalar que define la relación de las energías invariantes de los objetos, Ep es la energía potencial gravitatoria del objeto observado, G es la constante de gravitación universal, T es la velocidad del taquión, r es la distancia que separa los centros de gravedad de ambos objetos.
2. Desarrollo del Tema.
Al comenzar el desarrollo de este artículo nos es pertinente aclara que, el concepto de “observador” que vamos a utilizar en este trabajo, es aquel sistema sensible simultáneamente tanto a las manifestaciones electromagnéticas de la partícula que se observa como a las manifestaciones gravitatorias del mismo objeto que se observa.
En una Relatividad general la relación de energía-momento de una partícula que se mueve en el espacio-tiempo, serían aquellas dos ecuaciones que relacionarían para un determinado observador, las componentes relativas de vector energía-momento relacionada con respecto a la masa en reposo, de la respectiva partícula que correspondientemente se mueve respecto a ese observador.
Cuando una partícula se aleja o se acerca de un observador en cualquier dirección y sentido su velocidad v, se podrá descomponer en dos componentes perpendiculares entre sí descritas con respecto al ángulo de observación: Una componente vcosθ útil para el estudio del Doppler relativista, componente que se situará externa o internamente en la misma dirección radial o recta de visión que tiene el segmento de recta que une a la respectiva partícula con el pertinente observador, y otra componente vsenθ que quedará siempre totalmente tangencial al círculo imaginario en torno al observador y será perpendicular a la mencionada recta de visión anterior.
![]() (7)
(7)
Donde v es la velocidad en el espacio-tiempo de la partícula observada, θ es el ángulo que describe la velocidad con la componente que directamente se aleja o se acerca de la partícula.
CUANDO UNA PARTÍCULA SE ALEJA DEL OBSERVADOR
Vamos a referirnos primero al caso cuando una partícula se aleja del observador, entonces la componente vcosθ de la velocidad, por su lado describirá su energía cinética mv2cos2θ, estará en dirección exterior a la misma recta radial de visión o dirección visual que precisamente une a la partícula con el observador, esa componente pues va a estar dirigida directamente alejándose en ángulo 180 grados con respecto al observador y será externa a la curvatura imaginaria alrededor del observador.
La componente vsenθ por su otro lado, va a estar alejándose también pero relativa y mínimamente en uno de los dos sentidos totalmente tangencial y exterior también a la curvatura imaginaria del espacio-tiempo que circunscribe al observador y será además perpendicular a la anterior recta de visión de ese observador, será paralela incluso y con el mismo origen del vector Ec=mv2sen2θ de la energía cinética tangencial y relativa para ese observador. Esa componente va a estar alejándose en dirección que describe un ángulo de 90 grados con respecto al observador.
Aparece el vector Ep de la energía potencial gravitatoria ortogonal con respecto a la velocidad tangencial vsenθ relativa al observador, que seguidamente vamos a recordar inmediatamente para este observador en la siguiente relación número ocho (8):
 (8)
(8)
Donde E es la cantidad de energía invariante de la partícula que se observa alejándose del observador, m es la masa invariante de la partícula observada, Ep que es la energía potencial gravitatoria relativa de la partícula que se aleja al observador, v que es la velocidad de la partícula en el espacio tiempo, T que es la velocidad del taquión, θ es el ángulo descrito entre la velocidad de la partícula y la componente que directamente se aleja del observador.
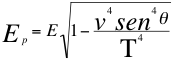 (8)
(8)
Este cuarto vector inercial del tiempo para ese observador respecto a esa velocidad tangencial sería, totalmente perpendicular al vector de la exterior energía cinética tangencial relativa, además ese cuarto vector estará en su afán dirigiéndose y buscado totalmente al observador y representa exactamente a la energía invariante de la partícula pero estará contraída por la velocidad en el tiempo, ese cuarto vector será precisamente la energía potencial gravitatoria Ep relativa de la partícula dirigido directamente hacia ese observador.
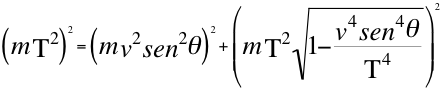 (9)
(9)
![]() (3)
(3)
Donde m es la masa invariante de la partícula, T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, Ep es el módulo del vector de energía potencial gravitatoria relativa, E es el módulo del vector energía invariante equivalente de la partícula observada, Ec es el módulo del vector energía cinética tangencial relativa, θ es el ángulo que describe la velocidad con la componente que directamente se aleja del observador.
Vale la pena hacer la observación de que a pesar de que el vector Ep de la energía potencial gravitatoria de la partícula que se aleja, es un vector totalmente dirigido hacia el respectivo observador, hace parte también como una de las dos componente del vector E resultante de la energía invariante que describe un ángulo α con la energía potencial gravitatoria, describen entre sí un ángulo α de curvatura supremamente insignificante casi de cero grados y abierto hacia el observador:
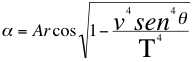 (10)
(10)
Donde α es el ángulo abierto hacia el observador descrito entre la energía potencial gravitatoria Ep y la resultante energía invariante E de la partícula observada alejándose.
CUANDO UNA PARTÍCULA SE ACERCA AL OBSERVADOR
Vamos a referirnos ahora en segundo lugar es al caso cuando una partícula, se estudia ahora por un observador que se le acerca a dicha partícula entonces, esa componente vcosθ de la velocidad por un lado ubicada haciendo parte ya de la recta radial interna de visión o dirección visual que precisamente une a la partícula con el respectivo observador, va a estar en este caso es dirigida directamente buscando al observador y tendrá la misma dirección, sentido y punto de aplicación que la energía potencial gravitatoria Ep de la partícula descrita respecto a la velocidad tangencial en la anterior relación número nueve (9). Este vector vcosθ quedará circunscrito y totalmente interno al círculo imaginario de curvatura alrededor del observador. Esa componente vcosθ en este caso, va a describir un ángulo de cero grados con respecto al observador.
La otra componente vsenθ por su otro lado para ese observador, va a estar y seguir totalmente perpendicular a la recta de visión descrita anteriormente, será de dirección y sentido tangencial y totalmente exterior a la curvatura imaginaria del espacio-tiempo en torno a ese observador por lo que definitivamente se alejará del observador y será paralela exterior y con el mismo punto de aplicación que el vector de la energía cinética tangencial también exterior y relativa al observador Ec=mv2sen2θ. Este vector vsenθ y Ec=mv2sen2θ en este caso se alejarán definitivamente del observador. Vale la pena observar que a pesar de que la partícula se acerca al observador la componente tangencial vsenθ se aleja. Esta componente en este caso también va a seguir describiendo un ángulo de 90 grados con respecto al observador.
![]() (11)
(11)
Donde m es la cantidad de masa invariante de la partícula que se observa acercándose,T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, θes el ángulo descrito entre la velocidad y la componente que se acerca directamente al observador.
El cuarto vector del tiempo con respecto a vsenθ, como la vsenθ de la partícula se aleja tangencialmente del observador describirá entonces, un vector dirigido hacia el observador de la energía potencial gravitatoria Ep de la partícula, perpendicular al vector de la energía cinética tangencial relativa y de su suma vectorial entonces precisamente resultará, la energía invariante E de la partícula que se mueve:
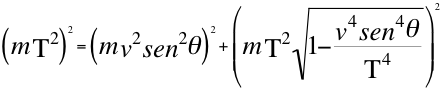 (9)
(9)
![]() (3)
(3)
Donde m es la cantidad de masa invariante de la partícula que se observa acercándose,T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, θes el ángulo descrito entre la velocidad de la partícula y la componente que directamente se acerca al observador, Ep es el módulo del vector de energía potencial gravitatoria relativa, E es el módulo del vector energía invariante de la partícula observada, Ec es el módulo del vector de energía cinética tangencial relativa.
Vale la pena hacer la observación de que a pesar de que el vector Ep de la energía potencial gravitatoria de la partícula que se acerca al observador, es un vector totalmente dirigido hacia el respectivo observador, sigue siendo una de las dos componente del vector E resultante de la energía invariante que describe un ángulo α con la energía potencial gravitatoria, supremamente insignificante casi de cero grados y abierto hacia el observador igual al descrito cuando la partícula se aleja:
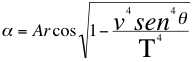 (10)
(10)
Donde α es el ángulo abierto hacia el observador descrito entre la energía potencial gravitatoria Ep y la resultante energía invariante E de la partícula observada aproximándose esta vez.
Como cualquier magnitud física que sea función de la velocidad, la energía cinética y la relación total de energía-momento de un objeto, no solo dependen de la naturaleza interna de ese objeto, también dependen tanto de la naturaleza interna del observador y la profunda relación entre el objeto y el determinado observador, por lo tanto no pueden ser independientes de él como al parecer se pretende entender de Einstein en la física actual.
Hasta ahora hemos descrito el análisis de observadores que por su naturaleza interna son incapaces de colapsar la función de onda. Se puede observar que cuando una partícula se aleja del observador, las dos componentes de la velocidad también se alejan quedando ambas totalmente exteriores al círculo imaginario de la curvatura del espacio tiempo alrededor del observador pero, no sucede igual cuando una partícula es descrita acercándose al observador, las dos componentes que constituyen la velocidad, una de ella es tangencial y contrariamente también se aleja relativamente en alguna medida dl observador, quedando totalmente exterior al círculo imaginario entorno a la curvatura del espacio tiempo alrededor del observador, la otra componente se acerca directamente al observador y queda dentro de la curvatura imaginaria alrededor del observador.
LO QUE SUCEDE CUANDO EL OBSERVADOR POSEE MASA
Pero qué pasa si el observador tiene masa? Es claro que el reposo absoluto no existe y el movimiento en el universo de una partícula depende también del movimiento relativo del observador. Entonces tanto objeto observado como observador, tendrán un entorno lleno de distintos vectores particulares de energía potencial gravitatoria, energías invariantes y distintos vectores de energía cinética relativa. Cuando el observador tiene masa, se presenta a la sazón una sinergia de fuerzas por que se comportan entonces los dos cuerpos, como dos mutuos observadores que recíprocamente se observan y atraen colapsándose entre sí recíprocamente en alguna cantidad la respectiva función de onda. Los vectores sensibles a la fuerza gravitacional con dirección y sentido directo entre observadores, responden pues con atracción gravitatoria entre los vectores Ep relativo es decir, el de la energía potencial gravitatoria de ambas masas que se observan mutuamente. Entonces el espacio-tiempo en torno a una masa observadora sigue igualmente curvado.
Cuando la partícula observada y el observador poseen masa, ambos estarían dotados de la misma naturaleza interna capaz de influir en los movimientos recíprocos de cada uno de ellos. Entre ambos objetos entonces se establece un campo gravitatorio con varias líneas de flujo que viajarían a la velocidad del taquión.
Cuando las masas se alejan o se acercan entre sí, se cumple la siguiente relación de Newton número seis (6) con atracción directa por intermedios de los vectores mutuos de la energía potencial gravitatoria Ep de ambas masas.
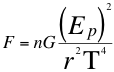 (6)
(6)
Donde F es la fuerza de atracción mutua, n es un escalar que define la relación de las energías invariantes de los objetos, Ep es la energía potencial gravitatoria relativa del objeto observado, G es la constante de gravitación universal, T es la velocidad del taquión, r es la distancia que separa los centros de gravedad de ambos objetos.
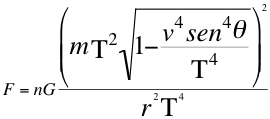 (6)
(6)
Donde F es la fuerza de atracción mutua, n es un escalar que define la relación de las energías invariantes de los objetos, m es la masa invariante del objeto observado, E es la energía invariante de la partícula observada, G es la constante de gravitación universal, θ es el ángulo del observador con la trayectoria del objeto observado, T es la velocidad del taquión, r es la distancia que separa los centros de gravedad de ambos objetos.
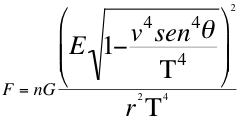 (6)
(6)
Cuando las masas se acercan o se alejan del observador el valor de las respectivas energías potenciales gravitatorias que dependen del ángulo θ y la velocidad para ese observador con respecto a vsenθ quien dice como debe curvarse el espacio tiempo para él. El movimiento orbital de un cuerpo lo describe o gira alrededor del valor tomado por el ángulo θ como se puede ver, que él fluctúa entre valores cercanos a 90 grados. Cuando la masa que orbita se aleja, el ángulo θ es mayor de 90 grados pero, cuando se acerca el ángulo se reduce a menos de 90 grados.
Igualmente sucede con la relación que describe el movimiento relativo de un fotón que se aleja del observador, descrito en las siguientes relaciones con respecto a vcosθ y vsenθ:
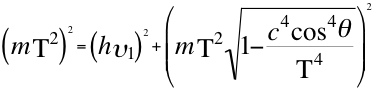 (12)
(12)
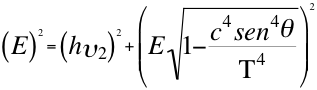 (13)
(13)
![]() (3)
(3)
Donde m es la masa invariante de la partícula, T es la velocidad del taquión, Ep es el módulo del vector de energía potencial gravitatoria, E es el módulo del vector energía invariante de la partícula observada, Ec es el módulo del vector energía cinética relativa, θ es el ángulo que describe la velocidad con la componente que directamente se aleja de la partícula, h es la constante de Planck, υ es la frecuencia relativa del fotón para ese observador, c la velocidad de la partícula de luz o electromagnética.
Igualmente sucede con la relación que describe el movimiento relativo de un fotón que esta vez se acerca al observador, descrito en la siguiente relación con respecto a vcosθ y vsenθ:
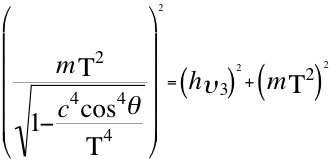 (14)
(14)
![]() (4)
(4)
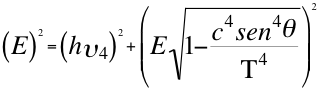 (15)
(15)
![]() (3)
(3)
Donde m es la masa invariante de la partícula, T es la velocidad del taquión, Ep es el módulo del vector de energía potencial gravitatoria, E es el módulo del vector energía invariante de la partícula observada, Ec es el módulo del vector energía cinética relativa, θ es el ángulo que describe la velocidad con la componente que directamente se aleja de la partícula, h es la constante de Planck, υ es la frecuencia relativa del fotón para ese observador, c la velocidad de la partícula de luz u onda electromagnética.
Aunque hasta ahora todos los datos experimentales son consistentes con un fotón de masa cero en particular, investigaciones recientes tienen cotas de mayor precisión en los experimentos para los límites superiores de una hipotética masa del fotón. Sin embargo los límites superiores aceptados universalmente de la masa del fotón son 1,1x10-52kg, cuestión que concuerda demasiado con la eventualidad de existir un taquión gravitatorio ubicado en cuanto a su velocidad muy cerca del techo de la velocidad de la luz.
3. Conclusiones.
a)-Para un observador hacer la descripción correcta del movimiento de una partícula, necesita por lo menos dos ecuaciones complementarias de energía-momento, entonces cuando una partícula se aleja de un observador ese movimiento será descrito por ese observador mediante dos ecuaciones, una de ellas será la relación número uno (1) que describe la energía cinética de alejamiento con respecto a vcosθ y la otra ecuación será la relación número nueve (9) que sirve por que describe la energía potencial relativa de acercamiento gravitatorio para ese observador con respecto a vsenθ:
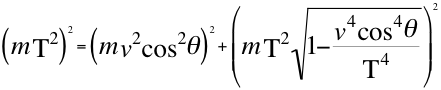 (1)
(1)
Donde m es la cantidad de masa invariante de la partícula que se observa alejándose,T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, θes el ángulo descrito entre la trayectoria de la partícula y el observador.
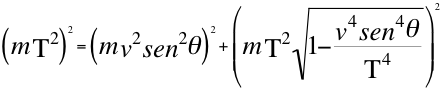 (9)
(9)
![]() (3)
(3)
Donde m es la masa invariante de la partícula, T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, Ep es el módulo del vector de energía potencial gravitatoria, E es el módulo del vector energía invariante equivalente de la partícula observada, Ec es el módulo del vector energía cinética tangencial relativa, θ es el ángulo que describe la velocidad con la componente que directamente se aleja del observador.
b)-Cuando una partícula se acerca al observador ese movimiento será descrito por ese observador con las siguientes dos relaciones complementarias de energía-momento, una de ellas será la ecuación número dos (2) que describe el movimiento de acercamiento con respecto a la energía cinética mv2cos2θ y la otra relación que es descrita nuevamente por la misma relación número nueve (9) que sirve reiteradamente por que describe a la energía potencial gravitatoria de acercamiento con respecto a vsenθ:
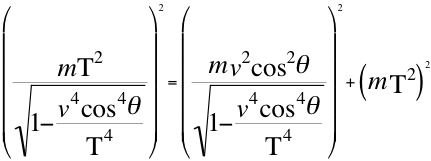 (2)
(2)
![]() (4)
(4)
Donde m es la cantidad de masa invariante de la partícula que se observa acercándose,T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, Ep es el módulo del vector de energía potencial gravitatoria relativa, E es el módulo del vector energía invariante equivalente de la partícula observada, Ec es el módulo del vector energía cinética tangencial relativa, θes el ángulo descrito entre la trayectoria de la partícula y el observador.
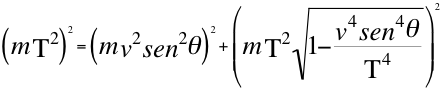 (9)
(9)
![]() (3)
(3)
Donde m es la masa invariante de la partícula, T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, Ep es el módulo del vector de energía potencial gravitatoria relativa, E es el módulo del vector energía invariante equivalente de la partícula observada, Ec es el módulo del vector energía cinética tangencial relativa, θ es el ángulo que describe la trayectoria de la velocidad de la partícula con la componente que directamente se acerca al observador.
c)-Como gran conclusión de este trabajo y como prueba de que realmente el espacio-tiempo se curva alrededor del observador, hacemos el análisis del Doppler relativista descrito por un observador sin masa y que tiene el mismo potencial gravitacional de la fuente:
Cuando una fuente se acerca al observador sin masa, la velocidad de la fuente se puede descomponer en sus dos componentes ortogonales, estas en función del ángulo descrito por el observador con respecto a la trayectoria de la fuente observada. Una componente vcosθ que irá dirigida acercándose al azul directamente al observador y la otra componente ortogonal vsenθ, que aunque mínimamente siempre se alejará corrida hacia el rojo del observador. Entonces el Doppler relativista se obtendrá de la relación entre las dos componentes es decir, la relación entre la componente que se aleja corrida hacia el rojo sobre, la componente que se acerca corrida hacia el azul, descritos de la siguiente manera en la siguiente relación para una fuente que se acerca:
 (16)
(16)
Donde υo es la frecuencia original de la onda electromagnética emitida por la fuente, υ es la frecuencia tal como la mediría un observador que se acerca relativamente a la fuente con respecto a la velocidad transversal vcosθ pero que se aleja también relativamente de la fuente con respecto a la otra componente de velocidad transversal de vsenθ, también v es la velocidad de la fuente en el espacio tiempo, θ es el ángulo descrito entre la dirección visual del observador y la trayectoria de la fuente, T es la velocidad del taquión.
Cuando el observador está situado en la misma trayectoria de una fuente que a cierta distancia se acerca corrida toda puntualmente hacia el azul, con θ=0, queda la relación del Doppler relativista de la siguiente manera:
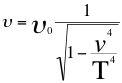 (17)
(17)
Donde υo es la frecuencia original de la onda electromagnética emitida por la fuente, υ es la frecuencia tal como la mediría un observador que se acerca directamente ubicado en la misma trayectoria de la fuente respectivamente a la velocidad de la fuente, también v es la velocidad de la fuente en el espacio tiempo, T es la velocidad del taquión.
Si la fuente está totalmente al frente del observador en un ángulo de 90 grados con el respectivo observador, describiendo un Doppler transversal, entonces la relación del Doppler relativista quedaría corrida totalmente hacia el rojo de la siguiente manera:
 (18)
(18)
Donde υo es la frecuencia original de la onda electromagnética emitida por la fuente, υ es la frecuencia tal como la mediría un observador que se encuentra ubicado precisamente de manera simultánea enfrente de la fuente, v es la velocidad de la fuente en el espacio tiempo, T es la velocidad del taquión.
Si la fuente ya pasó por el frente del observador y se está respectivamente alejando del mismo a cierta distancia, entonces ambas componentes vcosθ y vsenθ están corridas hacia el rojo y se cumple entonces la siguiente relación:
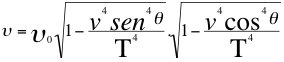 (19)
(19)
Donde υo es la frecuencia original de la onda electromagnética emitida por la fuente, υ es la frecuencia tal como la mediría un observador que se encuentra ya alejándose de la fuente, v es la velocidad de la fuente en el espacio tiempo, T es la velocidad del taquión.
Si el observador se encuentra ubicado ahora en la misma trayectoria de una fuente que respectivamente se aleja totalmente del referido observador, entonces la relación del Doppler relativista quedará toda corrida hacia el rojo de manera puntal de la siguiente manera:
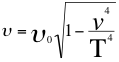 (20)
(20)
Donde υo es la frecuencia original de la onda electromagnética emitida por la fuente, υ es la frecuencia tal como la mediría un observador que se encuentra ubicado precisamente en la trayectoria de la fuente que se aleja a su respectiva velocidad, v es la velocidad de la fuente en el espacio tiempo, T es la velocidad del taquión.
d)-Cuando un observador sin masa y objeto observado, tienen diferentes potenciales gravitacionales.
Para seguir demostrando lo acertado que es considerar al espacio-tiempo curvado alrededor del observador, recurrimos en esta explicación también al conocido experimento de Pound Rebka en la cual, el observador se encuentra a mayor altura de la fuente y sabemos que ambos están en reposo relativo pero en realidad, ambos fuente y observador tienen velocidades diferentes en el espacio-tiempo. Para ese observador de mayor altura, que siente atracción gravitatoria hacia la fuente por lo tanto él tiende acercarse y a ubicarse en la relación del experimento hacia el azul. Sin embargo la fuente tiende a alejarse tangencialmente de la curvatura imaginaria alrededor del observador y esto se traduce corrido hacia el rojo en la relación que describe el experimento, por lo tanto toda la relación está corrida hacia el rojo:
 (21)
(21)
Donde υo es la frecuencia original de la onda electromagnética emitida por la fuente, υ es la frecuencia tal como la mediría un observador que se encuentra a cierta altura de la fuente, G es la constante de gravitación universal, M es la masa generadora del campo gravitatorio, t es el tiempo propio, R es el radio del observador en el campo gravitatorio, r es el radio de la fuente en el campo gravitatorio, T es la velocidad del taquión.
R > r
Cuando es lo contrario, el observador se instala en la superficie del planeta por ejemplo y la fuente está ahora ubicada en reposo a cierta altura sobre el observador y en el mismo campo gravitacional. Aunque el observador está corrido hacia el azul tendiendo de acercarse a la fuente, esta al alejarse de la curvatura imaginaria del observador está corrida hacia el rojo por lo tanto toda la relación estará corrida hacia el azul.
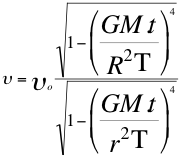 (22)
(22)
Donde υo es la frecuencia original de la onda electromagnética emitida por la fuente, υ es la frecuencia tal como la mediría un observador que se encuentra en la superficie del planeta, G es la constante de gravitación universal, M es la masa generadora del campo gravitatorio, t es el tiempo propio, R es el radio de la fuente en el campo gravitatorio, r es el radio del observador en el campo gravitatorio, T es la velocidad del taquión.
R > r
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[01] Relatividad General
[02] Relatividad General
[03] corrimiento al rojo gravitacional
[04] efecto Doppler relativista
[05] corrimiento al rojo
[06] corrimiento al rojo gravitacional
[07] efecto doppler relativista
[08] efecto doppler relativista
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
[15] http://www.monografias.com/trabajos-pdf2/matematicas-energia-cinetica-potencial-movimiento/matematicas-energia-cinetica-potencial-movimiento.pdf
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.