Resumen
En este trabajo se encuentra una ecuación matemática donde con ella se esclarece y se confirma que todos los movimientos en la superficie de un cuerpo masivo o planeta como la Tierra, incluso movimientos de objetos a velocidades tan simples y comunes como la velocidad de un automóvil, la velocidad de una pelota de beisbol, la de un avión como la de un fotón, pueden ser expresadas en el universo como velocidades cósmicas, ya que la descripción de este trabajo alcanza relacionar al cuadrado de la velocidad de los cuerpos, con el cuadrado de la velocidad orbital que tiene el punto preciso por donde justamente se mueve dicho objeto dentro del campo gravitatorio. Es tan certera dicha relación que sirve para calcular de paso con ella tanto a la primera velocidad cósmica del planeta como su segunda velocidad cósmica o de escape.
Palabras claves: Velocidad orbital, Agujero Negro, Primera velocidad cósmica, Velocidad de escape.
Abstract
This work is a mathematical equation where it it clarifies and confirms that all movements on the surface of a massive body or planet like the Earth, even movements of objects at speeds so simple and common as the speed of a car, the speed of a baseball ball, a plane as a photonthey can be expressed in the universe as cosmic speeds, since the description of this work reaches relate to the square of the speed of the bodies, with the square of the orbital speed which has the precise point where just moves the object within the gravitational field. It is so accurate that relationship which serves to calculate step with her both the first cosmic velocity of the planet as its second Cosmic Velocity or escape.
Keywords: Orbital speed, black hole, first Cosmic Velocity, escape velocity.
1. Introducción
En esta corta introducción vamos a recordar al cuadrivector y cuadrivelocidad del trabajo “Sobre gravedad cuántica en la relatividad general.
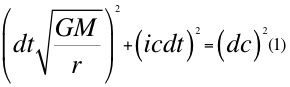
Donde dt es el diferencial del tiempo, G es la contante gravitacional universal, M es la masa del cuerpo másico, r es la distancia radial hasta el centro del cuerpo másico, i es el número imaginario, dc es la diferencial del espacio de la velocidad de la luz y c es la velocidad de la luz en el vacío.
En esta anterior ecuación vamos a continuar simplificando y nos quedaría de la siguiente manera:
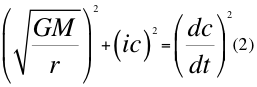
Donde G es la contante gravitacional universal, M es la masa del cuerpo másico, r es la distancia radial hasta el centro del cuerpo másico, i es el número imaginario, dc es la diferencial del espacio de la velocidad de la luz, dt es el diferencial del tiempo y c es la velocidad de la luz en el vacío.
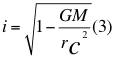
Donde i es el número imaginario, G es la contante gravitacional universal, M es la masa del cuerpo másico, r es la distancia radial hasta el centro del cuerpo másico y c es la velocidad de la luz en el vacío.
Nos queda entonces el cuadrivector del espacio-tiempo de la relatividad general queda de la siguiente manera:
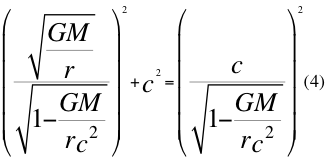
Donde G es la contante gravitacional universal, M es la masa del cuerpo másico, r es la distancia radial hasta el centro del cuerpo másico y c es la velocidad de la luz en el vacío.
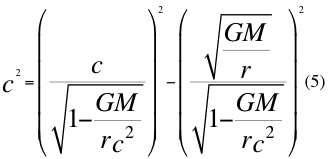
Donde G es la contante gravitacional universal, M es la masa del cuerpo másico, r es la distancia radial hasta el centro del cuerpo másico y c es la velocidad de la luz en el vacío.
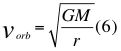
Donde vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico y r es la distancia radial del punto del campo al centro del cuerpo másico.
En esta relación anterior número cinco (5) se introduce la masa en reposo como un escalar para encontrar a la cantidad de movimiento de la relatividad general:
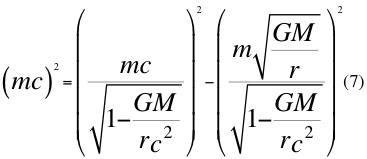
Donde m es la masa en reposo de un objeto cualquiera, G es la contante gravitacional universal, M es la masa del cuerpo másico, r es la distancia radial hasta el centro del cuerpo másico y c es la velocidad de la luz en el vacío.
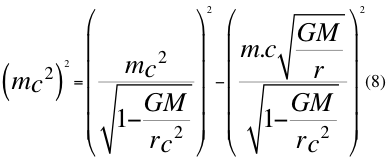
Donde m es la masa en reposo de un objeto cualquiera, G es la contante gravitacional universal, M es la masa del cuerpo másico, r es la distancia radial hasta el centro del cuerpo másico y c es la velocidad de la luz en el vacío.
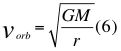
Donde vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico y r es la distancia radial del punto del campo al centro del cuerpo másico
De esta anterior relación número ocho (8) tomamos el último componente del extremo derecho del miembro derecho y lo desarrollamos en la relatividad especial:
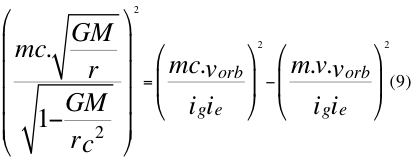
Donde m es la masa en reposo de un objeto cualquiera, G es la contante gravitacional universal, M es la masa del cuerpo másico, r es la distancia radial hasta el centro del cuerpo másico, vorb es la velocidad orbital, ig es un número imaginario de la relatividad general, ie es el número imaginario de la relatividad especial, v es la velocidad de la partícula y c es la velocidad de la luz en el vacío.
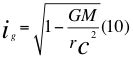
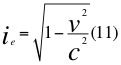
Donde ig es el número imaginario de la relatividad general, G es la contante gravitacional universal, M es la masa del cuerpo másico, ie es el número imaginario de la relatividad especial, v es la velocidad de la partícula y c es la velocidad de la luz en el vacío.
Remplazando la anterior ecuación número nueve (9) en la también anterior relación número ocho (8) nos resulta la siguiente gran relación global de gravedad cuántica:
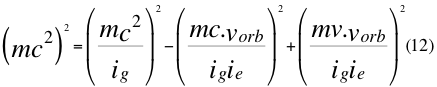
Donde m es la masa en reposo de un objeto cualquiera, ig es número imaginario de la relatividad general, ie es el número imaginario de la relatividad especial, vorb es la velocidad orbital, v es la velocidad de la partícula y c es la velocidad de la luz en el vacío.
2. Desarrollo del Tema
Partiendo de la ecuación desarrollada de la energía cinética en el anterior trabajo “Sobre gravedad cuántica”:
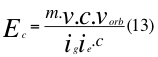
DondeEc es la energía cinética, m es la masa en reposo de la partícula,v es la velocidad de la partícula, vorb es la velocidad orbital, iges número imaginario de la relatividad general, ie es el número imaginario de la relatividad especial y c es la reconocida velocidad de la luz en el vacío.
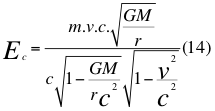
Donde Ec es la energía cinética, m es la masa en reposo de la partícula, v es la velocidad de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la reconocida velocidad de la luz en el vacío.
A esta anterior relación número catorce (14) de la energía cinética, le vamos a simplificar la velocidad de la luz y nos quedaría de la siguiente manera:
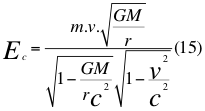
Donde Ec es la energía cinética, m es la masa en reposo de la partícula, v es la velocidad de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la reconocida velocidad de la luz en el vacío.
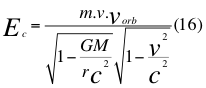
Donde Ec es la energía cinética, m es la masa en reposo de la partícula, v es la velocidad de la partícula, vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la reconocida velocidad de la luz en el vacío.
A esa velocidad (v) de cualquier objeto presente en la anterior ecuación de la energía cinética debemos buscarle una relación con las velocidades orbitales (vorb) de un campo gravitatorio. Comenzamos con Kepler:
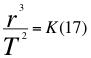
Donde r es la distancia radial hasta el centro del cuerpo másico central, T es el periodo y K es la constante de Kepler.
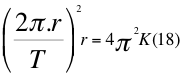
Donde π es una constante geométrica, r es la distancia radial hasta el centro del cuerpo másico central, T es el periodo y K es la constante de Kepler.
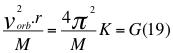
Donde vorb es la velocidad orbital, r es la distancia radial hasta el centro del cuerpo másico central, M es la masa del cuerpo másico central, π es una constante geométrica, K es la constante de Kepler y G es la constante de gravitación universal.
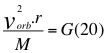
Donde vorb es la velocidad orbital, r es la distancia radial hasta el centro del cuerpo másico central, M es la masa del cuerpo másico central y G es la constante de gravitación universal.
![]()
Donde vorb es la velocidad orbital, r es la distancia radial hasta el centro del cuerpo másico central, G es la constante de gravitación universal y M es la masa del cuerpo másico central.
![]()
Donde vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico central.
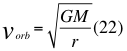
Donde vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico central.
Para que no varíe la igualdad en esta anterior ecuación número veinte y dos (22) a ambos miembros, los multiplicamos por un factor x positivo adimensional de la siguiente manera:
![]()
Donde x es el factor positivo adimensional, vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico central.
Le sacamos raíz cuadrada a ambos miembros de la igualdad anterior número veinte y tres (23) descrita:
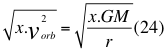
Donde x es el factor positivo adimensional, vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico central.
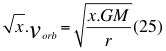
Donde x es el factor positivo adimensional, vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico central.
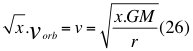
Donde x es el factor positivo adimensional, vorb es la velocidad orbital, v es la velocidad de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico central.
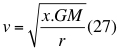
Donde v es la velocidad de la partícula, x es el factor positivo adimensional, G es la constante de gravitación universal, M es la masa del cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico central.
![]()
Donde v es la velocidad de la partícula, x es el factor positivo adimensional, G es la constante de gravitación universal, M es la masa del cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico central.
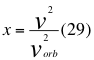
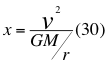
Donde x es un factor o índice adimensional que resulta de la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, v es la velocidad de la partícula, vorb es la velocidad orbital en el punto donde se encuentra la partícula en movimiento dentro del campo gravitatorio, G es la constante gravitacional, M es la masa del cuerpo másico y r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico central.
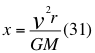
Donde x es un factor o índice adimensional que resulta de la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, v es la velocidad de la partícula, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico, G es la constante de gravitación universal y M es la masa del cuerpo másico o planeta.
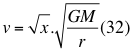
Donde v es la velocidad de la partícula, x es un factor o índice adimensional que resulta de la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta y r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico.
Si la anterior relación lineal de la velocidad (v) número treinta y dos (32) la reemplazamos en la también anterior relación de la energía cinética número catorce (14), nos queda la siguiente ecuación número treinta y tres (33):
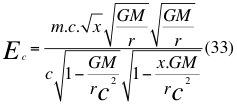
Donde Ec es la energía cinética, m es la masa en reposo de la partícula, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula hasta el centro del planeta o cuerpo másico y c es la reconocida velocidad de la luz en el vacío.

Donde Ec es la energía cinética, m es la masa en reposo de la partícula, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula hasta el centro del planeta o cuerpo másico y c es la reconocida velocidad de la luz en el vacío.
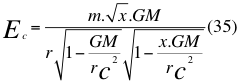
Donde Ec es la energía cinética, m es la masa en reposo de la partícula, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula hasta el centro del planeta o cuerpo másico y c es la reconocida velocidad de la luz en el vacío.
En esta anterior ecuación número treinta y cinco (35), debido a las bajas derivaciones sobre el tiempo ocasionado por las contracciones a esas minúsculas velocidades orbitales y de los objetos, podemos despreciar los efectos en dichas dilataciones del tiempo por dichas contracciones allí presentes en el denominador de la relación y nos quedaría entonces la energía cinética de la siguiente manera:
![]()
Donde Ec es la energía cinética, m es la masa en reposo de la partícula, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta y r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico.
Se puede observar que la energía cinética de una partícula que se mueva dentro de un campo gravitatorio, depende tanto de la posición que tenga el objeto en el interior del campo gravitacional, como de los valores que pueda tomar x. Si por ejemplo x tuviera el valor de cero, entonces la velocidad de cualquier partícula sería cero a cualquier altura, igualmente le sucedería a la energía cinética total de dicha partícula. Pero notemos que cuando x toma el valor de la unidad (1), entonces la velocidad de dicha partícula es igual a su primera velocidad cósmica y su energía cinética es la siguiente:
![]()
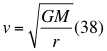
Donde x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula y el cuadrado de la velocidad orbital, v es la velocidad de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planetay r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la velocidad de la luz en el vacío.
![]()
Donde Ec es la energía cinética, m es la masa en reposo de la partícula, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula y el cuadrado de la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta y r es la distancia radial desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico.
Si x sigue aumentando su cuantía y llega hasta el valor de otro número entero como el dos (2) para el valor de x, aparece la configuración de la segunda velocidad cósmica o velocidad de escape y vemos que la relación treinta y dos (32) quede de la siguiente manera:
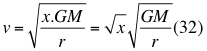
Donde v es la velocidad de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula y el cuadrado de la velocidad orbital y r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico.
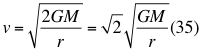
Donde v es la velocidad de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta y r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico.
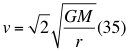
Donde v es la velocidad de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta y r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico.
Como vemos x puede tomar valores que van desde cero hasta valores configurados para cumplir la proporción de la segunda velocidad cósmica o velocidad de escape cuando x vale dos (2) o seguir aumentado hasta que la velocidad (v) sea igual a la velocidad de la luz en el vacío:
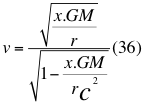
Donde v es la velocidad de la partícula, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula y el cuadrado de la velocidad orbital, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la velocidad de la luz en el vacío.
Se puede observar que en un agujero negro, como la velocidad para escape de la singularidad es igual a la velocidad de la luz, entonces a la primera velocidad cósmica de un agujero negro por efectos de la dilatación del tiempo por velocidad, se convierte en la velocidad de escape:
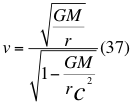
Donde v es la velocidad de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la velocidad de la luz en el vacío.
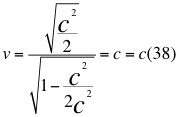
Donde v es la velocidad de la partícula y c es la velocidad de la luz en el vacío.
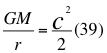
Donde G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la velocidad de la luz en el vacío.
3. Conclusiones
a)- LA PRIMERA GRAN CONCLUSIÓN es la primera velocidad cósmica de un agujero negro:
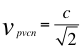
Donde vpvcn es la primera velocidad cósmica de un agujero negro, c es la velocidad de la luz en el vacío.
a)- LA SEGUNDA GRAN CONCLUSIÓN es la relación que define a la velocidad de cualquier objeto con respecto a la velocidad orbital dentro de un campo gravitatorio:
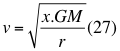
Donde v es la velocidad de la partícula, xes un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula y el cuadrado de la velocidad orbital, G es la constante de gravitación universal, Mes la masa del cuerpo másico o planetay r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico.
Vemos que aunque un objeto se eleve en altura sobre la superficie de un cuerpo másico a una velocidad constante, x continuará incrementándose al compas de dicha altura en el radio de la órbita.
b)- OTRA TERCERA GRAN CONCLUSIÓN es la expresión que define a x.
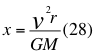
Donde x es un factor o índice adimensional que resulta de la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, v es la velocidad de la partícula, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico, G es la constante de gravitación universal y M es la masa del cuerpo másico o planeta.
![]()
Donde v es la velocidad de la partícula, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico, x es un factor o índice adimensional que resulta de la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, G es la constante de gravitación universal y M es la masa del cuerpo másico o planeta.
Vemos que aunque la velocidad continúe constante, sin embargo x seguirá aumentando indefectiblemente al compas del decremento de la velocidad orbital.
c)- OTRA CUARTA GRAN CONCLUSIÓN es la relación que define a la energía cinética como vector:
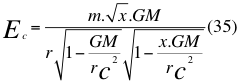
Donde Ec es la energía cinética en la gravedad cuántica, m es la masa en reposo de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula hasta el centro del planeta o cuerpo másico, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital y c es la reconocida velocidad de la luz en el vacío.
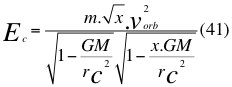
Donde Ec es la energía cinética en la gravedad cuántica, m es la masa en reposo de la partícula, x es un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula con el cuadrado de la velocidad orbital, vorb es la velocidad orbital de la partícula, G es la constante de gravitación universal, M es la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula hasta el centro del planeta o cuerpo másico y c es la reconocida velocidad de la luz en el vacío.
d)- OTRA QUINTA GRAN CONCLUSIÓN sería la cantidad de movimiento en la Gravedad cuántica:
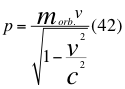
Donde p es la cantidad de movimiento en la gravedad cuántica, morb es la denominada por nosotros como masa orbital y c es la velocidad de la luz en el vacío.
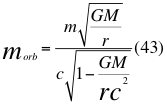
Donde morb es la denominada por nosotros como masa orbital, m es la masa en reposo del objeto, G es la constante de gravitación universal, Mes la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la velocidad de la luz en el vacío.
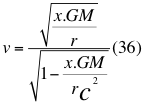
Donde v es la velocidad de la partícula, xes un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula y el cuadrado de la velocidad orbital, G es la constante de gravitación universal, Mes la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la velocidad de la luz en el vacío.
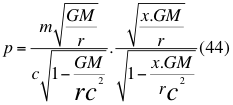
Donde p es la cantidad de movimiento en la gravedad cuántica, m es la masa en reposo del objeto, G es la constante de gravitación universal, Mes la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico, xes un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula y el cuadrado de la velocidad orbital y c es la velocidad de la luz en el vacío.
![]()
Donde Ec es la energía cinética, p es la cantidad de movimiento en la gravedad cuántica y c es la velocidad de la luz en el vacío
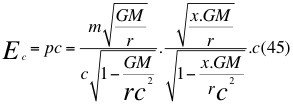
Donde Ec es la energía cinética, p es la cantidad de movimiento en la gravedad cuántica, m es la masa en reposo del objeto, G es la constante de gravitación universal, Mes la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico, xes un factor o índice adimensional que determina la relación entre el cuadrado de la velocidad de la partícula y el cuadrado de la velocidad orbital y c es la velocidad de la luz en el vacío.
e)- LA SEXTA y ULTIMA GRAN CONCLUSIÓN sería la cantidad de movimiento pero solo en la relatividad general:
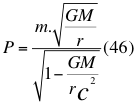
Donde P es la cantidad de movimiento en la relatividad general, m es la masa en reposo de la partícula, G es la constante de gravitación universal, Mes la masa del cuerpo másico o planeta, r es la distancia radial que hay desde el punto donde se encuentra la partícula en movimiento hasta el centro del planeta o cuerpo másico y c es la velocidad de la luz en el vacío.
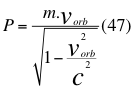
Donde P es la cantidad de movimiento en la relatividad general, m es la masa en reposo, vorb es la velocidad orbital y c es la velocidad de la luz en el vacío.
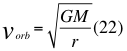
Donde vorb es la velocidad orbital, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central y r es la distancia radial hasta el centro del cuerpo másico.
4. Referencias de este artículo
[1] Sobre Gravedad cuántica
[1] 1Wikipedia, enciclopedia libre, Electrón agujero negro
[2] Gravedad cuántica y Coulomb
[3] Micro agujeros negros
[4] El tiempo propio es igual a período propio
[5] La velocidad de escape y el período propio
[6] La masa aparente es un Doppler de la masa invariante
[7] Ondas gravitacionales y los agujeros negros
[8] corrimiento al rojo gravitacional
[9] efecto Doppler relativista
[10] corrimiento al rojo
[11] corrimiento al rojo gravitacional
[12] efecto doppler relativista
[12] efecto doppler relativista
[13] efecto doppler relativista
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.
heberpico@hotmail.com