Resumen
En este trabajo se encuentra una relación global de la energía momento que involucra respectivamente a la relación energía momento de la relatividad general y a la relación energía momento de la relatividad especial, situación esta que necesita la presencia al mismo tiempo de cinco dimensiones entre ellas sorpresivamente hay dos variables de tiempo que lucen en sentidos contrarios, quienes serían el tiempo de la relatividad general y el tiempo de la relatividad especial, coexistiendo además estas variables con las tres dimensiones espaciales en el espacio-tiempo de la relatividad especial. Se encuentra así una explicación del por qué la relatividad especial, no ha podido reconocerles magnitudes vectoriales a la energía, aunque si lo hace de manera suficiente con la cantidad de movimiento. Este trabajo fundamenta razonadamente una duda de aquella noción física empírica quien sostiene que el modo correcto para calcular la energía cinética de un sistema, depende de su tamaño y la velocidad de las partículas que lo forman.
Palabras claves: Relación energía momento, Gravedad cuántica.
Abstract
This work is a global relationship of energy time correlation involving respectively the relationship energy of general relativity and the relationship time energy time of special relativity, this situation that needs the presence at the same time of five dimensions including surprisingly there are two variables of time on senses opposites, who would be the time of general relativity and special relativity timecoexisting in addition these variables with the three spatial dimensions in spacetime of special relativity. It is thus an explanation of the why special relativity, not has been able to recognize them vector quantities energy, although doing so sufficiently with the amount of movement. This work reasonably based a doubt of that empirical physical notion who argues that the correct way to calculate the kinetic energy of a system depends on its size and the speed of the particles that form.
Keywords: Energy time relationship, quantum gravity.
1. Introducción
En esta corta introducción vamos a hacer una referencia rápida de los puntos admitidos por la academia de manera indiscutible, que además son interesantes y claves en este artículo. Alguno de ellos son tratados en la relación energía momento de la relatividad especial, ítems que están totalmente aceptados en la comunidad científica con respecto a este tema desarrollado, todo según lo indica la enciclopedia libre de Wikipedia en un artículo identificado como relación energía momento.
Textualmente la enciclopedia libre de Wikipedia en cuanto a este tema dice lo siguiente “En la relatividad especial la relación de energía momento es la ecuación que relaciona las componentes del vector energía momento con la masa en reposo. La ecuación es la siguiente”:
![]()
Donde E es la energía total de la partícula en movimiento, m es la masa en reposo de la partícula, p es el momento lineal de la partícula y c es la velocidad de la luz en el vacío.
Siguiendo la anterior ecuación y definiendo a cada una de los variables de la energía, la cantidad de movimiento y la masa en reposos nos quedaría a continuación la siguiente relación:
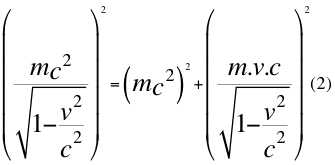
Donde m es la masa en reposo de la partícula, v es la velocidad relativa de la partícula con respecto a ese observador y c es la velocidad de la luz en el vacío.
Detallamos en las siguientes relaciones como está aceptado en la comunidad científica a cada una de las variables como son: la energía total de la partícula que se mueve quien significa la energía del cuarto vector del tiempo en el espacio-tiempo, la cantidad de movimiento que multiplicada por la velocidad de la luz representa la energía de los tres vectores restantes del espacio-tiempo y la energía de la masa en reposo relativo a ese mismo observador:
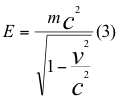
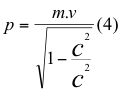
Donde E es la energía total de la partícula o mismo cuarto vector del tiempo en el respectivo espacio-tiempo plano de la relatividad especial, m es la masa en reposo de la partícula, p es la cantidad de movimiento de la partícula, v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
![]()
Donde Er es la energía en reposo de la respectiva partícula, m es la masa en reposo de la partícula y c es la velocidad de la luz en el vacío.
Notas: 1 Wikipedia, relación energía momento1
2. Desarrollo del Tema
El espacio-tiempo plano de la relatividad especial describe cómo una partícula, forma a cubos perfectos en el espacio-tiempo, que tienen la misma dirección y la misma arista del poliedro regular en la siguiente relación:
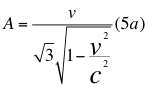
Donde A es la longitud de la arista del cubo formado en el espacio-tiempo, v es la diagonal del cubo formado en el espacio-tiempo y c es la velocidad de la luz en el vacío.
Como esos cubos perfectos que se describen en el espacio-tiempo de la relatividad especial son constantes en la dirección y el volumen, por eso es que Einstein insistía en que la relatividad especial, estaba diseñada solo para describir movimientos inerciales pero sin embargo, en movimientos uniformemente acelerados, cuando se iría describiendo regularmente en el espacio-tiempo a cubos y direcciones diferentes, también se puede aplicar la relatividad especial a esos movimientos. Lo que sí se puede decir es con seguridad es que la relatividad especial, solo se puede utilizar para describir el progreso en los movimientos utilizando el cambio de volúmenes cúbicos y no volúmenes esféricos como lo hace la relatividad general.
Tomamos entonces a la anterior relación energía momento de la relatividad especial como la siguiente ecuación:
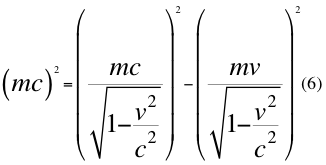
Donde m es la masa en reposo de la partícula, v es la velocidad relativa de la partícula, c es la velocidad de la luz en el vacío.
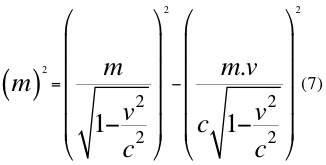
Donde m es la masa en reposo de la partícula, v es la velocidad relativa de la partícula y c es la velocidad de la luz en el vacío.
Esta anterior ecuación nos determina que en el espacio-tiempo de la relatividad especial a la masa, a pesar de ingresar a la ecuación como un simple escalar, también le corresponde distribuirse complementariamente para hacer presencia en los cuatro vectores sin romper la relación, en todo el espacio para que además utilice y sienta fielmente en el caso a la curvatura del espacio-tiempo.
Por eso es que hablando de cuadrivectores, cuadrivelocidad, cuadrimomento también corresponde incluir a la cuadrienergía y a la cuadrimasa como tales, lo que nos conlleva a decir que la siguiente relación número siete a (7a) es el cuarto vector del espacio-tiempo con respecto a la cuadrimasa en la relatividad especial, y la relación número siete b (7b) son los tres vectores restantes del espacio-tiempo con respecto a la misma cuadrimasa:
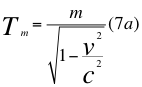
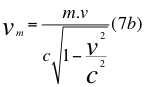
Donde Tm es el cuarto vector del tiempo del espacio-tiempo plano de la relatividad especial con respecto a la masa en reposo de la partícula, v es la velocidad relativa de la partícula, m es la masa en reposo de la partícula, vm son los tres vectores en el espacio-tiempo plano de la relatividad especial de la masa de la partícula y c es la velocidad de la luz en el vacío.
Aplicando el principio de equivalencia quien supone que un sistema, que se encuentra en caída libre y otro que se mueve en una región del espacio-tiempo sin gravedad, se encuentran en un estado sustancialmente similar, pues ambos casos se tratan de sistemas inerciales. Cualquier cuerpo que se mueva sin restricciones por un campo gravitatorio puede ser considerado como un sistema inercial, como es el caso de la caída libre y la de los planetas y satélites naturales alrededor de ellos.
La velocidad orbital es un movimiento inercial geodésico que indica el grado de curvatura en reposo que tiene el espacio-tiempo en cierto sitio de un determinado campo gravitatorio, ocasionado esto por una masa central.
Queremos abordar el espacio-tiempo curvo de la relatividad general sin tener que forzosamente limitarlo a una variedad pseudoriemanniana. Para esto utilizamos la misma estrategia que hace la relatividad especial pero utilizando esta vez a volúmenes no cúbicos en el espacio-tiempo, tal como lo ha hecho originalmente la teoría restringida, sino que aprovecharemos por un lado a la existencia en volumen de la constante de gravitación universal para obtener la velocidad instantánea en el tiempo y a la vez describir a las cantidades de volúmenes esféricos, correspondientes al conjunto de la masa central de un cuerpo en el espacio-tiempo dependiente totalmente de sus respectivos radios e igual que en la relatividad especial, aprovechando nuevamente a la constante acelerada de la gravitación universal, se pueda usar de nuevo muy bien para el cambio de volúmenes por la masa central uniformemente acelerados:
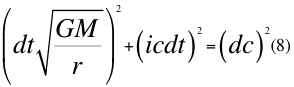
Donde dc es el diferencial del espacio que le corresponde a la velocidad de la luz, dt es el diferencial del tiempo, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central, i es la unidad imaginaria, r es la distancia radial desde el centro del cuerpo másico y c es la velocidad de la luz en el vacío.
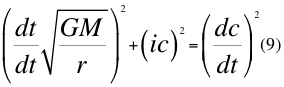
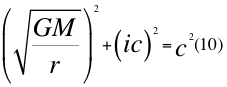
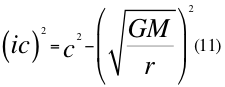
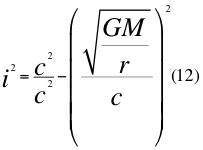
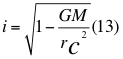
Donde i es la unidad imaginaria, G es la constante de gravitación universal, M es la masa del cuerpo másico central o planeta, r es la distancia radial desde un punto cualquiera del campo gravitatorio hasta el centro del planeta o cuerpo másico central y c es la velocidad de la luz en el vacío.
Tomando la anterior relación número once (11) de la cuadrivelocidad en la relatividad general, obtenemos la siguiente relación numero catorce (14):
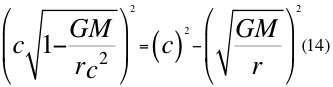
Donde G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico, r es el radio orbital o distancia radial que hay desde la partícula hasta el centro del cuerpo másico o planeta y c es la velocidad de la luz en el vacío.
Si multiplicamos a la anterior relación por la masa en reposo que tendría una partícula común fuera del campo gravitatorio, tomando por tanto a esa masa de dicho cuerpo como un simple escalar de una partícula cualquiera, nos queda la siguiente relación dl cuadrimomento:
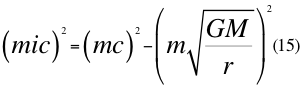
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, i es un número imaginario, G es la constante de gravitación universal, M es la masa del cuerpo másico central o planeta, r es la distancia radial desde la partícula hasta el centro del planeta o cuerpo másico central y c es la velocidad de la luz en el vacío.
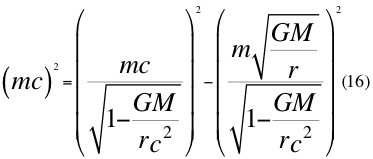
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico, r es el radio orbital o distancia radial que hay desde la partícula hasta el centro del cuerpo másico o planeta y c es la velocidad de la luz en el vacío.
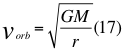
Donde vorb es la velocidad orbital de la partícula si está dentro del campo gravitacional, M es la masa del planeta o cuerpo másico, G es la constante de gravitación universal y r es el radio orbital o distancia radial que hay desde la partícula hasta el centro del planeta o cuerpo másico central.
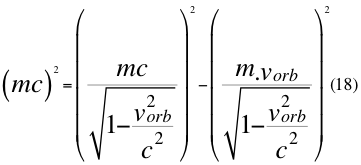
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, vorb es la velocidad orbital de la partícula si está dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
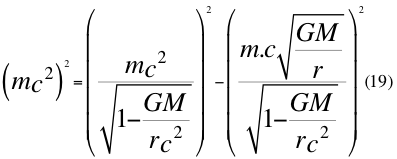
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central, r es el radio orbital o distancia radial que hay desde la partícula hasta el centro del cuerpo másico o planeta y c es la velocidad de la luz en el vacío.
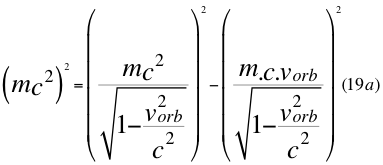
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, vorb es la velocidad orbital de la partícula si está dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
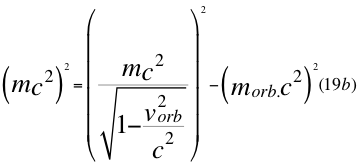
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, vorb es la velocidad orbital de la partícula si está dentro del campo gravitacional, morb es la masa orbital de la partícula cuando se encuentra dentro del campo gravitatorio y c es la velocidad de la luz en el vacío.
Ahora tomamos el equivalente del cuadrado de la velocidad orbital en las anteriores ecuaciones número diez y seis (16) y diez y siete (17) de la siguiente manera:
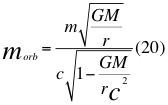
Donde morb es la masa en reposo relativo orbital de la partícula cuando ya está ubicada por dentro del campo gravitacional, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula,, G es la reconocida constante de gravitación universal, M es la masa del planeta o cuerpo másico, r es el radio orbital o distancia radial que hay desde la partícula hasta el centro del cuerpo másico o planeta y c es la velocidad de la luz en el vacío.
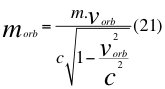
Donde morb es la masa en reposo relativo orbital de la partícula cuando ya está inmersa en reposo orbital por dentro del campo gravitatorio, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, vorb es la velocidad orbital de la partícula en reposo orbital dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
Asumiendo que la masa útil en la relatividad especial dentro de un campo gravitatorio no sería aquella masa en reposo que estaría ubicada fuera del campo gravitacional, sino se trataría de la masa inercial en reposo orbital ya modificada por el cuarto vector del tiempo en el campo gravitacional como una masa geodésica orbital, es una masa que ya no está en reposo porque se encuentra inmersa dentro de un campo gravitatorio cualquiera entonces, el último miembro del extremo derecho de la anterior ecuación de la relatividad general números diez y nueve b (19b), ese miembro del extremo derecho en la ecuación es la energía cinética de la partícula inmersa en el campo gravitatorio y es a ese miembro a quien se le puede aplicar la relación energía momento de la relatividad especial de la siguiente manera:
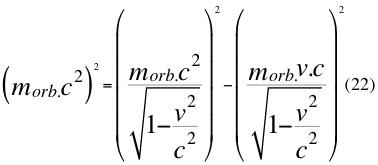
Donde morb es la masa en reposo relativo orbital de la partícula cuando ya está ubicada en reposo orbital por dentro del campo gravitatorio, v es la velocidad relativa de la partícula dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
Dividimos por la velocidad de la luz a la anterior relación número veinte y dos y nos queda la relación de la siguiente manera:
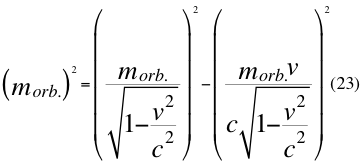
Donde morb es la masa en reposo relativo orbital de la partícula cuando ya está ubicada en reposo orbital dentro del campo gravitatorio, v es la velocidad relativa de la partícula dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
La anterior ecuación nos lleva a encontrar a la cantidad de movimiento como vector de la siguiente manera:
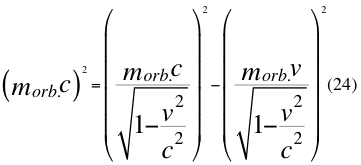
Donde morb es la masa en reposo relativo orbital de la partícula cuando ya está ubicada en reposo orbital dentro del campo gravitatorio, v es la velocidad relativa de la partícula dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
Como vemos la energía cinética que sería el miembro del extremo derecho de la anterior ecuación número veinte y dos (22), quien representa a los tres vectores del espacio-tiempo, y estaría al lado de la energía total del movimiento de la partícula quien significa el cuarto vector del tiempo y la relación de la energía en reposo orbital quedaría de la siguiente manera:
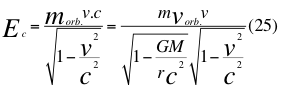
Donde Ec es la energía cinética relativa de la partícula en su movimiento relativo, morb es la masa en reposo relativo orbital de la partícula pero cuando ya está ubicada en reposo orbital dentro del campo, vorb es la velocidad orbital de la partícula si está dentro del campo gravitacional, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, v es la velocidad relativa de la partícula dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
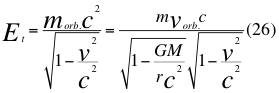
Donde Et es la energía total relativa de la partícula en su movimiento relativo o cuarto vector del tiempo en el espacio-tiempo, morb es la masa en reposo orbital de la partícula pero cuando ya está ubicada en reposo orbital dentro del campo gravitatorio, vorb es la velocidad orbital de la partícula si está dentro del campo gravitacional, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, v es la velocidad relativa de la partícula dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
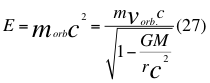
Donde E es la energía de la partícula cuando se encuentra en reposo relativo, morb es la masa en reposo orbital de la partícula cuando ya está ubicada en reposo orbital dentro del campo gravitatorio, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, vorb es la velocidad orbital de la partícula si está dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
Estas anteriores ecuaciones nos llevan a presentar a las diferentes clases de energía en el movimiento de las partículas:
![]()
Donde E es la energía en reposo relativo inercial de una partícula, Et es la energía total relativa del movimiento relativo de la partícula o cuarto vector del espacio-tiempo, Ec es la energía cinética relativa originada por el movimiento relativo de la partícula o los tres vectores del espacio-tiempo.
Tal como se puede observar a la energía cinética remplazando a la masa orbital de la ecuación número veinte y uno (21) en la ecuación número veinte y cuatro (24), nos queda entonces la energía cinética de la siguiente manera:
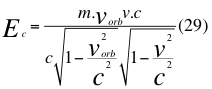
Donde Ec es la energía cinética relativa de la partícula originada por el movimiento relativo de la misma partícula, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, vorb es la velocidad orbital de la partícula pero cuando ya está ubicada por dentro del campo gravitatorio, v es la velocidad relativa de la partícula dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
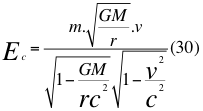
Donde Ec es la energía cinética relativa de la partícula originada por el movimiento relativo de la misma partícula, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central, v es la velocidad relativa de la partícula dentro del campo gravitacional, r es la distancia radial que hay desde la partícula hasta el centro del cuerpo másico central o planeta y c es la velocidad de la luz en el vacío.
Un cuerpo que tenga en la superficie de la tierra, una velocidad igual a la primera velocidad cósmica de 7,9 km/s, al cálculo entonces de la respectiva energía cinética de dicho cuerpo, se le puede aplicar la siguiente ecuación:
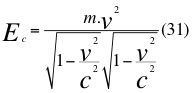
Donde Ec es la energía cinética relativa de la partícula originada por el movimiento relativo de la misma partícula, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central, v es la velocidad relativa de la partícula dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
3. Conclusiones
a)- Una GRAN CONCLUSIÓN es el hecho de haber encontrado la relación del cuadrimomento o cantidad de movimiento conservado en la relatividad general de una partícula que se mueve a lo largo de una geodésica:
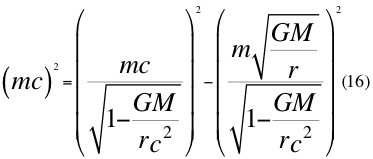
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico, r es el radio orbital o distancia radial que hay desde la geodésica de la partícula hasta el centro del cuerpo másico o planeta y c es la velocidad de la luz en el vacío.

Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, vorb es la velocidad orbital de la geodésica de la partícula si está dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
b)- Una GRAN CONCLUSIÓN es que en realidad la energía, es una magnitud física que cumple al igual que el momento lineal las condiciones de vectores, tienen módulo y dirección:
![]()
Donde Et es la energía relativa total o cuarto vector del tiempo en el movimiento relativo de una partícula, E es la energía de la partícula cuando está en el reposo relativo, Ec es la energía cinética relativa originada por el movimiento relativo de la partícula.
c)- Otra GRAN CONCLUSIÓN es el descubrimiento de la razón, del porque a pequeñas velocidades la energía cinética de la mecánica clásica, difiere tan asombrosamente con la energía cinética de la relatividad especial:

Donde Ec es la energía cinética relativa de la partícula originada por el movimiento relativo de la misma partícula, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central, v es la velocidad relativa de la partícula dentro del campo gravitacional, r es la distancia radial que hay desde la partícula hasta el centro del cuerpo másico central o planeta y c es la velocidad de la luz en el vacío.
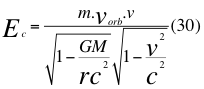
Donde Ec es la energía cinética relativa de la partícula originada por el movimiento relativo de la misma partícula, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central, v es la velocidad relativa de la partícula dentro del campo gravitacional, r es la distancia radial que hay desde la partícula hasta el centro del cuerpo másico central o planeta, vorb es la geodésica o velocidad orbital de la partícula pero cuando ya está ubicada por dentro del campo gravitatorio y c es la velocidad de la luz en el vacío.
d)- Otra GRAN CONCLUSIÓN es de que en este trabajo se demuestra de que la masa útil para la relación energía momento de la relatividad especial dentro de un campo gravitacional, no sería precisamente la masa invariante que sería la misma medida de la masa para todos los observadores inerciales o aquella masa propia en reposo que tiene una partícula fuera de cualquier campo gravitacional, pero por el contrario, si se aplica dentro de un campo gravitatorio le es suficiente con la respectiva masa en reposo pero, modificada por los efectos gravitacionales en el espacio-tiempo dentro del campo que se trabaja:

Donde morb es la masa en reposos relativo orbital de la partícula estando dentro del campo gravitacional, v es la velocidad relativa de la partícula dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
e)- Otra GRAN CONCLUSIÓN estaría en la identificación por este trabajo de la llamada por nosotros como la masa orbital:

Donde morb es la masa en reposo orbital de la partícula estando dentro del campo gravitacional, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la reconocida constante de gravitación universal, M es la masa del planeta o cuerpo másico, r es el radio orbital o distancia radial que hay desde la partícula hasta el centro del cuerpo másico o planeta y c es la velocidad de la luz en el vacío.
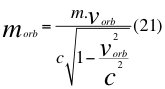
Donde morb es la masa en reposo orbital que le corresponde a la partícula en el campo gravitacional, m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, vorb es la velocidad orbital de la partícula estando dentro del campo gravitacional y c es la velocidad de la luz en el vacío.
f)- Otra GRAN CONCLUSIÓN es sobre la primera velocidad cósmica de un agujero negro, comenzamos diciendo que si el cuadrado de la velocidad de escape es igual al cuadrado de la velocidad de la luz en el vacío, entonces la primera velocidad cósmica de un agujero negro es la siguiente:
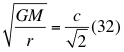
Donde G es la reconocida constante de gravitación universal, M es la masa del planeta o cuerpo másico, r es el radio orbital o distancia radial que hay desde la partícula hasta el centro del cuerpo másico o planeta y c es la velocidad de la luz en el vacío.
g)- Otra GRAN CONCLUSIÓN es la relación energía momento conjunta de la relatividad general y especial, donde se relacionan los tiempos de la relatividad general y especial (por no contar suficiente espacio):
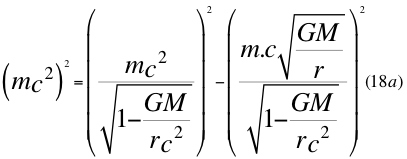
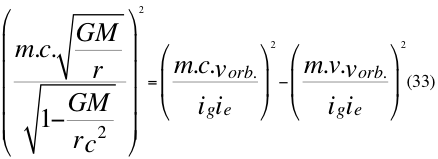
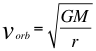
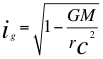
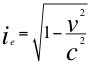
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central, v es la velocidad relativa de la partícula dentro del campo gravitacional, r es la distancia radial que hay desde la partícula hasta el centro del cuerpo másico central o planeta y c es la velocidad de la luz en el vacío.
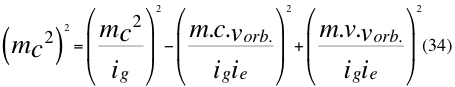
Donde m es la medida de la masa invariante que sería la misma para todos los observadores inerciales o masa propia en reposo de una partícula, G es la constante de gravitación universal, M es la masa del planeta o cuerpo másico central, v es la velocidad relativa de la partícula dentro del campo gravitacional, r es la distancia radial que hay desde la partícula hasta el centro del cuerpo másico central o planeta y c es la velocidad de la luz en el vacío.
Se puede ver que el cuarto vector del tiempo de la relatividad general y el cuarto vector del tiempo de la relatividad especial tienen sentidos contrarios e incluso en el fotón es mayor el de la relatividad especial.
También se puede observar en la anterior relación número treinta y cuatro (34), que los tres vectores involucrados en la energía cinética de la partícula, se encuentra enmascarada por tener aspecto de una probable cantidad de movimiento.
Analizando también a la relación número treinta y tres (33) se puede concluir que simplificando a ig y a vorb exactamente, nos queda sacrificando a las unidades de energía, a la anterior relación de cantidad de movimiento original número seis (6) de la relatividad especial, que en realidad no es una relación sino de energía.
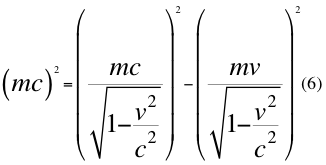
Donde m es la masa en reposo relativo de la partícula, v es la velocidad relativa de la partícula, c es la velocidad de la luz en el vacío.
4. Referencias de este artículo.
[1] Wikipedia, enciclopedia libre, relación energía momento1
[2] Gravedad cuántica y Coulomb
[3] Micro agujeros negros
[4] El tiempo propio es igual a período propio
[5] La velocidad de escape y el período propio
[6] La masa aparente es un Doppler de la masa invariante
[7] Ondas gravitacionales y los agujeros negros
[8] corrimiento al rojo gravitacional
[9] efecto Doppler relativista
[10] corrimiento al rojo
[11] corrimiento al rojo gravitacional
[12] efecto doppler relativista
[12] efecto doppler relativista
[13] efecto doppler relativista
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas médicos biofísicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.
heberpico@hotmail.com