El por qué de las dimensiones “extra”

Por Alejandro R. Álvarez Silva.

Es bien sabido que desde que apareció la Teoría de la Relatividad einsteniana, nos movemos en un mundo de cuatro dimensiones, a saber, las tres dimensiones espaciales (ancho, largo y alto, o bien x, y, z) y el tiempo considerado como una dimensión. Pero, ¿cuál es el verdadero rostro de esta dimensión?... ¿por qué ahora y no antes –de Einstein, se entiende- el tiempo es considerado como una magnitud insustituible en el campo físico?... Con anterioridad podía separarse nítidamente, por un lado el espacio (las tres coordenadas x, y, z), y por otro el tiempo.

Para un tiempo t determinado, el espacio (x, y, z) estaba también totalmente determinado para cualquier suceso o acontecimiento del mundo físico. De igual forma, en una “localización” prefijada (x, y, z), un suceso o acontecimiento se produce en el instante t de forma totalmente determinista. Y esto ocurría para cualquier observador, por supuesto, fuese cual fuese su estado de movimiento.

Ahora bien, tal obviedad fue sustancialmente cambiada al advenimiento de las llamadas “Ecuaciones de Lorentz”, que daban explicación o resolvían la aparente paradoja que surgía de la “experiencia de Michelson-Morley”, y se deducían u obtenían al traducir algebraicamente los dos principios de la Relatividad Restringida: 1. La luz se propaga con la misma velocidad c en todos los sistemas galileanos; 2. Los sistemas galileanos son equivalentes en el sentido de que existe una perfecta reciprocidad entre sus observaciones físicas.

En tales ecuaciones las relaciones entre las (x, t) y las (x´, t´) obtenidas por los observadores que se mueven uno con respecto a otro a la velocidad v (para acontecimientos que se producen a lo largo del eje de las x), son:

x´= (x-vt)/(1-v²/c²)^½

(1)

t´= (t-vx/c²)/(1-v²/c²)^½ (siendo c la velocidad de la luz en el vacío)

Ahora calculemos la expresión:

c² t´² –x´² De las expresiones anteriores (1), tendremos:

= c² (t-vx/c²)² (1-v²/c²) – (x-vt)²/(1-v²/c²)= (Haciendo operaciones)= c² t² – x² (2)

Vemos, pues, que la expresión s= c² t² –x² es un invariante que se llama “intervalo de universo” o “línea de mundo”.

Espacio y tiempo, según (1), son variables, pero la cantidad (2), compuesta por espacio y tiempo sí se conserva, lo que nos lleva a la posibilidad de contabilizar los sucesos o acontecimientos de nuestro universo físico relativista sobre esta magnitud invariante, “intervalo de universo”, que es la única que está ahora bien “determinada” para cualquier observador. (Ni el espacio ni el tiempo en este mundo relativista están ya determinados, pues aparecen “entrelazados” entre sí por las expresiones de Lorentz, según el movimiento relativo de cada observador).

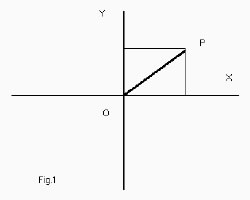
Tomando el espacio galileano con dos dimensiones (x, y) –fig. 1-, un acontecimiento acaecido en el punto P queda definido, para un observador S, por las coordenadas (x, y) y el instante t, para un observador situado en O. Ahora bien, para otro observador Σ que
se desplace con velocidad v respecto al observador S, situado también en O, el acontecimiento de P se producirá en las coordenadas (x´, y´) y el tiempo t´ definidos por (1), o sea, diferentes a los anteriores, así que la relatividad de los movimientos de los observadores S y Σ da al traste con la evidente “utilidad” que se obtenía con los sistemas de coordenadas galileanos en un mundo no relativista.

Todo nos conduce a buscar un “sistema de representación” de coordenadas que se “aproveche” de la anteriormente encontrada invariancia, es decir, del “intervalo de universo”.

Esa es la base para la introducción de una dimensión “imaginaria”, en una representación muy útil para la conservación del citado “intervalo de universo”.

Si en la fig. 1 sustituimos el eje y por el eje imaginario ict {i = (-1)^½}, tendremos la “representación de Minkowski” (fig. 2). (En esta representación se suele tomar la velocidad de la luz igual a la unidad).

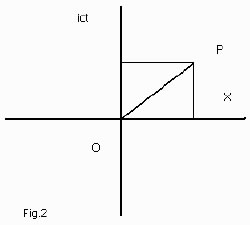
La distancia OP que en la fig. 1 era igual a x²+y², aquí será x²+i²c²t²= x²-c²t², y la distancia de P a O entonces c²t² –x², que es precisamente el “intervalo de universo”, distancia que es invariante sea cual sea el estado de movimiento del observador (S, Σ, etc.) situado en O.

Recapitulando: Las ecuaciones de Lorentz relativistas que nos señalan la variabilidad del espacio y el tiempo, nos indican la “conveniencia” práctica de introducir la unidad imaginaria temporal en un sistema de coordenadas llamado de Minkowski, muy útil para el encasillamiento de los sucesos o acontecimientos de nuestro universo espacio-temporal.

A continuación, describiremos la “representación de Minkowski” con un poco más detenimiento (fig. 3).

Sea un observador S. Se contará su tiempo sobre el eje ct, o paralelamente a él. (Además, como dijimos, se toma c=1). Consideremos uno sólo de los ejes de longitudes, x. El esquema permite explicar los acontecimientos de este universo lineal: cada acontecimiento, con sus coordenadas x y t, para dicho observador, está representado por un punto P. El punto O es el acontecimiento tomado como origen. Las rectas AOα y BOβ representan los desplazamientos de los rayos luminosos en este universo (x=ct). Los acontecimientos que se hallan a un intervalo de universo igual a la unidad, con respecto al acontecimiento O, pertenecen a las dos hipérbolas equiláteras trazadas:

c²t² –x²= ± 1

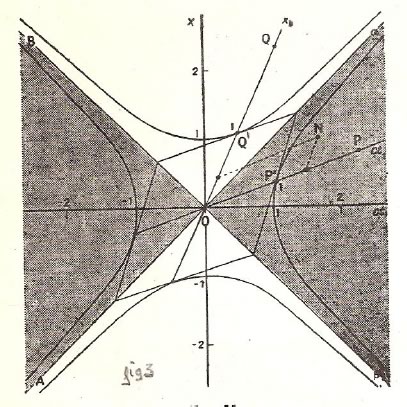
El intervalo entre los acontecimientos O y P se mide entonces por la razón OP/OP´.

En la superficie sombreada se tiene, para todo punto, que c² t² –x² >0.

Un observador Σ en movimiento con respecto a S, que tome ct₁ como eje de tiempos, con OP´ como unidad, debe tomar también x₁ (diámetro conjugado) como dirección espacial, con OQ´ como unidad, con el fin de mantener sin alteración el intervalo relativo a dos acontecimientos O y N. La pendiente de ct1 con respecto a ct define la velocidad de Σ con respecto a S; de otro modo, el ángulo (ct₁, ct) determina v/c.

Todo eje que atraviese la superficie sombreada puede tener un carácter temporal puro para un observador adecuado. Así, para el observador Σ, O y P se producen en el mismo lugar (x₁ =0) y el tiempo que los separa es el mínimo posible.

O y P no son simultáneos para ningún observador, puesto que P es siempre posterior a O. Todos los acontecimientos de αOβ son posteriores a O: es el cuadrante del futuro. De igual manera, todos los acontecimientos contenidos en AOB son anteriores a O, sea cual fuere el observador. La zona sombreada es la de los acontecimientos que pueden tener con O un lazo causal.

En cambio, todo eje (como OQ´x₁) que atraviese las zonas en blanco tiene un carácter espacial puro. Todo acontecimiento producido en esas zonas es tal que c² t² –x² <0. Para el observador Σ, cuya dirección espacial es x₁, Q es simultáneo con O. Pero puede haber observadores (eligiendo de forma arbitraria direcciones espaciales distintas de x1 en la zona clara) para los cuales Q sea anterior o posterior a O. No hay ningún nexo causal posible entre O y los acontecimientos de las zonas claras.

Observemos que, con respecto a los acontecimientos O y N, los observadores S y Σ descomponen el intervalo en espacio y en tiempo de manera distinta.

Y continuando con nuestro desarrollo de las dimensiones “extras”, advertir que la introducción del tiempo como cuarta dimensión en relatividad, no quiere decir que esta dimensión sea imaginaria (como podría suponerse cuando hablamos inicialmente de la representación de Minkowski), sino que su evidente realidad viene dada por las ecuaciones de Lorentz que son un resultado de la naturaleza, obtenido de la constancia de la luz para todos los observadores sea cual sea su estado de movimiento. Podríamos decir que la i imaginaria se introduce en la dimensión tiempo para transformar esta dimensión temporal en una espacial, y construir así “la distancia” llamada intervalo de universo. Este último invariante es lo que indirectamente nos indica la conveniencia de transformar (a través de la unidad imaginaria i) la dimensión tiempo en una dimensión espacial, iniciando así una progresión que continuará con la Relatividad General a una geometrización de la Física, de todo el espacio-tiempo que incluirá también dentro de sí toda la materia-energía.

Este tratamiento llevó a Kaluza en 1919 y posteriormente, en 1926 a Klein, a generalizar la teoría de la Relatividad, edificada sobre las cuatro dimensiones anteriores, usando un modelo geométrico en un espacio-tiempo de cinco dimensiones, es decir, introduciendo una dimensión más, lo que les permitió unificar gravitación y campo electromagnético.

Con estas cinco dimensiones Kaluza demostró que el “campo gravitatorio” de este universo pentadimensional se comporta exactamente como la gravedad conocida más el campo electromagnético de Maxwell, contemplado desde la perspectiva de las cuatro dimensiones. Según esto, no habría fuerzas en absoluto, sólo existe la cerrada geometría pentadimensional con partículas serpenteando a través de una estructurada “nada”.

Pero en los trabajos de Kaluza-Klein se considera a la quinta coordenada “compacta”, es decir, que está enrollada en un círculo muy pequeño con un radio del tamaño de la escala de Planck 10^-33cm. (La mínima distancia presumible del universo). Sería la dimensión tan pequeña que no podría verse, pero sí sus efectos.

En el espacio-tiempo de cinco dimensiones de Kaluza-Klein, el tensor métrico de dicho espacio-tiempo contiene la métrica cuatridimensional g_ij y el potencial vector Ai del campo electromagnético, además de las funciones escalares σ, φ:

           | gab + κ2 φ2 Aa Ab   κφ2 Aa |
  [ ĝAB] = | κφ2 Ab              φ2    |

A y B representan índices tensoriales que van de 0 a 4, y las minúsculas a, b,… índices tensoriales de 0 a 3. Así, las cinco coordenadas de un espacio-tiempo de Kaluza serían

⎨x^A⎬ = ⎨x^a, x⁴⎬ = ⎨ x⁰, x¹, x², x³, x⁴⎬, donde la coordenada 0-ésima es la coordenada temporal, la coordenada 4-ésima es la coordenada asociada a la quinta dimensión adicional, y las otras tres son las coordenadas espaciales ordinarias.

Como hemos dicho, Kaluza añade la llamada “condición cilíndrica” (compactación), que consiste en imponer que ninguna de las componentes del tensor pentadimensional ĝAB dependa de la coordenada adicional x4. Entonces las ecuaciones de campo serían las condiciones del Electromagnetismo clásico más las ecuaciones de la Relatividad General y una ecuación más para el campo escalar adicional:

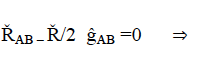
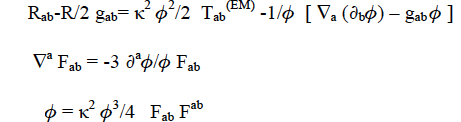
Dichas ecuaciones de los campos gravitatorio o eléctrico se generalizan con facilidad a otras dimensiones.

En un espacio de n dimensiones hay que tratar con una ley inversa de las potencias n-1. Por eso, en tres dimensiones, n-1=2, será la ley inversa del cuadrado. En cuatro dimensiones, n-1=3, será la ley inversa del cubo, y así para las demás dimensiones. Pero, en un espacio de más de tres dimensiones, por ejemplo, se demuestra que los satélites de un planeta trazarían una rápida espiral hacia él, siendo absorbidos, y lo mismo ocurriría con los átomos, así que la química, y la misma vida no serían posibles.

También la propagación de las ondas depende sensiblemente de las dimensiones. Con un espacio con un número par de dimensiones, existirían efectos de reverberación, con lo que la onda no se propagaría con nitidez, como ejemplo, la dificultad de transmitir señales bien definidas en una superficie de dos dimensiones como una lámina de caucho.

La compactación de la quinta dimensión significa que lo que se toma como un punto en el espacio tridimensional es en realidad un pequeño círculo entorno a otra dimensión del espacio. Desde cada punto del espacio parte un pequeñísimo bucle en una dirección que no es ni arriba, ni abajo, ni ninguna otra en el espacio “sentido” por nuestros sentidos (valga la redundancia).

La teoría de Kaluza-Klein quedó apartada de la ciencia con el descubrimiento de las fuerzas débil y fuerte, hasta finales de los años setenta, ya con las GTU o Teorías Unificadas y la Supergravedad.

La propiedad central de los campos de fuerza es la presencia de algunas simetrías abstractas, lo que da poder y elegancia. Esta presencia de simetrías sugiere algún tipo de geometría oculta. Precisamente en la teoría de Kaluza-Klein revitalizada, las simetrías del campo de gauge se vuelven concretas: son las simetrías geométricas que viven asociadas a las nuevas dimensiones espaciales.

Como en la idea central de Kaluza-Klein las fuerzas se acomodan introduciendo más dimensiones espaciales en el espacio-tiempo; como hay varias fuerzas para acomodar, ello requiere la introducción de varias dimensiones adicionales. El recuento del número de operaciones de simetría necesario para esa gran fuerza unificada requiere siete nuevas dimensiones: en total diez dimensiones, once con el tiempo. Por tanto, la versión moderna de la teoría de Kaluza-Klein postula un universo de once dimensiones.

Y de nuevo se supone que las siete dimensiones adicionales están “enrolladas” de modo que por su tamaño no se pueden percibir. La forma de enrollar una dimensión adicional es un círculo, pero hay muchas formas de “enrollar” espacios de más dimensiones. Con siete dimensiones el número de tipologías posibles es muy grande.

El análogo heptadimensional de una esfera es una heptaesfera. Cada punto del espacio tridimensional es una diminuta “hiperesfera” de siete dimensiones. La heptaesfera posee simetrías adicionales no encontradas en la esfera corriente. Con éstas se identifican las “simetrías de gauge” que subyacen en los campos de fuerza.

Sabemos que el modelo estándar (ME) de partículas unifica la fuerzas electromagnética, débil y fuerte, pero no las interacciones gravitacionales. La teoría de cuerdas es una candidata para unificar los efectos gravitacionales con las interacciones del ME de forma consistente a nivel cuántico. En esta teoría, los elementos básicos de la materia (leptones y quarks) dejan de ser definidos como partículas puntuales, pasando a ser descritos como objetos unidimensionales llamados cuerdas. En esta descripción, cada modo de vibración representa una partícula distinta.

Las distintas versiones de las teorías de cuerdas y supercuerdas son de hecho teorías de Kaluza-Klein en las que se han combinado principios de cuantización. Existen versiones de teoría de cuerdas de 0, 11 y 26 dimensiones. En la teoría de supercuerdas, además de la dimensión temporal y las tres dimensiones espaciales ordinarias, se conjetura que las direcciones adicionales podrían tener una topología de variedad de Calabi-Yau de seis dimensiones. (La variedad de Calabi-Yau es una variedad compacta que admite una métrica con curvatura de Ricci nula, es decir, es una variedad “plana”. En una variedad compleja, los únicos ejemplos son familias de toros –donuts-).
Las primeras teorías de cuerdas no contenían grados de libertad fermiónicos, por eso recibieron el nombre de cuerda bosónica, pero en 1984 Michael Green y John Schwartz, junto con otros autores, se dieron cuenta de que cuando se incorpora la supersimetría a la teoría de cuerdas, la Mecánica Cuántica no tiene problemas con los infinitos. A esta teoría se le denominó de supercuerdas y requirió un espacio- tiempo de 10 dimensiones para su formulación, de las que 6, como dijimos, están compactificadas de acuerdo con la hipótesis de Kaluza-Klein.

Pero, a finales de 1990 Joe Polchinski mostró que las teorías de cuerdas contienen, además, objetos extendidos: las DP-branas (siendo p las dimensiones espaciales, y D en honor a Dirichlet). Una 0-brana sería una partícula puntual que evoluciona según una “línea de mundo” (la extensión natural del “intervalo de universo”, visto con anterioridad); una 1-brana es la citada cuerda que evoluciona según la llamada “hoja de mundo” y una 2-brana es una membrana cuya evolución se llama “volumen de mundo”.

Petr Hovara y Edgard Witten consideraron teorías de cuerdas con dos 10-branas encajadas en un espacio-tiempo de 11 dimensiones. A bajas energías la gravedad se propaga en todo el espacio-tiempo multidimensional, mientras el resto de los campos se localiza en las branas. En particular, la localización de la materia a lo largo de la brana explica por qué la Física a bajas energías es efectivamente cuatro dimensional para todas las interacciones excepto la gravedad.

Existen diversos mecanismos para localizar los campos del ME (modelo estándar) en la brana; el más simple es considerar la gravedad de la brana, y también simetrías especiales en las dimensiones extra a las que se llama Orbifold, así como defectos topológicos (vórtices y tipo pared).

En el modelo RS se parte del uso de la tensión de la brana para producir gravedad, en presencia de una constante cosmológica. Las soluciones de las ecuaciones de Einstein, entonces, incorporan además condiciones de frontera apropiadas a la presencia de una o dos branas conocidas como condiciones de Israel. Es notable que puedan encontrarse unas soluciones que preservan la invariancia de Poincaré cuatro-dimensional. En este tipo de modelos las dimensiones extras no tienen límite de tamaño.

Los escenarios de dimensiones extras tienen implicaciones fenomenológicas en nuestro mundo cuatrodimensional, tales como desviaciones de la ley gravitacional de Newton para cuerpos masivos en la brana, el efecto Casimir o el corrimiento Lamb.

Para terminar haré hincapié en la importancia de la introducción de la unidad imaginaria i, en los cálculos realizados con las unidades extras, en particular en la cuarta dimensión (tiempo), como oportunamente vimos, para “asemejarla” a un espacio en la expresión del “intervalo de universo”, y también, y ya como número complejo (a,bi) insustituiblemente en el mundo cuántico, pues, por ejemplo, en los estados posibles abiertos al electrón, que se escriben como w|A〉 + z|B〉, los factores de peso w y z son números complejos, de los cuales al menos uno debe ser no nulo.

Pero esta aplicación del número imaginario i , con los complejos, no acaba aquí, sino que se generaliza con los llamados cuaterniones, extensión de los números reales, similar a la de los números complejos, añadiendo las unidades imaginarias i, j, k a los reales, con el operacional i²=j²=k²=i j k= -1.

Y los cuaterniones son importantísimos en física: en el electromagnetismo, la teoría de la relatividad, la mecánica cuántica, etc. También son muy usados en gráficos por computadora para representar la orientación de un objeto en un espacio tridimensional, etc.

Hamilton en 1843 descubrió los cuaterniones al intentar extender los números complejos a un número mayor de dimensiones.

La familia de todos los posibles estados de un sistema cuántico constituye lo que se conoce como espacio de Hilbert, y un espacio de Hilbert es un espacio vectorial complejo. Cada posición alternativa que puede tener la partícula cuenta como algo que aporta una dimensión independiente al espacio de Hilbert. El estado general que describe la posición cuántica de la partícula es una superposición con coeficientes complejos de todas estas diferentes posiciones individuales (la función de onda de la partícula).

Así, vemos que los números imaginarios son insustituibles en mecánica cuántica, en especial para el estudio de los estados de espín (momento angular o rotación) de las partículas.

Finalmente y resumiendo, ¿cuál es la aportación básica de la introducción de las dimensiones extra en nuestro mundo, en particular, en nuestra ciencia?... Pues, ha sido la “historia” de una “geometrización” progresiva de la física, que ha coadyuvado a un desarrollo matemático poderoso en las teorías de campo, relatividad, cuántica, teorías de cuerdas, branas, etc.

Pero, ya desde un punto de vista un tanto filosófico, no deberíamos pensar que realmente han “aparecido nuevas dimensiones” físicas palpables en nuestro universo cuatridimensional espacio-temporal… Las dimensiones “extras” son realmente un “artificio matemático” muy potente para explicar y cuantificar los fenómenos o acontecimientos, estos sí reales, que aparecen a nuestro alrededor, como: las masas de las partículas, los efectos electromagnéticos, gravitacionales, interferenciales, etc. Nuestro mundo real, “histórico”, basado en sucesos o acontecimientos, sigue siendo cuatridimensional (tres dimensiones espaciales y una temporal).

REFERENCIAS:

Las sombras de la mente, Roger Penrose (Crítica).

Los números imaginarios (A ciencia abierta. com).

Realidad y números imaginarios (Libro de notas. com).

“Cuaternión”, “Teoría de Kaluza-Klein”, “Variedad de Calabi-Yau” (Wikipedia).

Sobre las dimensiones extra espaciales (http://www.journal.lapen.org.mx).

Nuestro Universo, Alejandro Álvarez Silva. (Biblopia.com).

La Relatividad, Paul Couderc (Ed. Universitaria de Buenos Aires).