Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com
heberpico@telecom.com.co
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
La contracción de Lorentz ha sido altamente exitosa para contraer y dilatar relativamente a longitudes, tiempo, velocidad y hasta masa en la relatividad especial pero, pierde efectividad cuando se quiere preservar en figuras compuestas que presentan contracciones y dilataciones de Lorentz parcialmente superpuestas una sobre la otra, como es el caso del cuadrimomento y las energías deducidas a través de la cuadrimasa. Si usamos la masa como escalar la contracción de Lorentz es suficiente en el cuadrimomento pero, si la usamos como vector, la clásica contracción de Lorentz es inútil. Buscando hallar entonces una relación de energía momento que fuera apta para el estudio del movimiento de todo tipo de partículas, tras ello pues en este trabajo se encuentra sin contradicción, una relación de energía-momento provista de una más potente contracción diferente a la de Lorentz e identificada como “Cuadricontracción de Cuadri-Lorentz” totalmente útil para el estudio relativo de la energía y cuadrimomento que además resuelve el problema de usar sin explicaciones convincentes, a formulas matemáticas diferentes para el estudio de un mismo fenómeno como en la energía cinética y cantidad de movimiento entre otras.
Palabras claves: Energía Potencial, Energía Cinética, Cantidad de Movimiento, Cuadrimomento, Cuadrimasa, Cuadrivelocidad, Cuadrivector, Contracción de Lorentz, Cuadricontracción de Lorentz.
Abstract
The contraction of Lorentz has been highly successful to collapse and relatively dilate lengths, time, and speed and to mass in special relativity, but loses effectiveness when you want to preserve in composite figures featuring contractions and overlapping Lorentz dilatations one over the other, as it is the case of the cuadrimomento and energies deducted from the cuadrimasa. If we use the mass as scale contraction of Lorentz is sufficient in the cuadrimomento, but if you use it as a vector, the classical contraction of Lorentz is useless. Looking for then find a time that would be suitable for the study of the movement of all kinds of particles energy relationship, after that because this work is no contradiction, provided a more powerful contraction different from the Lorentz and identified as "Cuadricontracción de Cuadri-Lorentz" fully useful for the study of energy and cuadrimomento also resolves the problem of use without convincing explanations, energía-momento ratio to formulas different for the same phenomenon study as in kinetic energy and amount of movement including mathematics.
Key Words: Energy potential, energy kinetics, quantity movement, Cuadrimomento, Cuadrimasa, Cuadrivelocidad, Cuadrivector, Lorentz contraction, Lorentz Cuadricontracción.
1. Introducción
En esta introducción sin recurrir al lenguaje matemático de matrices ni tensores se logra deducir la misma clásica relación energía-momento de la relatividad especial, la presentamos en esta introducción como prueba de que no existe contradicción con el método utilizado para el objetivo de este trabajo, que es precisamente el de hallar un cuadrimomento a partir de la masa como cuadrivector cuadrimasa.
Un cuadrivector es la representación matemática en forma de vector de cuatro dimensiones de una magnitud vectorial en teoría de la relatividad. Los trabajos de Lorentz, Poincaré, Einstein y Minkowski sobre el electromagnetismo clásico llevaron a la idea de que no es posible definir un tiempo absoluto que transcurre de manera idéntica para todos los observadores con independencia de su estado de movimiento. La no existencia de un tiempo absoluto, requería que existiera una medida de tiempo para cada observador. Así el conjunto de eventos (puntos del espacio-tiempo) llevaban de manera natural a definir vectores de cuatro dimensiones:
![]() (1)
(1)
Donde E es el espacio vectorial y las cuatro componentes representando a las tres coordenadas espaciales del sitio en el cual ocurre algo, y el instante en que sucede. Pues c es simplemente la velocidad de la luz que aparece multiplicada por el tiempo propio del evento para traducir en espacio el tiempo relativo de un observador.
La relatividad especial usa tensores y cuadrivectores para representar un espacio pseudo-euclídeo. Este espacio, sin embargo, es similar al espacio euclídeo tridimensional en muchos aspectos y es relativamente fácil trabajar en él. El tensor métrico que da la distancia elemental (ds) en un espacio Euclídeo se define como:
![]() (2)
(2)
Donde dx, dy, dzson diferenciales de las tres coordenadas cartesianas espaciales y dses el diferencial resultante.
En la geometría de la relatividad especial, para mostrar el carácter pseudoeuclídeo de la geometría espacio-temporal, se añade una cuarta dimensión de luz contraída dada en el producto jcdt,donde t es el tiempo, cla velocidad de la luz y j la unidad de contracción. Siendo además consecuente con esa cuarta dimensión que se agrega en el planteo de este artículo, se le debe considerar siempre en sentido ortogonal a la dirección resultante de las tres coordenadas cartesianas espaciales. El cuadrivector resultante es la diferencial del espacio luz y queda el intervalo relativista, en forma diferencial, de la siguiente manera:
![]() (3)
(3)
Donde dces el diferencial del espacio luz o cuadrivector, dx, dy, dzson los diferenciales de las tres coordenadas cartesianas espaciales y jcdt es el cuarto vector añadido.
De la misma manera que la velocidad en mecánica newtoniana es la derivada temporal de la posición respecto al tiempo, en la teoría especial de la relatividad la cuadrivelocidad es la derivada temporal del cuadrivector posición respecto al tiempo propio de la partícula. La cuadrivelocidad es una magnitud vectorial asociada al movimiento de una partícula, usada en el contexto de la teoría de la relatividad, que es también tangente a la trayectoria de dicha partícula a través del espacio-tiempo cuatridimiensional. Por esto, partiendo de la anterior ecuación número tres (3) y trasladando términos equivalentes obtenemos la cuadrivelocidad de la siguiente manera:
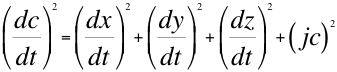 (4)
(4)
![]() (5)
(5)
En la anterior ecuación número cinco (5) de la cuadrivelocidad, se puede observar todavía el producto jc que aun resta y perdura justamente de la cuarta dimensión inicialmente añadida. Esa unidad jde contracción o coeficiente de contracción es precisamente el elemento matemático que aporta el substrato fijo de la relatividad general, que aparece de manera relacional entre dos acontecimientos del espacio tiempo ya que el vacío es dependiente de la trayectoria del observador en el espacio tiempo. Exactamente, jes igual al cociente de la relación entre dos tipos de masas en el movimiento de la misma partícula que se mueve con respecto a un observador además, esa misma unidad de contracción j, también es igual a la contracción de Lorentz tal como se describe en la siguiente relación:
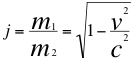 (6) m2 > m1
(6) m2 > m1
Donde jes el coeficiente de contracción, m1 es la masa menor y m2 es la masa de mayor tamaño en el movimiento de la partícula.
Podemos tomar a cualquiera de los dos valores equivalentes de jexpresados en la anterior relación seis (6) para remplazarlo en la ecuación número cinco (5) de este trabajo, ya sea que utilicemos la relación entre las masas o, tomemos la contracción de Lorentz como al parecer fue la opción y camino que siguieron los cálculos de Einstein tal como se expresa en las siguientes relaciones:
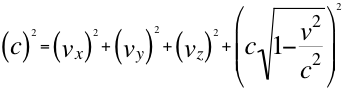 (7)
(7)
 (7)
(7)
Remplazando y trasladando matemáticamente la contracción de Lorentz en toda la ecuación, nos queda la anterior relación número siete de la siguiente manera:
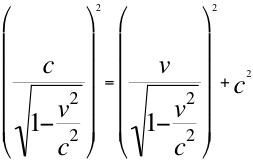 (8)
(8)
Aquí es el momento crucial cuando Einstein involucra la masa como un simple escalar a través de utilizar la misma definición de cantidad de movimiento de Newton, ya que toda la relación de cuadrivelocidad anterior es multiplicada por la misma masa escalar invariante m que deja la relación de la siguiente manera:
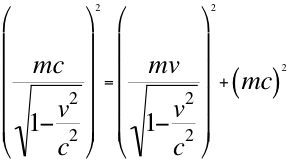 (9)
(9)
 (10)
(10)
Entonces Einstein distingue el concepto de masa relativista de la siguiente manera:
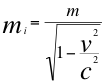 (11)
(11)
Donde mi es la masa relativista de Einstein, m es la masa invariante y de presente aparece en la relación once (11) la reconocida contracción de Lorentz.
![]() (12)
(12)
![]() (13)
(13)
Esta relación anterior nos conduce finalmente a la siguiente reconocida y famosa ecuación de la relatividad especial:
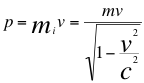 (14)
(14)
![]() (15)
(15)
Donde mi es la masa relativista para Einstein, m es la masa invariante, pes la cantidad de movimiento, v es la velocidad de la partícula, c es la velocidad de la luz y Ees una energía no invariante.
2. Desarrollo del Tema
Vamos a iniciar el desarrollo de este tema en este trabajo desde la ecuación número cinco (5), relación donde se encuentra el coeficiente de contracción j que su identidad la podemos remplazar según lo expresa la relación seis (6), ya sea por las respectivas masas que lo originan o por la conocida contracción de Lorentz:
![]() (5)
(5)
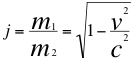 (6) m2 > m1
(6) m2 > m1
Si remplazamos a j por la contracción de Lorentz en la ecuación número cinco (5), nos resulta entonces de esa manera es la llamada relación de la cuadrivelocidad, expresada en la siguiente proporción:
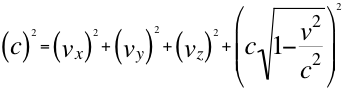 (16)
(16)
Pero si remplazamos a j por las respectivas masas que lo originan en la ecuación número cinco (5), nos resulta entonces de esa manera es la llamada relación de la cuadrimasa, formulada en las siguientes expresiones:
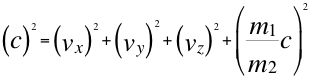 (17)
(17)
![]() (17)
(17)
![]() (17)
(17)
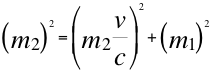 (18)
(18)
Esta anterior ecuación número dieciocho (18), es la que identificamos como cuadrimasa, que tiene involucradas a dos tipos de masas en el movimiento de la misma partícula y podemos darle el nombre cualquiera pero siempre deben respetar la relación entre ellas. Si una de ellas es la masa invariante, pues la otra es la gravitacional, pero lo contrario también podía ser. Así surge un tercer tipo de masa llamada masa inercial aparente.
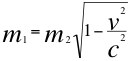 m2 > m1
m2 > m1
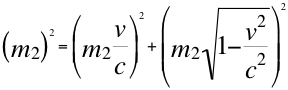 (19)
(19)
Hasta ahora podemos decir en el trabajo que contamos con la relación de la cuadrivelocidad en la ecuación número dieciséis (16) y la cuadrimasa en la ecuación número diecinueve (19), relaciones que presentamos de la siguiente manera:
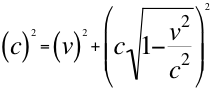 (16)
(16)
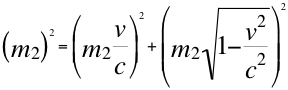 (19)
(19)
En la relación de la cuadrimasa o número diecinueve (19) vamos a asumir que m2 como única masa, es la masa invariante m de la partícula y nos queda la cuadrimasa de la siguiente manera:
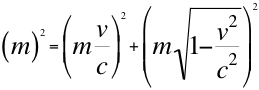 (19)
(19)
Vemos que en ambos cuadrivectores, nos referimos a la cuadrivelocidad y a la cuadrimasa, en ambos vectores sus componentes están expresados con respecto a la cabeza del respectivo vector resultante o cuadrivector resultante por ejemplo, la cuadrivelocidad está expresada con respecto a la velocidad de la luz y la cuadrimasa, igual con respecto a la masa invariante de la partícula. Veamos:
![]()
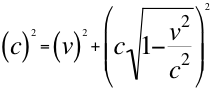 (16)
(16)
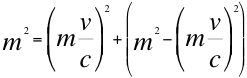 (19)
(19)
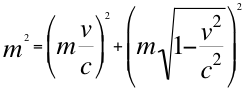
Igual podemos hacer para obtener el cuadrimomento resultante del producto escalar entre la cuadrivelocidad y la cuadrimasa, sobretodo teniendo en cuenta que el cuarto componente vectorial de la cuadrivelocidad y la cuadrimasa, presentan a la contracción de Lorentz, cuestión que obliga un cuadrimomento contraído doblemente por la contracción de Lorentz y necesita entonces una potente contracción resultante mas severa que la de Lorentz:
![]() (16)
(16)
![]() (19)
(19)
Nos quedaría el cuadrimomento de la siguiente manera:
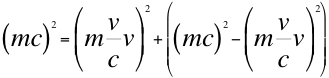 (20)
(20)
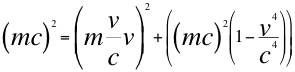 (21)
(21)
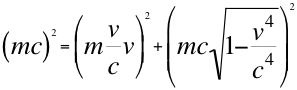 (22)
(22)
Si continuamos el desarrollo del tema y multiplicamos por la velocidad de la luz, a toda la anterior relación número veintidós (22), nos quedaría la relación de la energía-momento de la siguiente manera:
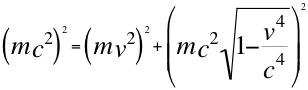 (23)
(23)
Identificando entonces las diferentes clases de energía como la energía total e invariante de la partícula, la energía cinética y la energía potencial en la anterior relación tenemos:
![]() (23)
(23)
Donde Et es la energía total e invariante de la partícula, Ec es la energía cinética de dicha partícula y Ep es la energía potencial.
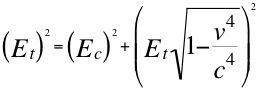 (23)
(23)
![]()
![]()
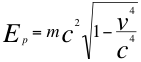
3. Conclusiones.
A)-La primera conclusión es la confirmación mediante este trabajo del carácter vectorial de la masa y con ello la deducción nuevamente de la energía cinética:
![]() (24)
(24)
mi es la masa inercial aparente, Ec es la energía cinética, m es la masa invariante, v es la velocidad de la partícula, p es la cantidad de movimiento y c la velocidad de la luz.
B)-La segunda conclusión es la nueva formulación matemática que resulta de esta manera para la energía Potencial:
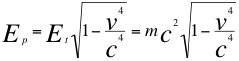 (25)
(25)
Donde Ep es la energía potencial, Et es la energía total, m es la masa invariante, v es la velocidad de la partícula y c la velocidad de la luz.
C)-La tercera conclusión es la presentación de la nueva formulación matemática de la cantidad de movimiento:
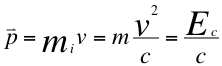
Donde mi es la masa inercial aparente, p es la Cantidad de movimiento, m es la masa invariante, v es la velocidad de la partícula y c es la velocidad de la luz.
D)-La cuarta conclusión es la nueva formulación de la masa inercial aparente que es directamente proporcional a la velocidad de los cuerpos:
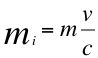
Donde mi es la masa inercial aparente y m es la masa invariante.
E)-La quinta conclusión es la representación en la ecuación relativista de las diferentes clases de energías involucradas en el movimiento de un cuerpo: Et es la energía total del movimiento de la partícula, Ec es la energía cinética de dicha partícula y Ep es la energía potencial que tiene el movimiento de la misma partícula:
![]()
F)-La 6º conclusión es para dejar identificada en la nueva Relación de energía-momento totalmente independiente de la contracción de Lorentz en la siguiente ecuación número veintitrés (23):
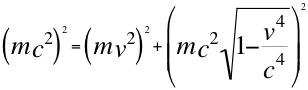 (23)
(23)
Donde m es la masa invariante, v es la velocidad de la partícula y c es la velocidad de la luz.
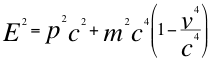 (23)
(23)
Donde E es la energía invariante equivalente a la masa invariante de la partícula, p la cantidad de movimiento, c la velocidad de la luz, m la masa invariante de la partícula.
G)-La séptima conclusión es sobre la ecuación veintitrés (23) de la relación de energía-momento de este trabajo, que también se puede presentar como la de Einstein de la siguiente manera:
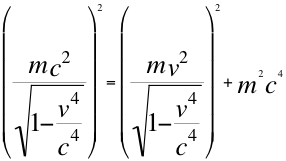 (23)
(23)
H)-La octava y última conclusión es la presentación a la comunidad académica, de la nueva contracción matemática que es quien realiza la contracción en el cuadrimomento, el mismo papel que hace la contracción de Lorentz en la respectiva cuadrivelocidad y cuadrimasa, identificada como “Cuadri-contracción de Cuadri-Lorentz” o sencillamente Cuadri-Lorentz:
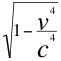
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
[15] http://www.monografias.com/trabajos-pdf2/matematicas-energia-cinetica-potencial-movimiento/matematicas-energia-cinetica-potencial-movimiento.pdf
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
[44] http://www.monografias.com/usuario/perfiles/pico_jimenez_heber_gabriel
[45] http://www.monografias.com/usuario/perfiles/pico_jimenez_heber_gabriel/monografias
[46] http://www.monografias.com/usuario/perfilprivado/monografias/
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.