Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com, heberpico@telecom.com.co
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
Debido al recóndito estudio de la profunda relación secreta que hay entre el objeto observado y el observador en la relatividad Especial, esto le permite a este trabajo que sin utilizar términos de matrices ni tensores, encuentre también cómo la materia crea gravedad, e inversamente, cómo la gravedad afecta concentrando en un punto a la materia. Aquí se consigue todo esto partiendo también precisamente de la constante de gravitación universal de Newton, tal como aquella fuerza que es determinante en el acoplamiento entre la materia y gravedad. Igualmente seguimos defendiendo aun en este trabajo, aquel postulado de la relatividad que puso de manifiesto que la masa inercial aparente de los cuerpos, depende del observador, pues esta varia con su densidad y velocidad aparente al igual que el concepto de simultaneidad y por tanto, el espacio que se observa formado por todos los sucesos simultáneos.
Palabras claves: Ecuación del campo de Einstein, Campo Gravitacional, Relatividad General, Relatividad Especial, Campo Gravitatorio, Gravitón, Gravedad Cuántica.
Abstract
Due to the recondite study of the deep secret relation that is between the observed object and the observer in Special relativity, this allows this work that without using tensile terms of matrices nor, also finds how the matter creates gravity, and inversely, how the gravity affects concentrating in a point the matter. Here all this is obtained also starting off indeed of the constant of universal gravitation of Newton, as that force that is determining in the connection between the matter and gravity. Also we continued even defending in this work, that postulate of the relativity that showed that the apparent inertial mass of the bodies, depends on the observer, because this varies with its density and speed pretends like the simultaneidad concept and therefore, the space that is observed formed by all the simultaneous events.
Key Words: of the field of Einstein, Field of gravitation, General Relativity, Special Relativity, Gravitational Field, Graviton, Quantum Gravity.
1. Introducción
Queremos recordar en esta introducción a la ecuación de campo gravitacional y cuántico del gravitón que ya hemos descrito anteriormente. Además vamos a utilizar en el desarrollo de este trabajo también, las dos versiones relativas de la nueva relación de energía-momento con cuadri-Lorentz incluido.
Tomando de la ecuación de campo gravitacional y cuántico del gravitón a la relación general de la constante de gravitación universal de Newton, donde se expresa que por cada kilo de masa única observadora central es decir, donde se expresa de manera universal y genérica el campo gravitacional creado a su alrededor por cada kilogramo de masa central solitaria y observadora de todo lo que sucede a su alrededor ya que de esa manera esta definida la constante Gde gravitación universal:
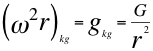 (1)
(1)
Donde ω es una velocidad angular inercial, res la distancia radial que hay desde un punto cualquiera del campo a su alrededor hasta el respectivo centro ocupado por el kilogramo de masa observadora o centro del mismo campo gravitacional, ges la intensidad de gravedad inercial originada por ese kilogramo de masa observadora, Ges la constante de gravitación universal y kges el símbolo de que es una relación expresada por cada kilogramo de masa observadora central y única.
También vamos a recordar a la cantidad de masa involucrada en la constante de Planck o masa de un cuanto:
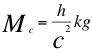 (2)
(2)
Donde Mc es la masa del cuanto, h es la constante de Planck y c la velocidad de la luz en el vacío.
Si tomamos como observador en kilogramos el valor de un cuanto de masa Mccomo observadora y remplazamos el equivalente de Mc especificado en la anterior relación número dos (2), si este lo remplazamos en la también anterior ecuación número uno (1), nos queda la siguiente relación número tres (3) que es para un observador solitario y cuántico:
 (3)
(3)
Donde ω es una velocidad angular inercial, r es la distancia radial que hay desde un punto cualquiera del campo hasta el respectivo cuanto observador o centro del campo gravitacional, gc es la gravedad inercial que origina a su alrededor un cuanto de masa, G es la constante de gravitación universal, hes la constante de Planck y cla velocidad de la luz en vacío.
Pero si a ese único observador descrito en la anterior relación número tres, situado en el centro del campo y observando a todo lo que pasa a su alrededor, precisamente observando a cierta distancia a otro cuanto igual que él y también en reposo inercial u orbital y de masa similar a la propia descrito fielmente por Newton en la siguiente relación número cuatro (4):
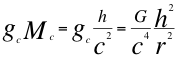 (4)
(4)
Donde gces la gravedad originada por el cuanto central observador, Mc es la masa total del cuanto observado, hes la constante de Planck, cla velocidad de la luz en el vacío, G la constante de gravitación universal y res la distancia que hay entre el relativo cuanto central observador y el cuanto observado.
Ahora vamos a tomar y traer a colación la conclusión de la nueva relación de energía-momento con cuadri-Lorentz incluido, donde se deja identificado y especificado que para una partícula que se aleja del observador, se describe su movimiento con la siguiente ecuación número cinco (5):
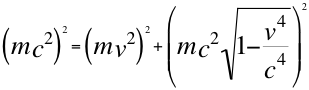 (5)
(5)
Donde m es la masa invariante de la partícula, v es la velocidad resultante de la partícula en dirección contraria al observador y c es la velocidad de la luz.
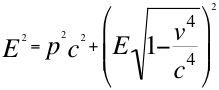 (5)
(5)
Donde E es la energía invariante equivalente a la masa también invariante de la respectiva partícula observada, p es la cantidad de movimiento en dirección contraria al observador, v es la velocidad resultante de la partícula en sentido también contrario al observador y c la velocidad de la luz en vacío.
![]() (6)
(6)
Donde Etes la energía total de todo el movimiento de la partícula que se aleja del observador y que en este caso coincide perfectamente con el valor de la energía invariante equivalente a la concerniente masa también invariante de la respectiva partícula observada, Eces la energía cinética de dicha partícula en dirección contraria al observador y Epes la energía potencial en dirección perpendicular a la recta que une al objeto observado y al observador.
![]() (7)
(7)
![]() (8)
(8)
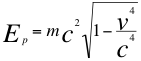 (9)
(9)
También aparece la presentación de la nueva formulación matemática de la cantidad de movimiento para observadores que se alejan del objeto en movimiento:
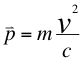 (10)
(10)
Donde p es la Cantidad de movimiento de alejamiento en dirección contraria al observador, m es la masa invariante, v es la velocidad resultante en dirección contraria y de retiro de la partícula y c es la velocidad de la luz.
También dejamos presente en esta introducción que la nueva relación de energía-momento con cuadri-Lorentz incluido, se puede aplicar también al movimiento de una partícula pero en esta ocasión precisamente se acerca al observador, se describe ese movimiento de acercamiento con la siguiente ecuación número once (11):
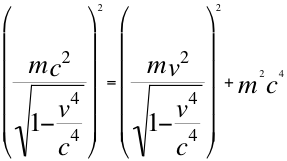 (11)
(11)
Donde m es la respectiva masa invariante de la partícula que se acerca al observador, v es la velocidad resultante de la partícula dirigida hacia el observador y c es la velocidad de la luz.
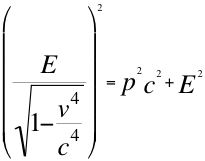 (12)
(12)
Donde E es la energía invariante equivalente a la masa también invariante de la respectiva partícula observada, p la cantidad de movimiento dirigida hacia el observador, v la velocidad resultante de la partícula en dirección hacia el observador y c la velocidad de la luz en el vacío.
![]() (13)
(13)
Donde Etes la energía total de todo el movimiento de la partícula que se acerca al observador y que en este caso no coincide con la energía invariante de la respectiva partícula, Eces la energía cinética de dicha partícula en dirección hacia el observador y Epes la energía potencial de dicha partícula que en este caso es constante y coincide con el valor de la energía invariante de la partícula y equivalente a la respectiva masa invariante de la misma que además sigue siendo perpendicular a la recta que une al observador y el objeto observado.
 (14)
(14)
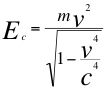 (15)
(15)
![]() (16)
(16)
Donde m es la masa invariante de la partícula observada, v es la velocidad resultante de la partícula en dirección hacia el observador y c es la velocidad de la luz.
Finalmente en esta introducción vamos a recordar a la formulación matemática de p o la cantidad de movimiento para una partícula que se acerca al observador:
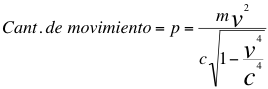 (17)
(17)
Donde p es la cantidad de movimiento dirigida hacia el observador, m es la masa invariante de la partícula observada, v es la velocidad resultante de la partícula dirigida hacia el observador y c es la velocidad de la luz.
2. Desarrollo del Tema.
De la ecuación de campo gravitacional y cuántico del gravitón en la introducción, tomamos la siguiente relación número cuatro (4):
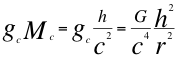 (4)
(4)
Donde gces la gravedad originada por el cuanto observador central, Mc es la masa total del cuanto observado, hes la constante de Planck o energía del cuanto, cla velocidad de la luz en el vacío, Ges la constante de gravitación universal y res la distancia que hay entre el cuanto observador central y el cuanto observado.
En la anterior ecuación número cuatro (4), hes la cantidad de energía que tiene tanto el observador como el objeto observado, por lo tanto la relación de sus energías h/hidentificado como n es igual a uno (1).
Pero resulta que se presentan es valores de energías diferentes en la mayoría de las veces y vamos a identificar entonces a E1 como la energía invariante del objeto observador y a E2 como la energía invariante del objeto observado, y la relación entre E1 y E2 o E1/E2 es igual a n o coeficiente que resulta de la relación de las energías observadoras entre las energías observadas:
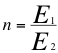 (18)
(18)
![]() (18)
(18)
Remplazando la anterior relación dieciocho (18) en la también anterior relación número cuatro, obtenemos la siguiente relación número diecinueve (19):
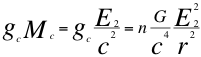 (19)
(19)
Donde gces la gravedad originada por el observador central, Mc es la masa total del objeto observado, E1 es la energía equivalente a la respectiva masa invariante del observador, E2 es la energía equivalente a la respectiva masa invariante del objeto observado, n es el coeficiente relativo de energías, cla velocidad de la luz en el vacío, G la constante de gravitación universal y r es la distancia que hay entre el observador y el objeto observado.
Pero esta anterior relación número diecinueve (19) es una situación en reposo orbital relativo entre el observador y el objeto observado y puede tener dos aplicaciones en cuanto a si el objeto observado se mueve acercándose hacia el observador o, si es lo contrario y efectivamente se encuentra es alejándose del referido observador. Por ejemplo, vamos a ocuparnos primero considerando el caso en que el objeto observado se acerca al observador y en este caso debemos remplazar al E2 de la ecuación diecinueve (19) por la siguiente expresión equivalente pues a E2:
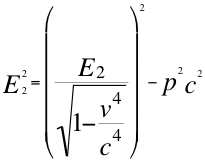 (20)
(20)
Donde E2 es la energía invariante equivalente a la masa también invariante de la respectiva partícula observada, p la cantidad de movimiento del objeto observado dirigida hacia el observador, v la velocidad resultante de la partícula en dirección al observador y c la velocidad de la luz en el vacío.
Entonces remplazando la anterior relación número veinte (20) en la también anterior relación diecinueve (19), nos resulta entonces la siguiente relación número veintiuno (21):
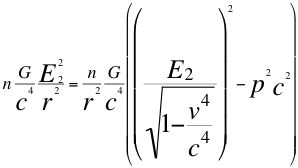 (21)
(21)
Donde n es el coeficiente relativo de energías invariantes entre observador y observado, G la constante de gravitación universal, r es la distancia precisa que hay entre el observador y el objeto observado, E2 es la energía invariante equivalente a la masa también invariante de la respectiva partícula observada, p la cantidad de movimiento resultante del objeto observado en dirección hacia el observador, v la velocidad resultante de la partícula en dirección hacia el observador y c la velocidad de la luz en el vacío.
Pero si el objeto observado se está ahora es precisamente alejando del observador, ya no podemos remplazar la misma relación de acercamiento número veinte (20) en la respectiva ecuación diecinueve (19), pero entonces debemos remplazar es a la siguiente expresión veintidós (22) que describe el movimiento de objetos que se alejan del observador y es precisamente también la misma anterior relación número cinco (5):
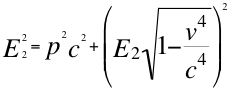 (22)
(22)
Donde E2 es la energía invariante equivalente a la masa también invariante de la respectiva partícula observada, p la cantidad de movimiento resultante del objeto observado en dirección opuesta al observador, v la velocidad resultante de la partícula en dirección opuesta al observador y c la velocidad de la luz en el vacío.
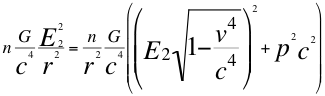 (23)
(23)
Donde n es el coeficiente relativo de energías invariantes, G la constante de gravitación universal, r es la distancia que hay entre el observador y el objeto observado, E2 es la energía invariante equivalente a la masa también invariante de la respectiva partícula observada, p la cantidad de movimiento del objeto observado en dirección opuesta al observador, v la velocidad resultante de la partícula en dirección opuesta al observador y c la velocidad de la luz en el vacío.
Incluso n podría también hasta ser fraccionario en la relación número dieciocho (18) en el caso de que se presente la situación de que el objeto observado, constara de mayor energía invariante que el observador.
3. Conclusiones.
La gran conclusión de este trabajo es la denominada por nosotros “Ecuación General del Campo Gravitatorio” en sus dos grados de libertad de elección en cuanto así el objeto observado se acerque o se aleje del observador:
A)-La ecuación general del campo gravitatorio número veintiuno (21) corresponde a la relación que describe el movimiento de un objeto que se acerca al observador:
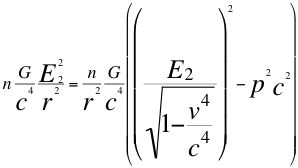 (21)
(21)
Donde n es el coeficiente relativo de energías invariantes entre observador y observado, G la constante de gravitación universal, r es la distancia precisa que hay entre el observador y el objeto observado, E2 es la energía invariante equivalente a la masa también invariante de la respectiva partícula observada, p la cantidad de movimiento resultante del objeto observado en dirección hacia el observador, v la velocidad resultante de la partícula en dirección hacia el observador y c la velocidad de la luz en el vacío.
B)-La ecuación general del campo gravitatorio número veintitrés (23) corresponde a la relación que describe el movimiento de un objeto que se aleja del observador:
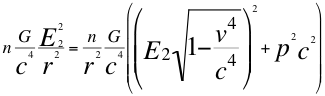 (23)
(23)
Donde n es el coeficiente relativo de energías invariantes, G la constante de gravitación universal, r es la distancia que hay entre el observador y el objeto observado, E2 es la energía invariante equivalente a la masa también invariante de la respectiva partícula observada, p la cantidad de movimiento del objeto observado en dirección opuesta al observador, v la velocidad resultante de la partícula en dirección opuesta al observador y c la velocidad de la luz en el vacío.
C)-Otra gran conclusión de este trabajo es la unificación evidente de la relatividad especial pero modificada, con la relatividad general.
D)-Nos parece apropiado concluir que el espacio cuadrimensional de la relatividad especial también es curvo, igual que el de la relatividad general, aunque sea poco apreciable esa curvatura en el estudio de la radiación electromagnética.
E)-Es imposible dejar de comparar este trabajo con la reconocida ecuación del campo de Einstein y aprovechamos para resaltar coincidencias con unos puntos aclarados por el físico Alemán. Aquí podemos decir que la ecuación general del campo gravitatorio describe con claridad también, como la materia crea gravedad e inversamente, como la gravedad afecta concentrando en un punto a la materia. Este trabajo jamás contradice la curvatura del espacio tiempo y es mas, describe además cómo el espacio se curva también en la relatividad especial. En este trabajo se describe también como la masa de los cuerpos depende del observador y el espacio formado por todos los sucesos simultáneos.
F)-Una gran conclusión es sobre las relaciones número seis (6) y trece (13) de este trabajo, que aunque tienen la misma representación simbólica, constan cada miembros de significados diferentes, ya que una describe es cuando el objeto se aleja del observador y la otra es cuando el objeto se acerca al mismo.
![]() (6)
(6)
![]() (13)
(13)
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
[15] http://www.monografias.com/trabajos-pdf2/matematicas-energia-cinetica-potencial-movimiento/matematicas-energia-cinetica-potencial-movimiento.pdf
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
[44] http://www.monografias.com/usuario/perfiles/pico_jimenez_heber_gabriel
[45] http://www.monografias.com/usuario/perfiles/pico_jimenez_heber_gabriel/monografias
[46] http://www.monografias.com/usuario/perfilprivado/monografias/
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.