Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
Este artículo a través del taquión gravitatorio explica: a la relatividad especial, la relatividad general, el clásico y el inverso experimento de Pound y Rebka, la gravedad cuántica, el colapso de la función de onda en la mecánica cuántica, la misma mecánica cuántica, el efecto Doppler relativista, el corrimiento al rojo, en fin, el taquión podría fácilmente concebirse como una teoría del todo.
Palabras claves: Gravedad Cuántica, Relatividad General, Relatividad Especial, Efecto Doppler Relativista, Corrimiento al Rojo gravitacional.
Abstract
This article through gravitational tachyons explains: to special relativity, general relativity, classic and the inverse experiment of Pound and Rebka, the quantum gravity, the collapse of the function of wave in the quantum mechanics, the same quantum mechanics, the relativist Doppler Effect, the landslide to the red one, in short, the tachyons could easily be conceived like a theory absolutely.
Key Words: Quantum Gravity, General Relativity, Special Relativity, Doppler Effect Relativist, Red landslide to the gravitational one.
1. Introducción
Recordamos en esta introducción a las siguientes relaciones número uno (1) y dos (2), que representa a la misma relación de Newton, fuerza gravitatoria en función de las respectivas masas y energías invariantes:
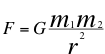 (1)
(1)
 (2)
(2)
Donde G es constante de gravitación universal, m1 y m2 son las masas invariantes de los dos objetos, E1 y E2 son las energías invariantes equivalentes a las respectivas masas invariantes de los objetos a que se refiere Newton, r es la distancia que separa los centros de gravedad de ambos objetos y c es la velocidad de la luz en el vacío.
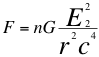 (3) si solo si
(3) si solo si ![]() (4)
(4)
Donde G es constante de gravitación universal, E1 y E2 son las respectivas energías invariantes de los objetos a que se refiere Newton, n es un escalar que define la relación de las respectivas energías invariantes, r es la distancia que separa los centros de gravedad de ambos objetos y c es la velocidad de la luz en el vacío.
También recordamos el principio de conservación de la energía y masa propia manifestado en el concepto de equivalencia entre la masa invariante o en reposo y la energía, que parte del concepto o principio, de suponer a la velocidad de la luz como máxima en la relatividad especial:
![]() (5)
(5)
Donde E es la energía invariante, m es la masa invariante de la partícula y c la velocidad de la luz en el vacío.
También queremos recordar en esta introducción a la geometría de la relatividad especial, donde al clásico espacio euclideo de cuatro dimensiones, se le añade una cuarta dimensión imaginaria icdt, donde i es la unidad imaginaria, ces la velocidad de la luz y dtes la diferencial del tiempo.
![]() (6)
(6)
Donde dses una distancia elemental y dx, dy, dzson la diferenciales del plano cartesiano.
También queremos recordar en esta introducción que en términos actuales de la relatividad especial de Einstein, un taquión sería una partícula hipotética con un cuadrimomento de tipo espacial. Esto implica que si su energía y momento son reales, su masa en reposo convencional aparente sería un número imaginario. Además el tiempo propio que experimenta un taquión es también imaginario. Un curioso efecto es que a diferencia de partículas imaginarias, la velocidad de un taquión crece cuando su energía decrece. La definición formal de la masa de un taquión es sugerida en la siguiente relación:
![]() (7)
(7)
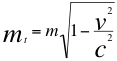 (8)
(8)
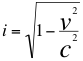 (9)
(9)
Donde mt es la masa imaginaria del taquión, ies la unidad imaginaria y m es la masa invariante de la partícula estudiada.
2. Desarrollo del Tema.
Este trabajo al igual que la relatividad especial de Einstein parte también del principio de que no existe un sistema inercial de referencia privilegiado que se pueda considerar como absoluto. Pero a diferencia de Einstein aquí se propone el postulado de la Invariancia del taquión gravitatorio que sería independiente del movimiento de los cuerpos y la luz. Por otro lado aquí en este artículo se postula una ecuación que representa la equivalencia entre masa y energía E=mT2 donde se indica también que la masa conlleva cierta cantidad de energía aunque se encuentre en reposo.
Este artículo lo iniciamos describiendo también igual que Einstein un espacio de cuatro dimensiones donde añadimos una cuarta dimensión imaginaria iTdt, pero a diferencia de Einstein la cuarta dimensión en nuestro caso, estaría dada por el producto de i como unidad imaginaria, T que es la velocidad finita, constante y superlumínica del taquión gravitatorio y dt la diferencial del tiempo:
![]() (10)
(10)
Donde dses una distancia elemental, dx, dy, dz son la diferenciales del plano cartesiano.
La relación del taquión gravitatorio en un espacio pseudoeclideo, considerando al cuarto vector del tiempo propio imaginario que experimenta el taquión lo tenemos en la siguiente relación:
![]() (11)
(11)
Donde dTes la diferencial de la velocidad del taquión, dx, dyy dzson las diferenciales de las tres coordenadas espaciales, i es la unidad imaginaria, T es la velocidad constante del taquión, dt es la diferencial del tiempo.
![]() (12) y solo si
(12) y solo si 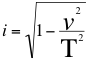 (13)
(13)
Donde T es la velocidad del taquión, vx, vy y vz son las tres velocidades cartesianase ies la unidad imaginaria.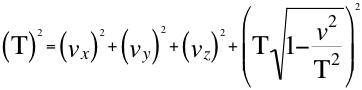 (14)
(14)
Donde T es la velocidad del taquión, vx, vy y vz son las tres velocidades cartesianas, ves la velocidad resultantee ies la unidad imaginaria
Definiendo formalmente la masa en reposo convencional aparente del taquión mt, como una masa imaginaria precisada por el número imaginario i descrito eso si con respecto al mismo taquión en la anterior relación número trece (13), pero expresada ahora en la siguiente relación número quince (15) y dieciséis (16):
![]() (15) Siendo
(15) Siendo ![]() (16)
(16)
Donde mt es la masa imaginaria del taquión, i es la unidad imaginaria, m es la masa de la partícula que se estudia.
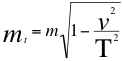 (16a)
(16a)
Remplazando la anterior relación número dieciséis (16) en la también anterior relación número doce (12) nos queda la siguiente relación:
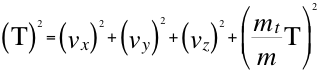 (17)
(17)
![]() (17)
(17)
Donde mt es la masa imaginaria del taquión, mes la masa de la partícula que se estudia, T es la velocidad del taquión, vx, vy y vz son las tres velocidades cartesianas, ves la velocidad resultante de la partícula que se estudia.
Esta anterior relación número diecisiete (17) nos permite encontrar el cuadrivector masa para cualquier partícula con respecto a la masa imaginaria del taquión:
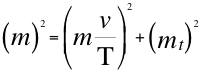 (18)
(18)
Donde mt es la masa imaginaria del taquión, ies la unidad imaginaría, mes la masa de la partícula que se estudia, T es la velocidad del taquión, ves la velocidad resultante de la partícula que se estudia.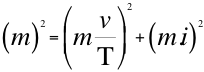 (18)
(18)
En resumen obtenemos las relaciones cuadrivelocidad con respecto a le velocidad del taquión en un espacio de cuatro dimensiones y cuadrimasa con respecto también a la masa imaginaria del taquión que de manera resumida las presentamos en las siguientes relaciones número doce (12) y número dieciocho (18):
![]() (12)
(12)
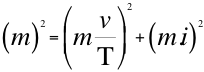 (18)
(18)
Donde mes la masa de la partícula que se estudia, T es la velocidad del taquión, ies la unidad imaginaria, ves la velocidad resultante de la partícula que se estudia.
El cuadrimomento de la partícula m resulta del producto escalar entre su cuadrivelocidad o relación número doce (12) por la cuadrimasa o relación numero dieciocho (18), obteniendo así la siguiente relación número diecinueve (19) y veinte (20) que representa el cuadrimomento y la relación de las energías con respecto a la velocidad del taquión:
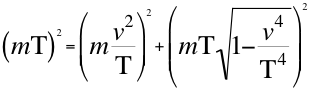 (19)
(19)
Donde mes la masa de la partícula que se estudia, T es la velocidad del taquión, ves la velocidad resultante de la partícula que se estudia.
 (20)
(20)
Donde E=m.T 2 es la energía invariante de la partícula que se estudia, Ec=m.v 2 esla energía cinética de la partícula que se estudia, ves la velocidad resultante de la partícula que se estudia.
Como existiría una velocidad superlumínica, entonces la energía invariante E, equivalente en energía invariante a la respectiva masa invariante mde una partícula, sería igualmente equivalente a E=mT2. Por todo esto creemos que la anterior relación número veinte (20) queda expresada de la siguiente manera:
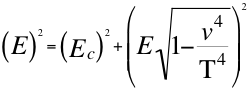 (21)
(21)
Donde Ees la energía invariante de una partícula equivalente a su respectiva masa invariante con respecto al taquión, Ec es la energía cinética de la partícula Ec=m.v 2, ves la velocidad resultante de la partícula que se estudia y T es la velocidad del taquión.
![]() (22)
(22)
Hasta aquí a pesar de que se ha hecho bastante referencia a la energía invariante y energía cinética, no hemos resaltado en la anterior ecuación número veintiuno (21) la presencia de la energía potencial gravitatoria, que es demasiado interesante en la descripción de una relatividad general:
![]() (23) solo si
(23) solo si 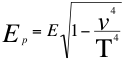 (24)
(24)
Donde Ees la energía invariante de una partícula equivalente a su respectiva masa invariante, Ec es la energía cinética de la partícula Ec=m.v 2, ves la velocidad resultante de la partícula que se estudia, T es la velocidad del taquión y Ep que es la energía potencial gravitatoria de la partícula.
Así de esa manera quedaría expresada una relación que describe el comportamiento de una partícula que se aleja del observador:
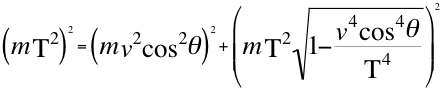
Donde m es la cantidad de masa invariante de la partícula que se observa alejándose, T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, θ es el ángulo descrito entre la trayectoria de la partícula y el observador.
Si ahora detallamos una relación que describa el movimiento de una partícula que se acerca al observador:

Donde m es la cantidad de masa invariante de la partícula que se observa acercándose,T es la velocidad del taquión, v es la velocidad de la partícula en el espacio-tiempo, θ es el ángulo descrito entre la trayectoria de la partícula y el observador.
Estas dos ecuaciones número veinticinco (25) y veintiséis (26) podemos expresarla en función de la energía invariante E, la energía cinética Ec y la energía potencial gravitatoria Ep:
![]() (25)
(25) ![]() (26)
(26)
Donde E es la cantidad de energía invariante de la partícula que se observa alejándose o acercándose al observador, Ec es la energía cinética de la partícula que se aleja o se acerca al observador y Ep que es la energía potencial gravitatoria de la partícula que se aleja o se acerca al observador.
En este momento del artículo vale la pena aclarar que mientras la energía invariante con respecto a la velocidad del taquión E=m.T2 de una partícula es constante, es decir es invariante tanto si la partícula se aleja o se acerca, sin embargo la energía cinética Ec y la Ep potencial gravitatoria se comportan todo lo contrario, ya que varían con respecto a la trayectoria relativa de la partícula referente al observador.
Aplicando la relación original número tres (3) de Newton, pero expresando ahora la energía invariante de los objetos con respecto al taquión y con respecto a la energía invariante de solo uno de los dos objetos a que se refiere el sabio ingles:
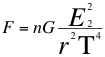 (27)
(27)
Donde F es la fuerza de atracción mutua, n es un escalar que define la relación de las energías invariantes de los objetos, G es la constante de gravitación universal,T es la velocidad del taquión, E2 es la energía invariante del objeto observado, r es la distancia que separa los centros de gravedad de ambos objetos.
Partimos diciendo que esta energía a la que decimos que se refiere Newton en la anterior relación número tres (3), es precisamente la misma energía Ep potencial gravitatoria de las ecuaciones número veinticinco (25) y veintiséis (26), entonces podemos decir lo siguiente:
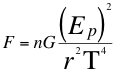 (28)
(28)
Donde F es la fuerza de atracción mutua, n es un escalar que define la relación de las energías invariantes de los objetos, Ep es la energía potencial gravitatoria del objeto observado, G es la constante de gravitación universal, T es la velocidad del taquión, r es la distancia que separa los centros de gravedad de ambos objetos.
Siendo E=m.T2 sabemos que si el cuerpo se aleja del observador la energía Ep potencial gravitatoria equivale a la siguiente relación número veintinueve (29) y si el cuerpo se acerca Ep es equivalente a la siguiente relación número treinta (30):
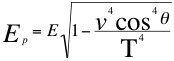 (29)
(29) 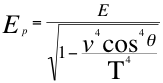 (30)
(30)
Donde E es la cantidad de energía invariante de la partícula que se observa alejándose o acercándose al observador, Ep que es la energía potencial gravitatoria de la partícula que se aleja o se acerca al observador, v que es la velocidad de la partícula en el espacio tiempo, T que es la velocidad del taquión, θ es el ángulo descrito entre la trayectoria de la partícula y el observador.
Remplazando entonces las anteriores relaciones veintinueve (29) y treinta (30) en la anterior relación número veintiocho (28) nos quedan las siguientes relaciones número treintaiuno (31) y treintaidos (32):
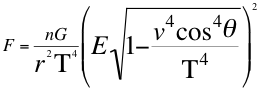 (31)
(31)
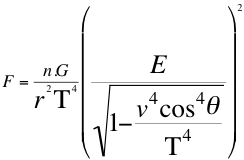 (32)
(32)
Donde F es la fuerza de atracción mutua, n es el escalar que define la relación de las energías invariantes, G es la constante de gravitación universal, E es la energía invariante del objeto observado, r distancia que separa los centros de gravedad, v es la velocidad de la partícula en el espacio tiempo, T que es la velocidad del taquión, θ es el ángulo descrito entre la trayectoria de la partícula y el observador.
Como se puede observar que las anteriores relaciones número treintaiuno (31) y treintaidos (32) son ecuaciones de la relatividad general, ambas relaciones son falseables y de fácil manejo a nivel experimental. Si se ha comprobado la relación de Newton se puede hacer lo mismo con estas relaciones y calcular la velocidad del taquión a partir de ellas.
Gravedad del fotón
Ahora estas relaciones de la relatividad general así descritas respecto al taquión, se les pueden aplicar al fotón, tal como una partícula que se desplaza a la velocidad de la luz de la siguiente forma, es decir para un fotón que se aleja y un fotón que se acerca:
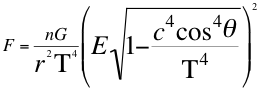 (33)
(33)
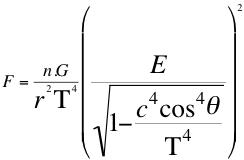 (34)
(34)
Donde F es la fuerza de atracción mutua, n es el escalar que define la relación de las energías invariantes, G es la constante de gravitación universal, E es la energía invariante del fotón observado, r distancia que separa los centros de gravedad, c es la velocidad de la luz con que se aleja o se acerca el fotón, T es la velocidad del taquión, θ es el ángulo descrito entre la trayectoria de la partícula y el observador.
Incluso podemos describir la intensidad de la fuerza de atracción gravitatoria que actúa sobre un fotón que se estrella sobre el astrónomo de Einstein, cuando este encuentra su energía cinética corrida hacia el azul estando aun parado por ejemplo en la superficie de la tierra en la misma trayectoria del fotón:
 (35)
(35)
Donde F es la fuerza de atracción mutua, n es el escalar que define la relación de las energías invariantes, G es la constante de gravitación universal, E es la energía invariante del fotón observado, r distancia que separa los centros de gravedad, c es la velocidad de la luz con que se acerca el fotón, T es la velocidad del taquión.
Aquí en este punto vale la pena resaltar que haciéndole un estimativo al problema del horizonte, donde se observan signos sugestivos de un crecimiento el doble de la real edad del universo, se piensa que el gravitón podía ser el taquión que contara siempre de una velocidad superlumínica desplazándose a través de agujeros negros cuánticos. Sirve más trabajar en las expectativas experimentales con una cifra estimativa de la velocidad del taquión por ejemplo en 1,5C la velocidad de la luz que podía ser incluso hasta mas baja. Si es cierto que es una cifra supuesta y arbitraria, es preciso compararla con la supuesta expansión ultra-rápida que a nadie le consta ni siquiera el por qué ocurrió.
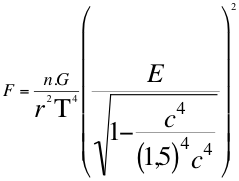 (36)
(36)
Donde F es la fuerza de atracción mutua, n es el escalar que define la relación de las energías invariantes, G es la constante de gravitación universal, E es la energía invariante del fotón observado, r distancia que separa los centros de gravedad, c es la velocidad de la luz con que se acerca el fotón, T es la velocidad del taquión.
La energía cinética de ese fotón que se estrella sobre el astrónomo observador de la superficie de la tierra, va corrida hacia el azul debido a la dilatación por velocidad del tiempo tal como le expresa la siguiente relación:
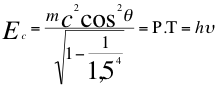 (37)
(37)
Donde Ec es la energía cinética del fotón, m es la masa invariante del fotón, P es una cantidad de movimiento general del fotón, c es la velocidad de la luz en el vacío, h es constante de Planck, υ es la frecuencia del fotón, θ es el ángulo que describe la trayectoria del fotón con el observador, T es la velocidad del taquión.
Este trabajo nos permite unificar a la relación de energía momento, de las llamadas partículas con masa y la relación de energía momento del fotón. Primero describiremos a un fotón que se aleja del observador en la relación número treintaiocho (38), después describiremos a ese mismo fotón con la velocidad estimada del taquión por otro observador a quien se le acerca el fotón, quien lo describe en la relación número treintainueve (39):
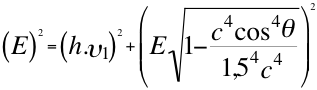 (38)
(38)
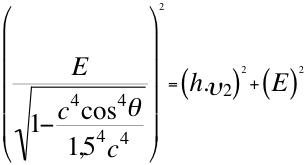 (39)
(39)
![]()
Donde E es la energía invariante del fotón, h es la constante de Planck, υ1 es la frecuencia del fotón alejándose del observador, υ2 es la frecuencia del fotón acercándose al observador, c es la velocidad de la luz en el vacío, θ es el ángulo descrito entre observador y la trayectoria del fotón.
Cantidad de Movimiento “P” del fotón en Relatividad General.
La cantidad de movimiento general P de un fotón que se aleja del observador y también, la cantidad de movimiento general P de ese mismo fotón pero visto ya por otro observador que se acerca respectivamente a él, están expresadas en las siguientes relaciones número cuarenta (40) y cuarentaiuno (41):
![]() (40)
(40)
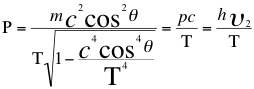 (41)
(41)
Donde P es la cantidad de movimiento general del fotón, m es la masa invariante del fotón, c es la velocidad de la luz en el vacío, h es la constante de Planck, υ es la frecuencia del fotón, p es la cantidad de movimiento especial del fotón, θ es el ángulo descrito entre observador y la trayectoria del fotón, T es la velocidad del taquión.
![]() (41a)
(41a)
Cantidad de Movimiento “p” del fotón en Relatividad Especial.
La relación entre la cantidad de movimiento general P de la relatividad general y la cantidad de movimiento especial p partirán su deducción de acuerdo a la siguiente relación de energía cinética del fotón número cuarenta idos (42):
![]() (42)
(42)
Donde P es la cantidad de movimiento general del fotón, T es la velocidad del taquión, p es la cantidad de movimiento especial reconocido del fotón, c es la velocidad de la luz, h es constante de Planck y λ es la longitud de onda del fotón
Las relaciones entre las respectivas cantidades de movimientos generales y especiales, para un fotón que se aleja la describe la siguiente relación número cuarenta tres (43) y, para un fotón que se acerca la describe la siguiente relación número cuarentaicuatro (44):
![]() (43)
(43)
Donde P es la cantidad de movimiento taquiónico del fotón, p es la cantidad de movimiento lumínico, m es la masa invariante del fotón, h es la constante de Planck, λ1 es la longitud de onda del fotón alejándose del observador, λ2 es la longitud de onda del fotón esta vez acercándose al observador, c es la velocidad de la luz en el vacío, θ es el ángulo descrito entre observador y la trayectoria del fotón, T es la velocidad del taquión.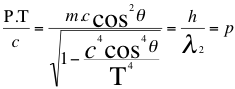 (44)
(44)
![]()
3. Conclusiones.
a)-La gran conclusión de este trabajo es que sin el taquión parece que es totalmente imposible manosear a la gravedad cuántica. Casi todo indica que definitivamente existe una partícula gravitatoria que se desplaza por agujeros negros cuánticos a mayores velocidades que la de la luz y que además de eso, esa partícula se moviliza asimismo a través de esos túneles cuánticos de los que tiene toda la materia incluso el vacío cuántico y que por lo tanto, hace permeable a toda la materia al movimiento oscuro de esas partículas gravitacionales.
Este trabajo permite sostener la descripción también del efecto doppler relativista sobre objetos que se desplazan incluso a la velocidad de la luz.
b)-Si bien es cierto que el espacio y el tiempo no son absolutos en el conjunto del universo ya que este ultimo constituye el cuarto vector del primero, definitivamente este trabajo sostiene que el tiempo iTdt como cuarto vector del espacio, lo define de manera general y para todos los casos precisamente es el taquión y no la velocidad de la luz tal como hasta ahora se ha pensado extender. El tiempo no se detiene para los agujeros negros, para la materia oscura ni la energía oscura. Además este trabajo sostiene que las relaciones de energía momento de la relatividad especial dependen del observador y dejan de ser absolutas.
c)-Determinamos en este trabajo la dilatación gravitacional del tiempo que incrementa la frecuencia de onda, de un fotón que ingresa al campo gravitacional por ejemplo de la tierra y que se dirige hacia el observador de Einstein que está parado en la superficie del planeta. Este mecanismo lo describió el trabajo corrimiento al rojo gravitacional pero de manera inversa y de acuerdo con el experimento de Pound y Rebka cuando el fotón viaja desplazándose hacia el rojo en la altura desde la superficie de la tierra hacia un observador ubicado a cierta altura del planeta. En este trabajo explicaremos ahora con respecto al taquión, es un desplazamiento contrario del fotón, es decir hacia el azul, siendo un fotón que se desplaza hacia abajo desde cierta altura del campo gravitacional directamente hacia la superficie de la tierra.
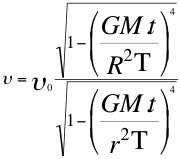 (44) R > r
(44) R > r
Donde υ es la frecuencia tal y como la mediría un observador situado en la superficie del planeta, υo es la frecuencia original emitida por la fuente a cierta altura de la superficie del planeta, M es la masa invariante del planeta, G es la constante de gravitación universal, R es la distancia desde el centro de gravedad del planeta hasta donde está ubicada la fuente que emite el fotón que viaja hacia la superficie de la tierra, r es el radio del planeta, t es el tiempo, T es la velocidad del taquión.
Esta anterior relación número cuarentaicinco (45) coincide con la también anterior relación número treintainueve (39) que recordamos seguidamente y donde, el fotón presenta los efectos de la cantidad de dilatación del tiempo que le corresponde por velocidad, tanto como la cantidad de dilatación del tiempo que le pertenece con el efecto Einstein:
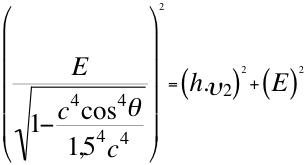 (39)
(39)
Donde E es la energía invariante del fotón, h es la constante de Planck, υ es la frecuencia del fotón acercándose al observador, c es la velocidad de la luz en el vacío, θ es el ángulo descrito entre observador y la trayectoria del fotón, T es la velocidad del taquión.
Insistimos en la aclaración de que la frecuencia υ del fotón en la anterior relación número treintainueve (39), fotón que capta un observador parado en la superficie de la tierra, cuando recibe ese fotón procedente de las alturas, esa frecuencia representa tanto la dilatación del tiempo por velocidad con respecto a la energía invariante del respectivo fotón, como a la cantidad de dilatación gravitacional del tiempo definido por el Pound y Rebka inverso.
d)-El taquión explica el colapso a distancia en el llamado colapso de la función de onda de la mecánica cuántica
e)-Queremos utilizar el inverso del experimento de Pound y Rebka como ejercicio en un Doppler, por esto describimos el efecto Doppler que sufriría un rayo de luz emitido por una fuente que se aleja a un determinado potencial gravitacional y a una velocidad v de la tierra y a R distancia del centro de gravedad expresado en la siguiente relación:

Donde υ es la frecuencia tal y como la mediría un observador situado en la superficie del planeta, υo es la frecuencia original emitida por la fuente que se aleja a cierta altura de la superficie del planeta, v es la velocidad de la fuente que se aleja, θ es el ángulo descrito entre la trayectoria de la fuente y el observador, arf es la aceleración relativa de la fuente con respecto al observador, M es la es la masa invariante del planeta, G es la constante de gravitación universal, R es la distancia desde el centro de gravedad del planeta hasta donde está ubicada la fuente que emite el fotón, r es el radio del planeta, t es el tiempo, T es la velocidad del taquión.
f)-Queremos utilizar también el inverso del experimento de Pound y Rebka como ejercicio en un Doppler, describiendo el efecto Doppler que sufriría un rayo de luz emitido por una fuente que se acerca a un determinado potencial gravitacional y a una velocidad v de la tierra y a R distancia del centro de gravedad:
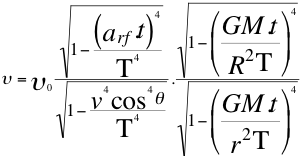
Donde υ es la frecuencia tal y como la mediría un observador situado en la superficie del planeta, υo es la frecuencia original emitida por la fuente que se acerca a cierta altura de la superficie del planeta, v es la velocidad de la fuente que se acerca, θ es el ángulo descrito entre la trayectoria de la fuente y el observador, arf es la aceleración relativa de la fuente con respecto al observador, M es la es la masa invariante del planeta, G es la constante de gravitación universal, R es la distancia desde el centro de gravedad del planeta hasta donde está ubicada la fuente que emite el fotón, r es el radio del planeta, t es el tiempo, T es la velocidad del taquión.
g)-El cuarto vector del tiempo en el espacio es una cantidad de energía invariante imaginaria ya que en el espacio son un total de cuatro vectores, tres de ellos están constituidos por energía cinética y el cuarto por energía invariante imaginaria:
![]()
Donde E es la energía invariante, Ex Ey y Ez son las tres energías cinéticas en el plano cartesiano, i es la unidad imaginaria del tiempo con respecto al taquión.
El tiempo se contrae y se dilata relativamente con respecto al observador, la gravedad trabaja precisamente es con el tiempo, ya sea en contracción o dilatación y vale decir, la masa de los cuerpos depende del observador.
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[01] Relatividad General
[02] Relatividad General
[03] corrimiento al rojo gravitacional
[04] efecto doppler relativista
[05] corrimiento al rojo
[06] corrimiento al rojo gravitacional
[07] efecto doppler relativista
[08] efecto doppler relativista
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
[15] http://www.monografias.com/trabajos-pdf2/matematicas-energia-cinetica-potencial-movimiento/matematicas-energia-cinetica-potencial-movimiento.pdf
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.