Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
En este trabajo la “ley universal de efecto Doppler” se aplica también a las ondas gravitacionales describiendo a la gravedad como un Doppler gravitacional, además se demuestra aquí también la consistente relatividad que hay en la ocurrencia y geometría relativa de los agujeros negros. Es decir, para nosotros en el sistema solar utilizando la constante gravitacional de Newton en la métrica de Schwarzschild, se pueden obtener singularidades matemáticas en otros sistemas diferentes al sistema solar, se encuentra así un agujero negro que no emitiría ondas gravitacionales para nosotros porque no contamos con su correspondiente aceleración, aunque en realidad para un observador ubicado en ese mismo sistema que lo alberga y contiene con igual aceleración no le resulte tal agujero negro. Observemos que nosotros en sí aquí en el sistema solar a través de la nata métrica de Schwarzschild; no obtenemos matemáticamente agujeros negros nativos.
Palabras claves: Agujeros negros, Ondas Gravitacionales, Gravedad, Doppler Relativista, Dilatación gravitacional del Tiempo, Corrimiento al Rojo gravitacional.
Abstract
In this work the "universal law of Doppler" also applies to gravitational gravity to portray as a gravitational Doppler also demonstrated here also consistent relativity on the occurrence and on geometry of black holes waves. I.e. for us solar using Newton's gravitational constant in the Schwarzschild metric system, get math singularities on other systems than the solar system, a black hole that would not issue for us gravitational waves because we do not have their corresponding acceleration, although not actually located in the same system that hosts it and contains with equal ease Observer makes such black hole is thus. Let's look at us itself here in the solar system through the cream; Schwarzschild metric we do not mathematically get native black holes.
Key Words: Black holes, waves Gravitacionales, gravity, relativistic Doppler, gravitational dilatation of time, landslide the gravitational red.
1. INTRODUCCIÓN
Como introducción de este artículo queremos recordar las conclusiones del anterior trabajo de la dilatación gravitacional del tiempo en la ley universal del efecto Doppler.
La descripción y el desarrollo de artículo tienen como principio de que si se hace el estudio completo del Doppler, es necesario incluir a la velocidad y trayectoria tanto de la fuente como del observador, que serán descompuestas cada una en dos componentes con respecto al ángulo que describen las trayectorias de cada uno en relación a la recta de vista que los une. Habrán dos vectores que comparten la misma recta de acción y aplicados fijamente en los extremo de dicha recta de visión, estarán situados allí los cosenos de los respectivos ángulos que describen la trayectoria de la fuente y observador vfcosθf y vocosθo con la línea de vista. Vectores que tendrían la misma dirección que podía ser en el mismo sentido o sentido contrario. Por el otro lado estaría el seno del ángulo descrito entre la trayectoria de la fuente y observador vfsenθf y vosenθo que serían siempre paralelas en uno u otro sentido en el mismo plano.
![]() (1)
(1)
![]() (2)
(2)
Donde vf es la velocidad de la fuente, θf es el ángulo descrito entre la línea de visión del observador y la trayectoria de la fuente, vo es la velocidad del observador, θo es el ángulo descrito entre la línea de visión y la trayectoria del observador.
Ahora aplicamos la “Ley universal del efecto Doppler” donde quedan implícitas las velocidades y trayectorias de la fuente y observador: “El cuadrado de la relación entre las frecuencias emitida y observadas más, el cuadrado de la relación entre la velocidad de la fuente y la onda más, el cuadrado de la relación de la velocidad del observador y la onda es igual a la unidad”.
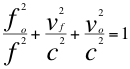 (3)
(3)
Donde fo es la frecuencia emitida por la fuente, f es la frecuencia medida por el observador, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació.
Vamos a aplicar la ley universal del efecto Doppler a los cosenos de los respectivos ángulos fuente y observador para encontrar o identificar a fz que es la frecuencia emitida de la fuente corrida hacia el azul:
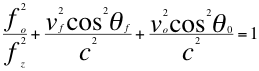 (4)
(4)
Donde fo es la frecuencia emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la línea de visión.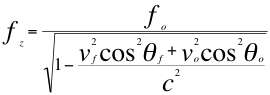 (5)
(5)
Ahora vamos a aplicar la ley universal del efecto Doppler a los senos de los respectivos ángulos y a calcular a la frecuencia final definitiva que seguramente tendría corrimiento hacia el rojo:
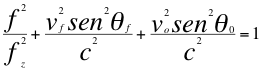 (6)
(6)
Donde f es la frecuencia observada, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
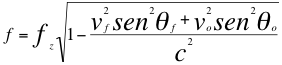 (7)
(7)
Reemplazando a fz de la anterior relación número cinco (5) en la también anterior relación número siete (7) nos queda la siguiente ecuación número ocho (8):
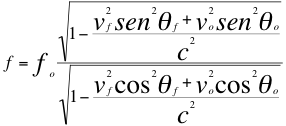 (8)
(8)
![]()
Donde f es la frecuencia observada, fo es la frecuencia emitida por la fuente, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
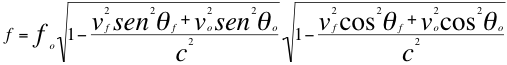 (9)
(9)
![]()
Las anteriores relaciones número ocho (8) y nueve (9) son las ecuaciones que describen el Doppler relativista cuando la fuente y observador se acercan o se alejan incluso con desiguales velocidades angulares.
Para el Doppler relativista en las ondas electromagnéticas es descrita por las anteriores relaciones pero, para el Doppler sonoro quedaría de la siguiente manera:
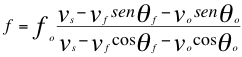 (10)
(10)
Donde f es la frecuencia observada, fo es la frecuencia emitida por la fuente, vs es la velocidad del sonido, vf es la velocidad de la fuente, vo es la velocidad del observador, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
EXPERIMENTO DE POUND Y REBKA
Si un observador a cierta altura de la superficie de la tierra y con cierta velocidad angular ocasionada por la carga rotatoria en reposo, mira una fuente también en reposo con carga rotatoria simétricamente esférica también ubicada en la superficie del planeta. Fuente y observador presentan similares velocidades angulares porque soportan la misma carga rotatoria pero describen diferentes velocidades lineales, velocidades que si la dividimos en sus dos componentes ortogonales con respecto a sus respectivos ángulos descritos en su trayectoria son, la componente vfcosθf para la fuente y vocosθo para el observador, incluso que son nulas porque ellos ni se acercan ni se alejan relativamente entre sí. El Doppler que se describe entonces entre ellos es un Doppler transversal porque el ángulo θf y θo descritos son ambos de 90 grados. Tal como lo plantea el experimento de Pound y Rebka. Entonces la velocidad que llevan la fuente y el observador respectivamente es totalmente la velocidad tangencial originada por la carga rotatoria de cada uno o sea vfsenθf y vosenθo de la siguiente manera a sabiendas de que senθf =1=senθo:
![]() (11)
(11)
Donde vf es la velocidad de la fuente, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión con el observador, r es el radio del planeta, T es el periodo y ω es la velocidad angular de la fuente.
![]() (12)
(12)
Un observador que está hipotéticamente ubicado en reposo a cierta altura h del planeta con igual velocidad angular que la fuente de la superficie, por la carga rotatoria describe también una componente tangencial de la velocidad en el mismo sentido y dirección, entonces se incluye también en la ley universal del efecto Doppler a la velocidad tangencial del observador de la siguiente manera:
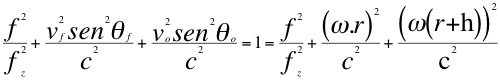 (13)
(13)
Donde fz =fo es la frecuencia emitida por la fuente, f es la frecuencia tal como la mediría un observador situado en reposo a mayor altura, r es el radio del planeta, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión con observador, ω es la velocidad angular de la fuente y observador,hes a la altura sobre la superficie del planeta donde se encuentra el observador, c es la velocidad de la luz.
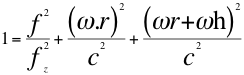 (14)
(14)
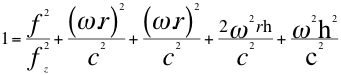 (15)
(15)
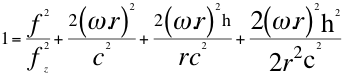 (16)
(16)
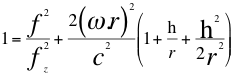 (17)
(17)
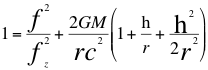 (18)
(18)
Donde fz=fo es la frecuencia emitida por la fuente, f es la frecuencia tal como la mediría un observador a mayor altura, r es el radio del planeta, G es la contante de gravitación universal, M es la masa del planeta, c es la velocidad de la luz,hes a la altura sobre la superficie del planeta donde se encuentra el observador.
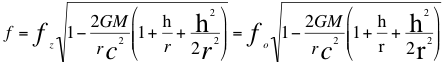 (19)
(19)
Donde fz=fo es la frecuencia emitida por la fuente, f es la frecuencia tal como la mediría un observador a mayor altura, r es el radio del planeta, G es la contante de gravitación universal, M es la masa del planeta, c es la velocidad de la luz,hes a la altura sobre la superficie del planeta donde se encuentra el observador.
2. DESARROLLO DEL TEMA.
Partiendo de que la perspectiva de un observador estacionario corresponde al tiempo propio local en cada región del espacio tiempo, dependiendo de una diferencia en el paso del tiempo propio en diferentes posiciones definidas por un tensor métrico del espacio tiempo. Cada región infinitesimal de espacio tiempo puede tener su propio tiempo propio, que corresponde a la dilatación temporal gravitatoria en dicho punto, sitio donde la radiación electromagnética y la materia son afectadas por igual, puesto que están compuestas de la misma esencia. Tales regiones son significativas, sin importar si están o no ocupadas por algún observador.
Partimos el desarrollo de este trabajo desde las anteriores relaciones número ocho (8) y nueve (9) de la introducción, relaciones que resultan idóneas de aplicación original para el estudio del Doppler inercial de las ondas electromagnéticas como quedó demostrado en el experimento de Pound Rebka pero y si las ondas gravitacionales se transmiten en realidad a la misma velocidad de la luz, entonces también se pueden aplicar a un marco de referencia acelerado que de origen a las ondas gravitatorias, aunque no arrojen resultados recíprocos como en la luz porque en realidad las gravitacionales son ondulaciones del espacio-tiempo unidireccionales, producidas por una densidad de masa aparente acelerada, cuestión que hace que el tiempo sea un tiempo propio para cada región gravitacional, entonces la fuente o partícula observada como fuente acelerada tiene también una densidad de masa M aparente acelerada y tiempo propio que le permite emitir determinada cantidad de onda gravitatoria a cierta frecuencia gravitatoria fo original no reciproca, pues f es entonces la frecuencia gravitatoria medida por un observador estacionario igualmente acelerado y ubicado a cierta distancia de la respectiva fuente M. Las siguientes relaciones número veinte (20) y veinte y uno (21) son las relaciones de fuente y observador cuando se acercan o se alejan respectivamente:
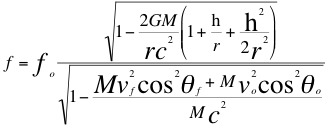 (20)
(20)
![]()
Donde f es la frecuencia gravitatoria observada a cierta altura por un observador estacionario, fo es la frecuencia gravitatoria emitida por la fuente, M es la masa de la fuente gravitatoria, G es la constante de gravitación universal,h es la altura medida desde la superficie de la masa de la fuente hasta donde se encuentra ubicado el observador estacionario, r es el radio de la masa de la fuente, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
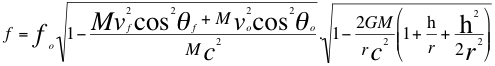 (21)
(21)
![]()
Donde f es la frecuencia gravitatoria observada, fo es la frecuencia gravitatoria emitida por la fuente, M es la masa de la fuente gravitatoria, G es la constante de gravitación universal,h es la altura medida desde la superficie de la masa de la fuente hasta donde se encuentra ubicado el observador, r es el radio de la masa de la fuente, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
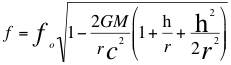 (21)
(21)
En estas relaciones como el tiempo es un tiempo propio no reciproco de cada región gravitacional entonces la frecuencia gravitatoria f recibida por el observador estacionario se corresponde con el tiempo de la frecuencia fo que es la frecuencia gravitatoria emitida por la fuente con masa M. El inverso de las anteriores relaciones número veinte (20) y veinte y uno (21) invertidas, se traducen en las siguientes relaciones número veinte y dos (22) y veinte y tres (23):
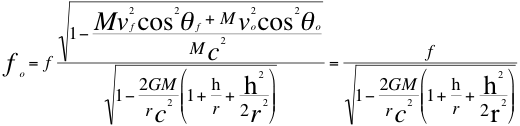 (22)
(22)
![]()
Donde fo es la frecuencia gravitatoria observada en la fuente, f es la frecuencia gravitatoria recibida por el observador, G es la constante de gravitación universal, M es la masa de la fuente gravitatoria, h es la altura medida desde la superficie de la masa de la fuente gravitatoria hasta donde se encuentra ubicado el observador, r es el radio de la masa de la fuente gravitatoria, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
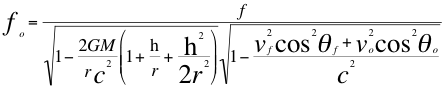 (23)
(23)
![]()
Aquí en este momento es cuando aparece la posibilidad matemática de que de pronto se forme una región específica y finita del espacio-tiempo con gran concentración de masa que sobrepase a los límites impuestos por la constante de gravitación universal de Newton en el sistema solar.
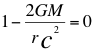 (24)
(24)
Donde G es constante de gravitación universal, M es la masa del astro o planeta del sistema solar, r es el radio del planeta y c la velocidad de la luz.
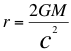 (25)
(25)
Radio de Schwarzschild en el sistema solar.
Lo difícil de esa posibilidad según este trabajo es que al parecer, la gravedad se postula como un Doppler transversal gravitacional descrito por la onda gravitatoria emitida por una masa acelerada y entonces una masa como la de un agujero negro, no puede quedar sin pelo y sin emitir ondas gravitacionales, mucho menos si tiene tan concentrada masa como se pretende la constitución de tal singularidad.
Entonces quedan dos posibilidades, una primera sería muy poco probable que la onda gravitacional se transmita en realidad a mayor velocidad que la luz o, la segunda más factible es que la constante de gravitación universal sea diferente para cada momento angular de cada sistema gravitatorio formado alrededor de una determinada masa central.
Vale la pena recordar en estos momentos que la constante G de gravitación universal de Newton en el sistema solar, fue calculada como aquella densidad o cantidad de constante de Kepler del sistema solar, por cada kg de masa central solar.
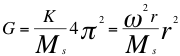 (26)
(26)
Donde G es la constante de gravitación universal de Newton en el sistema solar, K es la constante de Kepler para el sistema solar, Ms es la masa del sol, ω es la velocidad angular, π es una constante elemental y r es el radio de los planetas alrededor del sol.
Es probable que esta misma relación de Kepler por kg K/MS de masa central en el sistema solar, no sea exactamente igual en los demás sistemas gravitatorios del universo diferente al sistema solar, sobretodo en masas centrales con elevado índice de momento angular.
Esta última factibilidad si ocurre altera inmediatamente a la velocidad de escape y al radio de Schwarzschild para ese planeta de masa semejante a la masa por ejemplo de la tierra, que si girara hipotéticamente en otro sistema alrededor de otra masa central por ejemplo masa central que fuera equivalente a varias masas solares.
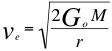 (27)
(27)
Donde ve es la velocidad de escape de la masa de la tierra en un sistema distinto al solar, Go es la constante de gravitación universal para ese otro sistema, M es la masa de la tierra acá y en ese otro hipotético sistema y r es el radio de la tierra acá y en ese hipotético sistema gravitacional.
 (28)
(28)
Radio de Schwarzschild de la masa de la tierra en ese otro sistema gravitatorio hipotético.
Por esto se puede decir con seguridad que en un campo gravitatorio similar al sistema solar, puede usarse aproximadamente la métrica de Schwarzschild para describir localmente la geometría del espacio-tiempo dentro del sistema solar, que aproximadamente tiene simetría esférica, dado que el sol tiene un momento angular pequeño. Pero estudiar a otro sistema con esta métrica estaríamos describiendo matemáticamente la ocurrencia de falsos agujeros negros.
3. CONCLUSIONES.
a)-la ley universal del efecto Doppler para las ondas gravitacionales queda de la siguiente manera: La relación entre el cuadrado de la frecuencia emitida y observada más, la relación entre el cuadrado de la velocidad angular de la fuente y la velocidad de la onda mas, la relación entre el cuadrado de la velocidad angular del observador y la velocidad de la onda, es igual a la unidad:
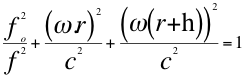 (29)
(29)
Donde fo es la frecuencia gravitacional emitida por la fuente, f es frecuencia gravitacional observada, ω es la velocidad angular de la fuente y el observador, r es el radio de la masa de la fuente y h es la altura del observador.
El principio de equivalencia implica que un observador para poder sentir el Doppler de las ondas gravitatorias procedentes de una fuente gravitacional, irremediablemente necesita hallarse también correctamente acelerado conservando el reposo necesario en un punto cualquiera de la geometría local del espacio-tiempo de un campo gravitatorio.
b)-Como primera conclusión un observador a la altura h, como cosθf=0 y cosθo=0 entonces siente un Doppler transversal gravitatorio de una onda precisamente gravitatoria procedente de la fuente acelerada M, de acuerdo a la siguiente relación:
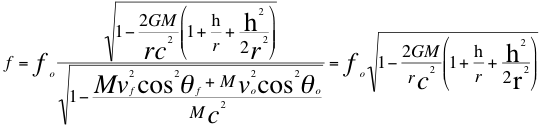
![]()
Donde fo es la frecuencia gravitatoria observada en la fuente, f es la frecuencia gravitatoria recibida por el observador, G es la constante de gravitación universal, M es la masa de la fuente gravitatoria, h es la altura medida desde la superficie de la masa de la fuente gravitatoria hasta donde se encuentra ubicado el observador, r es el radio de la masa de la fuente gravitatoria, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
c)-Como segunda conclusión presentamos la siguiente relación:
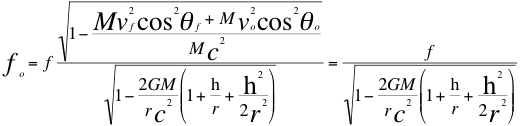
![]()
Donde fo es la frecuencia gravitatoria observada en la fuente, f es la frecuencia gravitatoria recibida por el observador, G es la constante de gravitación universal, M es la masa de la fuente gravitatoria, h es la altura medida desde la superficie de la masa de la fuente gravitatoria hasta donde se encuentra ubicado el observador, r es el radio de la masa de la fuente gravitatoria, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[01] Relatividad General
[02] Relatividad General
[03] corrimiento al rojo gravitacional
[04] efecto Doppler relativista
[05] corrimiento al rojo
[06] corrimiento al rojo gravitacional
[07] efecto doppler relativista
[08] efecto doppler relativista
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
[15] http://www.monografias.com/trabajos-pdf2/matematicas-energia-cinetica-potencial-movimiento/matematicas-energia-cinetica-potencial-movimiento.pdf
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.