Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
En este trabajo se identifica la naturaleza física de los agujeros negros a través de la “LUED”. Se encuentra que en la relatividad especial el cuadrado de la velocidad de escape, es igual a la suma del cuadrado de la velocidad de la fuente de ondas electromagnéticas en el Doppler transversal relativista, más el cuadrado de la velocidad del observador. También se puede decir según este artículo que el cuadrado de la velocidad de escape en la relatividad general, es igual a la suma del equivalente del cuadrado de la velocidad de la fuente de ondas gravitatorias que es precisamente igual a la aceleración gravitacional de la fuente masiva por el radio de la misma, más el producto de la respectiva aceleración gravitacional del observador con respecto a la fuente de ondas por su radio propio. Es decir, este trabajo encuentra a través de la “LUED” que la velocidad de escape y los agujeros negros son reales conceptos gravitacionales, que le pertenecen enteramente al estudio del Doppler transversal relativista de ondas gravitatorias y por esto, es que la velocidad de escape de un observador es independiente de la masa que pueda tener dicho observador como proyectil.
Palabras claves: Horizonte de Sucesos, Agujeros Negros, Masa Imaginaria, Doppler Transversal, Tiempo Propio, Masa Aparente, Gravedad Cuántica, Doppler Relativista, Dilatación gravitacional del Tiempo.
Abstract
This paper identifies the physical nature of black holes of the "LUED". It is that in special relativity exhaust velocity squared is equal to the sum of the square of the speed of the source of electromagnetic waves in the transversal relativistic Doppler over the square of the speed of the observer. According to this article that the square of general relativity, escape velocity is equal to the sum of the equivalent of the square of the speed of the source of gravitational waves that equals precisely gravitational acceleration massive supply radio, plus product of respective gravitational acceleration of the observer with the source of waves by his own radio can also be said. I.e., this work is through the "LUED" escape velocity, and black holes are real gravitational concepts belonging entirely to the study of the transversal relativistic Doppler gravity wave and why, is an observer escape velocity is independent of the mass that could have the observer as a projectile.
Key Words: Horizon of events, black holes, mass imaginary, Transversal Doppler, own time, apparent mass, quantum gravity, relativistic Doppler, gravitational time dilation.
1. INTRODUCCIÓN
Queremos iniciar esta introducción definiendo que L.U.E.D. son las iniciales de la “Ley Universal del Efecto Doppler”.
En esta corta introducción vamos a hacer una referencia rápida de lo que actualmente está aceptado en la comunidad científica, para calcular la velocidad de escape en los cuerpos masivos.
La velocidad de escape es la velocidad mínima con la que debe lanzarse el cuerpo para que escape de la atracción gravitatoria de la Tierra o de cualquier otro astro. Esto significa que el cuerpo o proyectil no volverá a caer sobre la Tierra o astro de partida, quedando en reposo a una distancia suficientemente grande (en principio, infinita) de la Tierra o del astro.
A velocidades inferiores a la de escape, el proyectil se convertiría en un satélite artificial en órbita elíptica alrededor del astro que lo atraiga. Según las dimensiones del astro y la velocidad inicial del proyectil, puede ocurrir que esa trayectoria elíptica se complete o que termine en colisión con el astro que atrae al proyectil. En este segundo caso, suele aproximarse la trayectoria elíptica por una parábola (Tiro parabólico).
Para calcular la velocidad de escape, se usan las siguientes formulas relacionadas con la energía cinética y potencial:
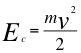 (1)
(1) ![]() (2)
(2)
Donde Ec es la energía cinética, m es la masa del proyectil, v es la velocidad de escape, Ep es la energía potencial, G es la constante de gravitación universal, M es la masa cuerpo másico y r es el radio del cuerpo masivo.
El principio de conservación de la energía, al que imponemos la condición de que el objeto se aleje hasta una distancia infinita y quede en reposo:
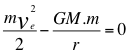 (3)
(3) 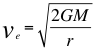 (4)
(4)
Donde ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa del astro, m es la masa del proyectil y r es radio del astro
2. DESARROLLO DEL TEMA.
La “Ley universal del efecto Doppler” (LUED) dice “La relación entre el cuadrado de la frecuencia emitida y percibida, más la relación entre el cuadrado de la velocidad de la fuente y la velocidad de la onda, más la relación entre el cuadrado de la velocidad del observador y la velocidad de la onda, es igual a la unidad.
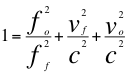 (5)
(5)
Donde fo es la frecuencia percibida por el observador, ff es la frecuencia emitida por la fuente de ondas electromagnéticas, vf es la velocidad de la fuente, vo es la velocidad del observador y c es la velocidad de la luz.
La “Ley universal del efecto Doppler” (LUED) se le puede aplicar tanto a la dilatación por velocidad del tiempo en la relatividad especial como a la dilatación gravitacional del tiempo en la relatividad general.
DILATACIÓN POR VELOCIDAD DEL TIEMPO A TRAVES DE LA “LUED”
Aplicando pues esta ley universal del efecto Doppler “LUED” en la dilatación por velocidad del tiempo, tal como si no existiera en la naturaleza la dilatación gravitacional del tiempo, aplicándosela a una fuente de ondas electromagnéticas situada en la superficie de un cuerpo masivo como la tierra y observada a cierta altura tal como se hizo con el experimento de Pound Rebka, descrito de la siguiente manera con la relación inicial con respecto al seno del ángulo de la velocidad de la fuente y del observador:
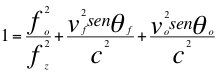 (6)
(6)
Donde fo es la frecuencia de ondas electromagnéticas tal y como le percibe un observador a cierta altura de un cuerpo másico, fz es la frecuencia emitida por la fuente de ondas electromagnéticas pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, θf es el ángulo de la fuente con respecto al observador, θo es el ángulo del observador con respecto a la fuente y c la velocidad de la luz.
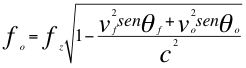 (7)
(7)
La siguiente es la misma relación anterior pero expresada en función del coseno del ángulo de la velocidad de la fuente de ondas electromagnéticas y del observador:
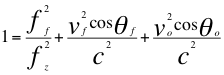 (8)
(8)
Donde ff es la frecuencia emitida por una fuente de ondas electromagnéticas en la superficie de un cuerpo másico, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente en la superficie del cuerpo masivo, vo es la velocidad del observador a cierta altura del objeto masivo, θf es el ángulo de la fuente con respecto al observador, θo es el ángulo del observador con respecto a la fuente y c la velocidad de la luz.
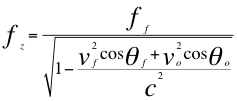 (9)
(9)
Remplazando a la relación número nueve (9) en la anterior relación número siete (7) nos resulta la siguiente relación:
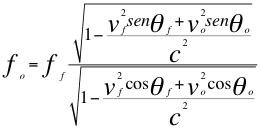 (10)
(10)
Donde ff es la frecuencia emitida por una fuente de ondas electromagnéticas ubicada en la superficie de un cuerpo másico, fo es la frecuencia tal y como la percibe un observador a cierta altura, vf es la velocidad de la fuente en la superficie del cuerpo masivo, vo es la velocidad del observador a cierta altura del objeto masivo, θf es el ángulo de la fuente con respecto al observador, θo es el ángulo del observador con respecto a la fuente y c la velocidad de la luz.
Cuando un observador en reposo percibe o mide una frecuencia procedente de la superficie de un cuerpo másico como en el experimento de Pound Rebka, se configura es un Doppler transversal por que los ángulos θf y θo quedan de un valor de 90 grados y la relación subsiste de la siguiente manera:
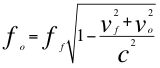 (11)
(11)
Donde ff es la frecuencia emitida por una fuente de ondas electromagnéticas ubicada en la superficie de un cuerpo másico, fo es la frecuencia tal y como la percibe un observador a cierta altura, vf es la velocidad de la fuente en la superficie del cuerpo masivo, vo es la velocidad del observador a cierta altura del objeto masivoy c la velocidad de la luz.
Aquí es donde se encuentra la columna vertebral de este artículo por que el cuadrado de la velocidad de la fuente de ondas electromagnéticas más el cuadrado de la velocidad del observador es igual al cuadrado de la velocidad de escape que en la dilatación del tiempo por velocidad no significa nada, pero en la dilatación gravitacional del tiempo en ondas gravitacionales es de mucho interés:
![]() (12)
(12)
Donde ve es la velocidad de escape, vf es la velocidad de la fuente y vo es la velocidad del observador.
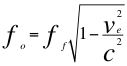 (13)
(13)
Donde ff es la frecuencia emitida por una fuente de ondas electromagnéticas ubicada en la superficie de un cuerpo másico, fo es la frecuencia tal y como la percibe un observador a cierta altura, ve es la velocidad de escape y c la velocidad de la luz.
DILATACIÓN GRAVITACIONAL DEL TIEMPO A TRAVES DE LA “LUED”
Pero resulta que la “La ley universal del efecto Doppler” (LUED) también se le puede aplicar a la dilatación gravitacional del tiempo de la siguiente manera:
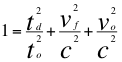 (14)
(14)
Donde to es el tiempo propio para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, td es el tiempo propio para un observador lento que está ubicado dentro de un campo gravitacional, vf es la velocidad de de la fuente de ondas gravitacionales, vo es la velocidad del observador lento que está dentro del campo gravitacional y c la velocidad de la luz.
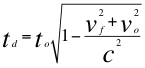 (15)
(15)
Donde to es el tiempo propio para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, td es el tiempo propio para un observador lento dentro del campo gravitacional, vf es la velocidad de la fuente de ondas gravitacionales, vo es la velocidad del observador lento que está dentro del campo gravitacional, ve es la velocidad de escape y c la velocidad de la luz.
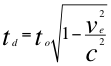 (16)
(16) ![]() (12)
(12)
Donde to es el tiempo propio para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, td es el tiempo propio para un observador lento dentro del campo gravitacional, vf es la velocidad de la fuente de ondas gravitatorias, vo es la velocidad del observador lento de ondas electromagnéticas y que está dentro del campo gravitacional, ve es la velocidad de escape y c la velocidad de la luz.
Podemos ver que la velocidad de escape en la dilatación por velocidad del tiempo donde se estudian es ondas electromagnéticas, es diferente a la velocidad de escape calculada en la dilatación gravitacional del tiempo donde se estudian son ondas gravitacionales, que aunque tienen la misma velocidad que las ondas electromagnéticas, se utilizan son los equivalentes en unidades a los cuadrados de las velocidades de la fuente y del observador como son el producto de las aceleraciones gravitacionales de la fuente masiva de ondas gravitacionales por el propio radio, tanto de la fuente másica como del observador, por lo tanto en este cálculo gravitacional que es el que nos sirve en la siguiente descripción de la velocidad de escape:
Entonces remplazando en la anterior relación número doce (12) al producto de las aceleraciones gravitacionales por el radio de la fuente de ondas gravitacionales o cuerpo masivo y la aceleración gravitacional del observador por el radio del observador lento que está ubicado dentro del campo gravitatorio, produce una relación descrita de la siguiente manera:
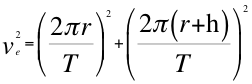 (17)
(17)
Donde ve es la velocidad de escape, π es una constante geométrica, Tes el período, r es el radio del objeto masivo y h la altura del observador lento dentro del campo gravitacional.
![]() (18)
(18)
Donde ve es la velocidad de escape, ω es la velocidad angular de la fuente de ondas gravitatorias y el observador lento dentro del campo gravitacional, r es el radio del cuerpo másico y h es la altura donde ubicado el observador lento dentro del campo gravitacional.
![]() (19)
(19)
Donde ve es la velocidad de escape, ω es la velocidad angular de la fuente de ondas gravitatorias y el observador lento que está dentro del campo gravitacional, r es el radio del cuerpo másico y h es la altura donde ubicado el observador lento que está dentro del campo gravitacional.
En esta anterior relación número diez y nueve (19) reemplazamos a los respectivos productos de las aceleraciones gravitacionales por su radio y entonces queda descrita la relación de la velocidad de escape de una fuente de ondas gravitatorias de la siguiente manera:
![]() (20)
(20) ![]() (12)
(12)
Donde ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o del cuerpo másico, r es el radio del objeto masivo, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional, vf es la velocidad de la fuente de ondas electromagnéticas y vo es la velocidad del observador de ondas electromagnéticas.
![]() (20a)
(20a) ![]() (20b)
(20b)
Donde vf es el equivalente en unidades a la velocidad de la fuente pero en ondas gravitacionales, vo es el equivalente a la velocidad del observador pero en ondas gravitacionales, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o del cuerpo másico, r es el radio del objeto masivo, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional.
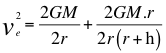 (21)
(21)
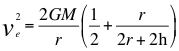 (22)
(22)
Donde ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o del cuerpo másico, r es el radio del objeto masivo, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional.
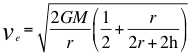 (23)
(23)
Donde ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo másico, r es el radio del objeto masivo, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional.
Esta relación anterior se describe el valor de la velocidad de escape para ese observador lento que está dentro del campo gravitacional a esa altura. Pero resulta que si el observador está ubicado en la superficie de la fuente o cuerpo masivo la velocidad de escape es la siguiente.
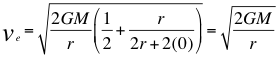 (24)
(24)
Donde ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo másico, r es el radio del objeto masivo, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional.
Volvamos nuevamente a la anterior ecuación número diez y seis (16) que describe el tiempo propio del observador lento y remplazamos en ella a la velocidad de escape descrita en la también anterior relación número veinte y dos (22):
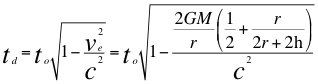 (25)
(25)
Donde to es el tiempo propio para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, td es el tiempo propio para un observador lento dentro del campo gravitacional, ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo masivo, r es el radio del cuerpo másico, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional y c la velocidad de la luz.
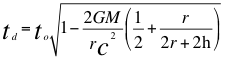 (26)
(26)
Donde to es el tiempo propio para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, td es el tiempo propio para un observador lento dentro del campo gravitacional, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo masivo, r es el radio del cuerpo másico, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional y c la velocidad de la luz.
El tiempo propio para un observador lento ubicado en la superficie de un cuerpo másico es el siguiente:
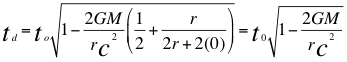 (27)
(27)
Donde to es el tiempo propio para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, td es el tiempo propio para un observador lento dentro del campo gravitacional, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo masivo, r es el radio del cuerpo másico, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional y c la velocidad de la luz.
DILATACIÓN GRAVITACIONAL DE LA MASA A TRAVES DE LA “LUED”
Al tiempo propio de ese observador rápido distante del objeto masivo y que está ubicado fuera del campo gravitacional, ese mismo tiempo propio debe ser un tiempo invariante pues a ese mismo observador le corresponde también una respectiva masa propia e invariante. Entonces aplicamos la “LUED” a la masa de la siguiente manera:
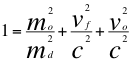 (28)
(28) 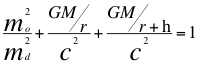 (28)
(28)
Donde mo es la masa invariante para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, md es la masa lenta para un observador lento dentro del campo gravitacional, vf es la velocidad de rotación de la fuente masiva, vo es la velocidad de rotación del observador lento ubicado dentro del campo gravitacional, G es la constante de gravitación universal, M es la masa de la fuente masiva de ondas gravitatorias, r es el radio de la fuente masiva y c es la velocidad de la luz.
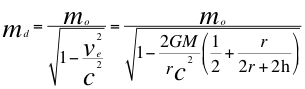 (29)
(29)
Donde mo es la masa invariante para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, md es la masa lenta para un observador lento dentro del campo gravitacional, ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente masiva de ondas gravitatorias, r es el radio de la fuente masiva, h es la altura donde se encuentra ubicado el observador lento dentro del campo gravitacional y c es la velocidad de la luz.
Cuando el observador lento que está dentro del campo gravitacional, está ubicado precisamente en la superficie del objeto masivo, la masa para ese observador lento es la siguiente:
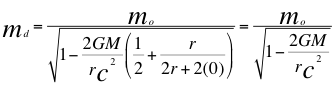 (30)
(30)
Donde mo es la masa invariante para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, md es la masa lenta para un observador lento ubicado dentro del campo gravitacional, ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente masiva de ondas gravitatorias, r es el radio de la fuente masiva y c es la velocidad de la luz.
3. CONCLUSIONES.
a)- La GRAN CONCLUSIÓN de este trabajo es que la velocidad de escape siendo un concepto puramente del Doppler transversal, es la suma como vector de la velocidad de la fuente y la velocidad del observador lento y que además, en la dilatación gravitacional del tiempo la velocidad de escape va decreciendo hasta un límite a medida que el observador lento se aleja de la fuente o cuerpo másico.
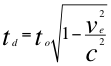 (16)
(16)
Donde td es el tiempo propio para un observador lento dentro del campo gravitacional, to es el tiempo propio para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, ve es la velocidad del escape de la fuente de ondas gravitatorias y c es la velocidad de la luz.
b)- Otra GRAN CONCLUSIÓN es encontrar el límite del valor hasta donde puede decrecer la velocidad de escape a medida que se incrementa la altura del observador lento que está dentro del campo gravitacional del cuerpo másico, tanto que cuando h=∞ sucede lo siguiente:
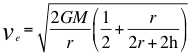 (23)
(23)
Donde ve es la velocidad de escape de una fuente de ondas gravitacionales, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo másico, r es el radio del objeto masivo, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional.
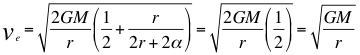 (31)
(31)
Donde ve es la velocidad de escape de una fuente de ondas gravitacionales, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo másico, r es el radio del objeto masivo, h es la altura donde está ubicado el observador lento que está dentro del campo gravitacional.
c)- Otra GRAN CONCLUSIÓN es que la masa aparente de una partícula cualquiera en la relatividad especial, si la partícula está inmersa en un campo gravitacional entonces esa masa aparente queda descrita de la siguiente manera:
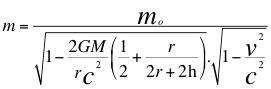 (32)
(32)
Donde m es la masa aparente de la relatividad especial dentro de un campo gravitacional, mo es la masa invariante para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, v es la velocidad de la partícula que se mueve dentro del campo gravitatorio, G es la constante de gravitación universal, M es la masa de la fuente masiva que emite ondas gravitatorias, h es la altura del cuerpo másico donde se encuentra transitando la partícula, r es el radio de la fuente masiva y c es la velocidad de la luz.
d)- Otra GRAN CONCLUSIÓN es el cálculo de la velocidad de escape en los agujeros negros quien sería igual a la velocidad de la onda gravitatoria del Doppler transversal gravitatorio:
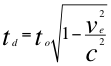 (16)
(16) 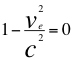 (33)
(33)
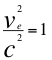 (34)
(34) ![]() (35)
(35) ![]() (36)
(36)
Donde to es el tiempo propio para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, td es el tiempo propio para un observador lento dentro del campo gravitacional, ve es la velocidad de escape y c la velocidad de la luz.
e)- Otra GRAN CONCLUSIÓN es la explicación de que el fin último que sufre la masa de una partícula que cae en un agujero negro siguiendo una geodésica que acaba en una “Singularidad” espaciotemporal, pues la masa de esa partícula se incrementaría infinitamente y ser Masa Imaginaria:
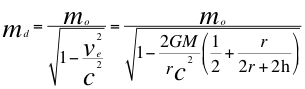 (29)
(29)
Donde mo es la masa invariante para un observador rápido distante del objeto masivo y por fuera del campo gravitacional, md es la masa lenta para un observador lento dentro del campo gravitacional, ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente masiva de ondas gravitatorias, r es el radio de la fuente masiva, h es la altura donde se encuentra ubicado el observador lento dentro del campo gravitacional y c es la velocidad de la luz.
f)- La otra GRAN CONCLUSIÓN de este trabajo es la descripción de la naturaleza física de las singularidades que son las configuraciones de un Doppler transversal límite cuando la velocidad de escape es el límite si iguala a la velocidad de la luz quien identifica a la superficie imaginaria, esférica y cerrada de altura h región del campo alrededor de un agujero negro que es como aquel sitio del espacio-tiempo circunscrito por una superficie frontera imaginaria llamada horizonte de sucesos:
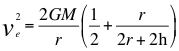 (22)
(22) 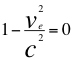 (33)
(33)
![]() (35)
(35) 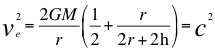 (37)
(37)
Donde ve es la velocidad de escape, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitacionales, r es el radio de la fuente de ondas gravitacionales o cuerpo másico, h es la altura a donde se sitúa la hipersuperficie imaginaria frontera de forma esférica del horizonte de sucesos que rodea la superficie del agujero negro y c la velocidad de la luz.
Por ejemplo si el horizonte de sucesos de un agujero negro estuviera a la altura de h=0 entonces la superficie esférica de la frontera imaginaria del horizontes de eventos alrededor del agujero negro coincidiera con la misma superficie material del propio agujero negro.
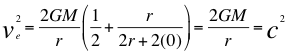 (38)
(38)
Donde ve es la velocidad de escape de una fuente de ondas gravitacionales, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo másico, r es el radio del objeto masivo, c es la velocidad de la luz.
Pero si la superficie esférica e imaginaria del horizonte de eventos alrededor de un agujero negro, se situara a cierta altura sobre la superficie material del agujero por ejemplo a una altura igual al preciso radio del mismo agujero negro donde h=r quedaría una región del espacio-tiempo por encima de la superficie material del agujero negro circunscrita entre la superficie material del agujero negro y el horizonte de eventos, entonces en la propia superficie material del agujero negro se necesitarían velocidades superiores a la de la luz para poder escapar de la superficie material del agujero negro y la teoría indica que nada puede alcanzarla, velocidad que sin embargo si es apenas suficiente en la superficie del horizonte de sucesos pero, no es competente para poder escapar de la propia superficie material del agujero negro:
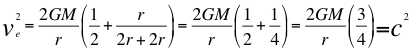 (39)
(39)
Donde ve es la velocidad de escape de una fuente de ondas gravitacionales, G es la constante de gravitación universal, M es la masa de la fuente de ondas gravitatorias o cuerpo másico, r es el radio del objeto masivo, c es la velocidad de la luz.
G)- Otra ULTIMA Y GRAN CONCLUSIÓN y quizás la más compleja e importante es lo que influyen las leyes de estas ciencias básicas en la naturaleza de la conciencia humana, pues para valorar el presente ya sea para aceptarlo o no, siendo todo absolutamente de naturaleza ondulatoria, es diferente a lo que hacemos sin embargo por lo general valoramos el instante que acontece si las cosas están bien o mal, que lo valoramos a través de una teoría de la información fuertemente determinista, y con ella elaboramos la memoria y el aprendizaje.
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[01] La masa aparente es un Doppler de la masa invariante
[02] Ondas gravitacionales y los agujeros negros
[03] corrimiento al rojo gravitacional
[04] efecto Doppler relativista
[05] corrimiento al rojo
[06] corrimiento al rojo gravitacional
[07] efecto doppler relativista
[08] efecto doppler relativista
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.