Inflación Cuántica

Inflation Quantum

Por Heber Gabriel Pico Jiménez MD

Resumen

A través de la contracción cuántica del tiempo, se logra hallar una ecuación de la energía orbital del  electrón, que para su total solución requiere la contribuición de 4 números cuánticos incluyendo al espín, con el tiempo contraído de esa manera por la presencia cuántica de energía o materia, se alcanza de paso demostrar teóricamente, la observación fenomenológica de Balmer y la constante Rydberg. Además se logra demostrar con esta base que en realidad, el ángulo que describe el electrón en su momento angular, está muy lejos de ser recto ni siquiera en el hidrogeno que es de 45 grados y no de 90 grados tal como lo había presumido Bohr.  

Palabras claves: Electrón, Orbital electrónico.

Abstract

Through the quantum time contraction, manages to find an equation of the orbital energy of the electron, that your total solution requires the values of 4 quantum numbers including the spin, eventually collapsed due to quantum energy or matter is reached step demonstrate theoretically the phenomenological observation of Balmer and the Rydberg constant. Also manages to demonstrate with this base that actually the angle which describes the electron with the orbital radius, is not be straight even on the hydrogen such as Bohr had hypothesized it.

Keywords: Electron, Orbital Electronic.

1. Introducción

Se cree que los procesos físicos a nivel microscópico son en su mayor parte temporalmente simétricos. Además ciertas interacciones en el plano subatómico implican que la fuerza nuclear débil viola la conservación de la paridad, aunque solo muy raramente. De acuerdo con el teorema de la simetría CPT (Simetría fundamental de las leyes físicas en el entorno de transformaciones que involucran las inversiones de la carga, paridad y tiempo simultáneamente), esto significa que el tiempo podría ser reversible. Este ordenamiento del tiempo, no está relacionado con ningún otro mecanismo, lo que podría sugerir que nuestro universo debía estar hecho de antimateria en lugar de materia. De acuerdo con la interpretación de Copenhague de la mecánica cuántica, la evolución cuántica se halla gobernada por la ecuación de Schrödinger, que es temporalmente simétrica y por el colapso de la función de onda, que es irreversible en el tiempo. Dado que el mecanismo del colapso de la función de onda es todavía oscuro, no se conoce como se pueden vincular a estas dos evoluciones temporales.   

Se dice que en mecánica cuántica el proceso de medición altera de forma incontrolada la evolución del sistema, además que sea un error pensar que medir es revelar propiedades que estaban en el sistema con anterioridad. La información que nos proporciona la función de onda es la distribución de probabilidades, con la cual se podrá medir tal valor de tal cantidad. Cuando medimos ponemos en marcha un proceso que es indeterminable a priori, lo que algunos denominan azar, ya que habrá distintas probabilidades de medir distintos resultados. La función de onda nos informa de cuáles son los resultados posibles de una medida y sus probabilidades relativas, pero no nos dice que resultado concreto se obtendrá si un observador trata efectivamente de medir el sistema o averiguar algo sobre él, es decir, la medida sobre un sistema aparece como un valor impredecible de entre los resultados posibles.

La gravedad mirándola como fuerza, jamás podrá producir orbitas cerradas de formas repulsivas pero, si ellas son tratadas como una deformación de la geometría del espacio-tiempo, por efectos de la cantidad de masa, si es posible. El espacio y el tiempo asumen un papel dinámico. Así la masa cuántica deforma al espacio-tiempo de su entorno, de manera que el propio espacio-tiempo empuje los cuerpos hacia afuera.

Las partículas se desintegran por la acción de procesos cuánticos y por ello, hay presente un elemento de impredectibilidad. Lo que si puede determinarse es el tiempo necesario para que una población idéntica se reduzca a la mitad (periodo de semidesintegración). Se define vida media como el tiempo que tarda una muestra en convertirse en 1/e de su tamaño original (donde e es el número base de los logaritmos neperianos). Se sabe que la vida media del protón es mayor de 1030 años y que la vida media del electrón es mayor de 1021 años; por ello decimos que estas dos partículas son estables, pues su vida media es en muchos órdenes de magnitud más grande que la vida del Universo, que aproximadamente se calcula en unos 1010 años.

Al ser los protones los  bariones   más ligeros, la conservación del número bariónico nos llevaría a conjeturar su estabilidad. De hecho, la desintegración espontánea de los protones libres nunca ha sido observada. Sin embargo, algunas teorías que no conservan el número bariónico, entre las que se encuentran las teorías de la gran unificación, predicen procesos del tipo:

p → e⁺ + π⁰
p → μ + π⁰

Donde un protón se desintegraría hipotéticamente, en un positrón y en un pión neutro; o en un muon y un pión neutro.

Distintos montajes experimentales buscaron estas hipotéticas desintegraciones sin éxito en enormes cámaras subterráneas llenas de agua. El detector de partículas Super-Kamiokande en Japón, aunque no encontró ninguna de estos sucesos, estableció experimentalmente límites inferiores a la vida media de un protón del orden de 1033 años. 

2. Desarrollo del Tema.

La relación conocida de la dilatación gravitacional del tiempo de Schwarzschild.

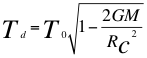(1)
Donde Td es el tiempo propio o período para el observador lento ubicado dentro del campo gravitacional, T0 es el tiempo propio o período para el observador rápido distante del objeto masivo y por tanto fuera del campo gravitacional, G es la constante gravitacional, M es la masa del cuerpo masivo, R es la coordenada radial de Schwarzschild del observador y C es la velocidad de la luz en el vacío.

Del lado asintótico externo, convexo y gravitacional de un horizonte de eventos, como superficie frontera que es del espacio-tiempo, alrededor de una determinada cantidad de masa, queda ubicada la masa y no la energía y el objeto masivo se volverá inobservable mientras tenga el respectivo radio de Schwarzschild pero, en algún momento hará nuevamente su aparición al observador si aumenta su radio o disminuye su masa. El período de tiempo para un observador distante será más extenso que para uno de la superficie.

Pero asintóticamente del otro lado del respectivo horizonte de eventos es decir, del lado cóncavo correspondiente al agujero negro, queda ubicada es la energía del cuerpo masivo.

El tiempo cuántico es el llamado tiempo subatómico para un observador atómico.

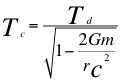(2)
Donde Tc es el tiempo propio período para el observador rápido cuántico ubicado dentro del sistema cuántico, Tdes el tiempo propio o período para el observador lento ubicado distante y por tanto fuera del sistema cuántico, G es la constante gravitacional, m es la masa nuclear atómica, res la coordenada radial cuántica del observador cuántico y C es la velocidad de la luz en el vacío.

Reemplazamos ahora el tiempo de la superficie planetaria en la relación del tiempo subatómico.

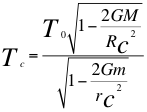(3)
Donde Tc es el tiempo propio para el observador rápido cuántico ubicado dentro del sistema cuántico, T0 es el tiempo propio para el observador rápido distante del objeto masivo y por tanto fuera del campo gravitacional, G es la constante gravitacional, M es la masa del cuerpo masivo, R es la distancia clásica desde el centro del objeto al observador, m es la masa nuclear atómica, res la coordenada radial cuántica de Schwarzschild del observador cuántico y C es la velocidad de la luz en el vacío.

En esta anterior relación, el átomo estudiado en el denominador, está ubicado en el radio del cuerpo masivo descrito en el numerador.

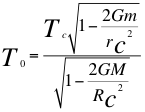(4)
Donde T0 es el tiempo propio para el observador rápido distante del objeto masivo y por tanto fuera del campo gravitacional, Tc es el tiempo propio para el observador rápido cuántico ubicado dentro del sistema cuántico, G es la constante gravitacional, M es la masa del cuerpo masivo, R es la distancia clásica desde el centro del objeto al observador, m es la masa nuclear atómica, res la coordenada radial cuántica de Schwarzschild del observador cuántico y C es la velocidad de la luz en el vacío.

Esto quiere decir que el tiempo en el universo depende del equilibrio entre el tiempo cuántico y tiempo gravitacional. Por eso decimos que el tiempo del observador lento dentro del campo gravitacional es:

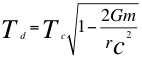(5)
Donde Tdes el tiempo propio o período para el observador lento ubicado distante y por tanto fuera del sistema cuántico, Tc es el tiempo propio para el observador rápido cuántico ubicado dentro del sistema cuántico, G es la constante gravitacional, m es la masa nuclear atómica, res la coordenada radial cuántica del observador cuántico y C es la velocidad de la luz en el vacío.

En la interacción con un electrón de un sistema ¿con cuál tiempo se trabaja en la función de onda? Pues utiliza el tiempo del respectivo sistema o el del observador inercial ubicado dentro del campo gravitacional. Si bien es cierto que la conciencia del observador puede involucrarse limpiamente en el sistema al momento de la medida, se rompe la pulcritud de la relación.

Mecánica Cuántica

Bien, ahora vamos a iniciar la prueba de lo expuesto anteriormente, desarrollando el momento angular del electrón en el segundo postulado de Bohr, quien además reza que no todas las orbitas están permitidas, solo se pueden hacer en orbitas cuyo radio cumpla con el momento angular del electrón y que sea un múltiplo entero de ħ la constante reducida de Planck:

(6)
Donde me es la masa del electrón, v es la velocidad del electrón, r es el radio de la órbita, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número entero y ħ es la constante reducida de Planck.

Bien, ahora vamos a corregir el tiempo en la constante de Planck y en la velocidad del electrón en el segundo postulado de Bohr, donde estamos de acuerdo de que el momento angular debe cumplir un número enteros de energía en constantes de Planck:

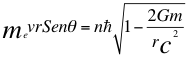(7)
Donde m_e es la masa del electrón, v es la velocidad del electrón, r es el radio de la órbita, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número entero, ħ es la constante reducida de Planck, G es la constante gravitacional, m es la masa nuclear atómica y C es la velocidad de la luz en el vacío.

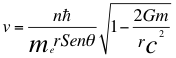(8)
Donde m_e es la masa del electrón, v es la velocidad del electrón, r es el radio de la órbita, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número entero, ħ es la constante reducida de Planck, G es la constante gravitacional, m es la masa nuclear atómica y C es la velocidad de la luz en el vacío.

Comenzamos a trabajar ahora en el primer postulado de Bohr donde se consigue un equilibrio orbital en el electrón, entre la fuerza coulombiana atractiva por la presencia del núcleo y la fuerza centrifuga:

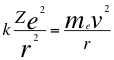(9)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, ves la velocidad del electrón y r es el radio de la órbita.

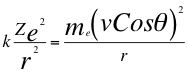(10)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, ves la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

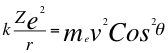(11)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, ves la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

Ahora introducimos en la anterior relación, la corrección en el tiempo cuántico de la constante de Coulomb:

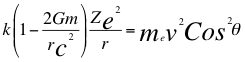(12)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, ves la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

Ahora a la velocidad del electrón en la anterior relación número ocho la reemplazamos en la también anterior número doce (12), ecuación del primer postulado de Bohr corrigiéndole también el tiempo tanto a la constante de Coulomb como a la constante reducida de Planck:

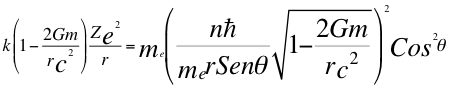(13)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, n es un número entero, ħ es la constante reducida de Planck, G es la constante de gravitación, m es la masa del átomo, C es la velocidad de la luz en el vacío, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

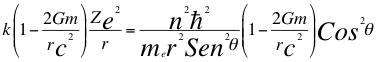(14)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, n es un número entero, ħ es la constante reducida de Planck, G es la constante de gravitación, m es la masa del átomo, C es la velocidad de la luz en el vacío, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

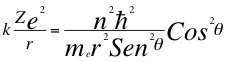(15)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, n es un número entero, ħ es la constante reducida de Planck, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

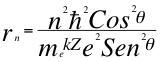(16)
Donde r es el radio de la órbita, n es un número entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

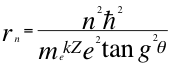(17)
Donde r es el radio de la órbita, n es un número entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

Aquí en este momento de acuerdo a la cuántización del radio se define el tipo de orbital, porque en el primer nivel del hidrogeno el ángulo es de 45 grados y no 90 grados, tal como lo había presumido Bohr, entonces la tangente es igual a uno (1) y el radio de Bohr es igual:

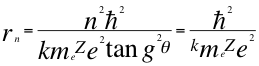(18)
Donde r es el radio de la órbita, n es un número entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

Es decir que todos los orbitales S tienen el mismo angulo de 45 grados. A medida que disminuye el ángulo teta, aumenta el radio es decir el radio esta cuantizado.

Ahora vamos a aplicar la relatividad en la anterior relación del momento angular número siete (7):

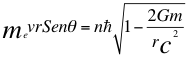(7)
Donde m_e es la masa del electrón, r es el radio de la órbita, v es la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número entero, ħ es la constante reducida de Planck, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

(18a)
Donde v es la velocidad del electrón, n es un número entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, r es el radio de la órbita, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

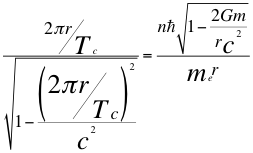(19)
Donde r es el radio de la órbita, Tc es el periodo cuántico del electrón, n es un número entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

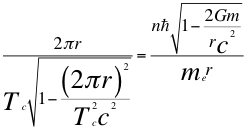(20)
Donde r es el radio de la órbita, Tc  es el periodo cuántico del electrón, n es un número entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, G es la constante de gravitación, m es la masa del átomo, C es la velocidad de la luz en el vacío y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

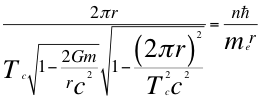(21)
Donde r es el radio de la órbita, Tc es el periodo cuántico del electrón, n es un número entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, G es la constante de gravitación, m es la masa del átomo, C es la velocidad de la luz en el vacío y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

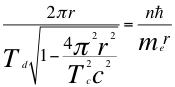(22)
Donde r es el radio de la órbita, n es un número entero, ħ es la constante reducida de Planck, Td es el tiempo propio o período para el observador lento ubicado dentro del campo gravitacional, Tc es el período cuántico del electrón, m_e es la masa del electrón y C es la velocidad de la luz en el vacío.

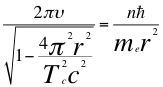(23)
Donde υ es la frecuencia del electrón, n es un número entero, ħ es la constante reducida de Planck, Tc es el periodo cuántico del electrón, m_e es la masa del electrón, r es el radio de la órbita y C es la velocidad de la luz en el vacío.

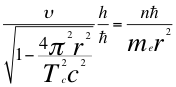(24)
Donde υ es la frecuencia del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck, Tc es el periodo cuántico del electrón, m_e es la masa del electrón, r es el radio de la órbita y C es la velocidad de la luz en el vacío.

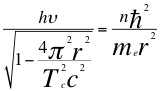(25)
Donde h es la constante de Planck, υ es la frecuencia del electrón, n es un número entero, ħ es la constante reducida de Planck, Tc es el periodo cuántico del electrón, m_e es la masa del electrón, r es el radio de la órbita y C es la velocidad de la luz en el vacío.

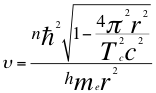(26)
Donde h es la constante de Planck, υ es la frecuencia del electrón, n es un número entero, ħ es la constante reducida de Planck, Tc es el periodo cuántico del electrón, m_e es la masa del electrón, r es el radio de la órbita y C es la velocidad de la luz en el vacío.

Aunque se respeta la sustitución del radio del electrón y el período en el interior del radical, se hace en el resto de la anterior relación número (25) y encontramos la siguiente ecuación:

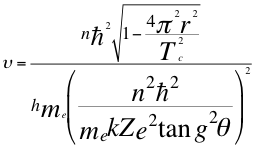(27)
Donde h es la constante de Planck, υ es la frecuencia del electrón, n es un número entero, ħ es la constante reducida de Planck, r es el radio de la órbita, Tc es el periodo cuántico del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, C es la velocidad de la luz en el vacío y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

Seguimos Reemplazando

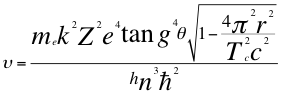(28)
Donde υ es la frecuencia del electrón, h es la constante de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número entero y ħ es la constante reducida de Planck.

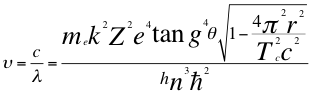(29)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, h es la constante de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número entero y ħ es la constante reducida de Planck.

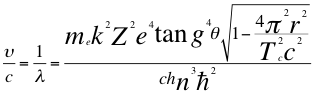(30)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo donde se encuentra el electrón, e es la carga del electrón, r es el radio de la órbita del electrón, Tc es el período cuántico del electrón, C es la velocidad de la luz en el vacío, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número entero y ħ es la constante reducida de Planck.

Segundo Número Cuántico

En el cálculo de la energía fundamental del hidrogeno el producto de la tangente del ángulo teta (θ) que sabemos es igual 45 grados, elevada a la cuatro por el factor de dilatación de la frecuencia descrito en la anterior relación, es igual a n½ que representaría de manera resumida en el hidrogeno, al segundo número cuántico.

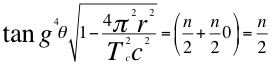(31)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío y n es un número entero.

Por eso en la explicación teórica que hace Bohr de la prueba fenomenológica de Balmer, donde cambia el número cuántico principal pero, sigue siendo un orbital de la misma forma nítida del anterior que obedece al número cuántico principal.

Ahora reemplazamos a la anterior relación número 31 del número cuántico en la también anterior relación de la energía del electrón número 30:

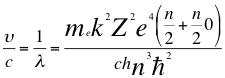(32)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

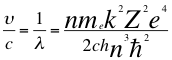(33)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

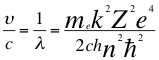(34)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

Esto es lo que nos lleva a generalizar este comportamiento en la formulación del segundo número cuántico para pares de electrones teniendo en cuenta al espín del electrón.

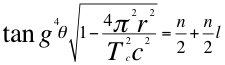(35)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío, l es el segundo número entero cuántico y n es el primer número cuántico entero.

Entonces en el hidrogeno y cualquier orbital S que tenga la misma forma nítida, l=0 y por eso es que el valor del segundo número cuántico queda de la siguiente manera:

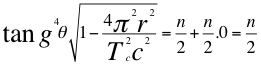(36)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío, l es el segundo número entero cuántico y n es el primer número cuántico entero.

En un orbital que tenga la forma achatada o principal P, el segundo número cuántico entero es l=1:

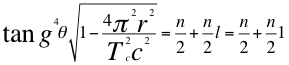(37)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío, l es el segundo número entero cuántico y n es el primer número cuántico entero.

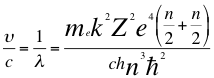(38)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

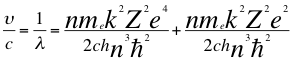(39)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

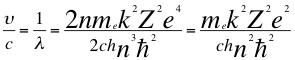(40)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

En un orbital que tenga la forma lobar o difusa de d, el segundo número cuántico entero es l=2:

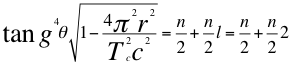(41)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío, l es el segundo número entero cuántico y n es el primer número cuántico entero.

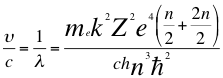(42)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

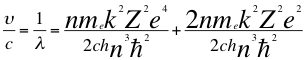(43)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

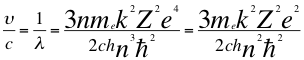(44)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número entero, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

3- Conclusiones:

-La primera conclusión es la observación de que esta anterior relación número 30, se puede resolver y entender de forma exacta si tenemos en cuenta las direcciones y orientaciones espaciales de los valores de los 4 números cuánticos incluyendo al espín, dicha ecuación impone en la lógica espacial, una serie de restricciones que se identifican en una serie de 4 números cuánticos. Vemos demasiado interesante el hecho de poder deducir de paso a la constante de Rydberg a partir de la mecánica relativista y la dilatación cuántica del tiempo, sin recurrir a la formula de la energía total del electrón en órbita de la mecánica clásica. Vemos que la orientación y forma espacial del orbital enfrente a un campo magnético exógeno, expresa en el tercer número cuántico, la forma como el ángulo θ se orienta llevando un valor implícito en el segundo número cuántico de la ecuación.

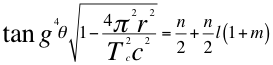(45)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío, n es el primer número cuántico, l es el segundo número cuántico del electrón o del momento angular o azimutal y m es el tercer número cuántico de esta relación.

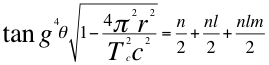(46)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, Tc es el periodo cuántico del electrón, C es la velocidad de la luz en el vacío n es el primer número cuántico entero, l es el segundo número cuántico del electrón, m es el tercer número cuántico de esta relación.

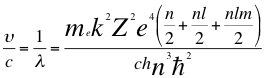(47)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es el primer número cuántico entero, l es el segundo número cuántico del electrón, m es el tercer número cuántico de esta relación, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

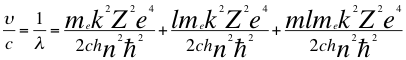(48)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es el primer número cuántico entero, l es el segundo número entero cuántico del electrón, m es el tercer número entero cuántico del electrón en esta relación, ħ es la constante reducida de Planck y C es la velocidad de la luz en el vacío.

Los valores que pueden tomar los números cuánticos para describir la energía de un electrón, el primer número cuántico entero (n), puede tomar valores enteros que van desde uno hasta el infinito. El segundo número cuántico (l) o del momento angular, puede tomar valores que van desde cero hasta n-1. El tercer número cuántico entero (m) que cumpliría los requisitos de esta ecuación además puede tomar valores enteros desde cero, hasta un número equivalente a la mitad del número máximo de electrones que quepan en el segundo número cuantico o respectivo subnivel l/2. En la solución de esta ecuación se asume al espín como el cuarto número cuántico de espín para completar las expectativas de que en cada subnivel se completen dos electrones de espin opuestos.

4- Referencias

[1]    Orbital Atómico.
[2]    Números Cuánticos.
[3]    Átomo de Bohr.
[4]    Líneas de Balmer.
[5]    Constante Rydberg.
[6]    Dilatación gravitacional del tiempo.
[7]    Número Cuántico magnético.

© heberpico@hotmail.com todos los derechos reservados.