Números Cuánticos en Momento Angular del Electrón

Quantum numbers in Angular moment of the Electron

Por Heber Gabriel Pico Jiménez MD

Resumen

En este artículo los número cuánticos del electrón quedan representados todos en su momento angular además se demuestra que en realidad, el tradicional primer número cuántico entero a que se refirió Bohr en el hidrogeno, no bastaba para expresar solo el equilibrio en la cuantificación total de la energía del momento angular del electrón en átomos distintos al hidrogeno, solo un número que expresara íntegramente la relación matemática incluso no entera, entre los 4 números cuánticos ellos si enteros, alcanza a conseguir la descripción total de los procesos ocurridos en el momento angular de la partícula. Además este artículo postula la mecánica de como el tercer número cuántico, determinaría la energía de los distintos orbitales que conforman los subniveles de energía.

Palabras claves: Electrón, Orbital electrónico.

Abstract

In this article the quantum number of the electron are represented in its angular momentum also demonstrates that in reality, the traditional first integer quantum referred to which Bohr in the hydrogen, it was not enough to express only the balance on the overall quantification of the energy of the angular momentum of the electrons in different atoms to the hydrogen, only a number that fully express the mathematical relationship even not whole, between 4 quantum numbers them if whole, reaches to get the full description of the processes occurring in the angular momentum of the particle. In addition this article postulates the mechanics of as third quantum number, would determine the power of the various orbitals that comprise the sublevels of energy.

Keywords: Electron, Orbital Electronic.

1. Introducción

En base a los artículos de Inflación cuántica1,2 publicados recientemente, en donde se demuestra que el tiempo se contrae a medida que el radio del átomo se reduce. Este postulado concuerda con la expansión del universo, con el problema de la medida en la mecánica cuántica

2. Desarrollo del Tema.

En base a los artículos de Inflación cuántica1,2 publicados recientemente, en donde se demuestra que el tiempo se contrae a medida que el radio del átomo se reduce. Este postulado concuerda con la expansión del universo,

Mecánica Cuántica

Bien, ahora vamos a iniciar la prueba de lo expuesto anteriormente, desarrollando el momento angular del electrón en el segundo postulado de Bohr, quien además reza que no todas las orbitas están permitidas, solo se pueden hacer en orbitas cuyo radio cumpla con el momento angular del electrón y que sea un múltiplo entero de ħ la constante reducida de Planck:

(1)
Donde m_e es la masa del electrón, v es la velocidad del electrón, r es el radio de la órbita, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero y ħ es la constante reducida de Planck.

Bien, ahora vamos a corregir el tiempo en la constante de Planck y en la velocidad del electrón en el segundo postulado de Bohr, donde estamos de acuerdo de que el momento angular debe cumplir un número enteros de energía en constantes de Planck:

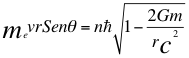(2)
Donde m_e es la masa del electrón, v es la velocidad del electrón, r es el radio de la órbita, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, G es la constante gravitacional, m es la masa nuclear atómica y C es la velocidad de la luz en el vacío.

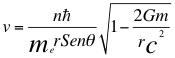
Donde v es la velocidad del electrón, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, r es el radio de la órbita, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, G es la constante gravitacional, m es la masa nuclear atómica y C es la velocidad de la luz en el vacío.

Comenzamos a trabajar ahora en el primer postulado de Bohr donde se consigue un equilibrio orbital en el electrón, entre la fuerza coulombiana atractiva por la presencia del núcleo y la fuerza centrifuga:

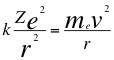(4)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, r es el radio de la órbita, m_e es la masa del electrón y ves la velocidad del electrón.

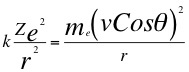(5)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, r es el radio de la órbita, m_e es la masa del electrón, ves la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

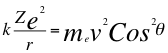(6)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, r es el radio de la órbita m_e es la masa del electrón, ves la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

Ahora introducimos la corrección en el tiempo cuántico en la anterior relación número 6 de la constante de Coulomb:

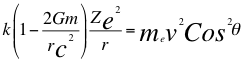(7)
Donde k es la constante de la fuerza de Coulomb, G es la constante gravitacional, m es la masa nuclear atómica, C es la velocidad de la luz en el vacío, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, ves la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

Ahora, a la velocidad del electrón en la anterior relación número 3, la reemplazamos en la anterior relación número 7 en la ecuación del primer postulado de Bohr corrigiéndole también el tiempo tanto a la constante de Coulomb como a la constante reducida de Planck:

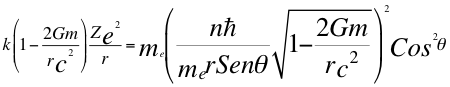(8)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, G es la constante de gravitación, m es la masa del átomo, C es la velocidad de la luz en el vacío, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

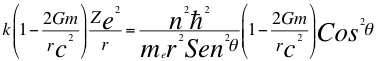(9)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, G es la constante de gravitación, m es la masa del átomo, C es la velocidad de la luz en el vacío, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

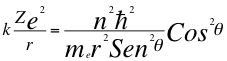(10)
Donde k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, m_e es la masa del electrón, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y r es el radio de la órbita.

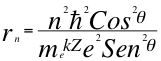(11)
Donde r es el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

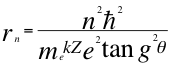(12)
Donde r es el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

Ahora vamos a seguir trabajando en la anterior relación número dos (2) del momento angular:

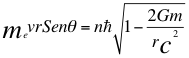(2)
Donde m_e es la masa del electrón, r es el radio de la órbita, v es la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

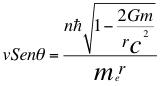(13)
Donde v es la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

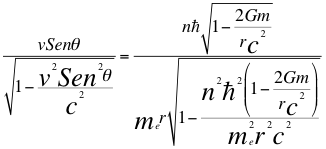(14)
Donde v es la velocidad del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

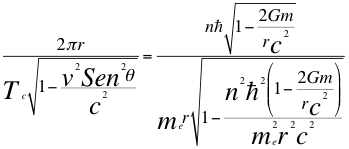(15)
Donde r es el radio de la órbita, Tc  es el periodo cuántico del electrón, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, G es la constante de gravitación, m es la masa del átomo, C es la velocidad de la luz en el vacío y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

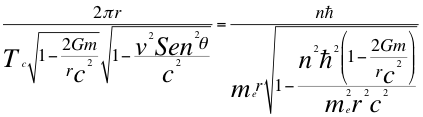(16)
Donde r es el radio de la órbita, Tc es el periodo cuántico del electrón, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, G es la constante de gravitación, m es la masa del átomo, C es la velocidad de la luz en el vacío y θ es el ángulo entre la cantidad de movimiento y el radio de la órbita.

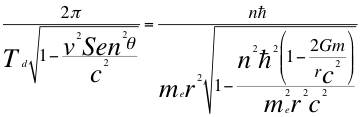(17)
Donde r es el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, Td es el tiempo propio o período para el observador lento ubicado dentro del campo gravitacional, m_e es la masa del electrón G es la constante de gravitación, m es la masa del átomo, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y C es la velocidad de la luz en el vacío.

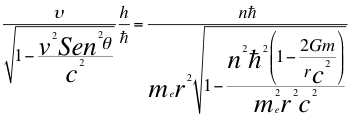(18)
Donde υ es la frecuencia del electrón, h es la constante de Planck, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y C es la velocidad de la luz en el vacío.

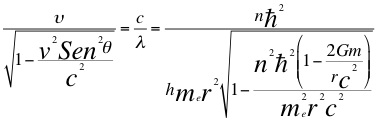(19)
Donde υ es la frecuencia del electrón, λ es la longitud de onda del electrón, h es la constante de Planck, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita y C es la velocidad de la luz en el vacío.

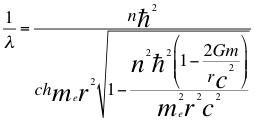(20)
Donde λ es la longitud de onda del electrón, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, h es la constante de Planck, m_e es la masa del electrón, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

Aunque se respeta la sustitución del radio orbital de la anterior relación 12 del electrón en el interior del radical, pero se hace en el resto de la anterior relación número (20) y encontramos la siguiente ecuación:

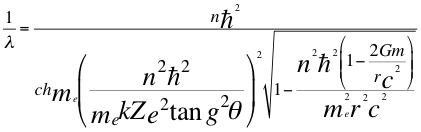(21)
Donde λ es la longitud de onda del electrón, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, h es la constante de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

Seguimos Reemplazando

Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, h es la constante de Planck, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

Números Cuánticos

Primer Número Cuántico

El primer número cuántico divide por niveles al radio de todo el átomo. A pesar de que según este trabajo todos los números cuánticos indican la distancia radial entre el núcleo y el electrón representado en niveles energéticos, los valores del primer número cuántico corresponden al primer nivel energético más influyente. Los valores de este número varían entre 1 y el infinito. El primer número cuántico entero históricamente ha sido considerado como el único responsable de sostener a todo el peso del momento angular, tal como sí coincide en el hidrogeno pero quizás es el único donde eso se presenta.

En el cálculo de la energía fundamental del electrón la relación de la tangente del ángulo teta (θ) elevada a la cuatro, entre el factor de dilatación de la velocidad orbital del electrón, es igual a n/2 que representaría de manera resumida en el hidrogeno o cualquier átomo a los número cuánticos. Pero esta n no es individualmente el primero, el segundo, el tercero ni el cuarto número cuántico, esta n es un número que resulta de la relación matemática del momento angular del electrón por los cuatro números cuánticos.

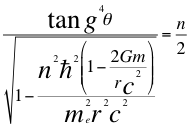(23)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

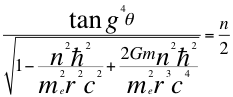(24)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

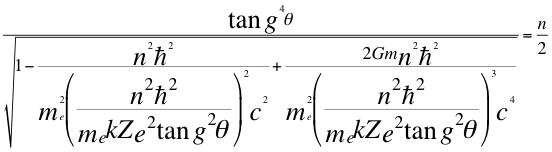(25)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

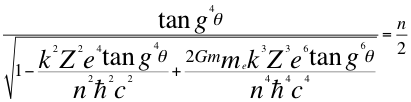(26)
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

Reemplazando la anterior relación 26 en la también anterior relación 22, nos quedaría la siguiente:

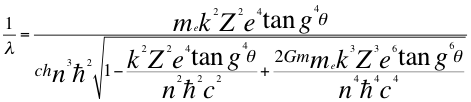(27)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, h es la constante de Planck, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

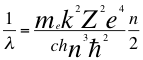(28)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

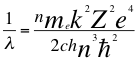(29)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

Por eso en la explicación teórica que hace Bohr de la prueba fenomenológica de Balmer, donde cambia el número cuántico principal, pero sigue siendo un orbital de la misma forma nítida del anterior que obedeció al número cuántico inicial.

Podríamos decir que el primer número cuántico es la parte entera del número total que equilibra el momento angular del electrón, porque si en el hidrogeno coincide el número del momento angular del electrón ser el mismo primer número cuántico entero, en los electrones de otros átomos no sucede lo mismo por eso lo denotamos como n1 al primer número cuántico.

Segundo Número Cuántico

De cada nivel que previamente dimensiona e identifica n₁como primer número cuántico, de manera interna, un segundo número cuántico se encarga de medirlo cuánticamente. A pesar de que este número indica la forma del orbital, en este trabajo también corresponde a la cantidad de energía del respectivo subnivel donde orbita el electrón. Los valores de este segundo número varían desde 0 hasta el valor que le permita el primer nivel que menos uno (n₁-1). No decimos n-1 para que no corra el riesgo de confundirlo con el n representa con el del momento angular n que es el número total que representaría relacionados a todos los niveles y subniveles energéticos del momento angular del electrón y que incluso podría no ser exactamente un número entero. Partiendo de que el valor del subnivel llega hasta n1-1 y vamos a estudiar a un electrón del segundo nivel, entonces partimos de que el primer número cuántico entero es n₁=2, entonces el número máximo que puede tomar el subnivel l para ese segundo nivel es l=n₁-1=1. Es decir en el segundo nivel de energía habrían dos subniveles l, el primero que sería l=0 y que corresponde a la forma del orbital so nítida y el segundo subnivel l=1, que corresponde al orbital 2p del segundo nivel, es decir que la cantidad de energía del segundo nivel la requieren dos números cuánticos enteros.

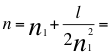(30)
Donde n es un número total que podría no ser entero y representa al conjunto de los números cuánticos que tiene el orbital del electrón, n₁es el primer número cuántico entero, l es el segundo número cuántico entero.

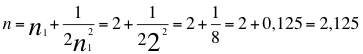(31)
Donde n es un número total que podría no ser entero y representa al conjunto de los números cuánticos que tiene el orbital del electrón, n₁es el primer número cuántico entero.

n = 2,125 (32)
Donde n es un número que podría no ser entero y representa al conjunto de los números cuánticos que tiene el orbital del electrón.

2n₁² = Electrones
Donde 2n₁² = este es el número máximo de electrones que le corresponden a un nivel n₁de energía.

Por ejemplo un electrón como el de Balmer que se encuentre orbitando en el subnivel s del segundo nivel, entonces n₁=2, l=0 y tendría la siguiente cantidad de energía:

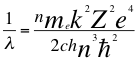(29)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es el resultado del conjuntos de todos los números cuánticos, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

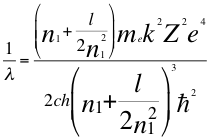(33)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

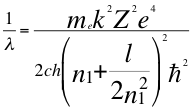(34)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

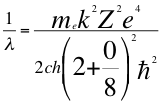(35)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

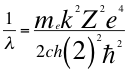(36)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

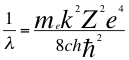(37)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

Un electrón que se encuentre esta vez orbitando un subnivel p distinto de cero en el segundo nivel, todos sabemos que el valor máximo que puede tomar l cuando n1=2, l=n1-1=2-1=1 entonces el valor máximo de p es l=1 como máximo valor de subnivel p del segundo nivel y este nivel tendría la siguiente cantidad de energía:

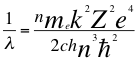(29)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n es el resultado del conjuntos de todos los números cuánticos, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

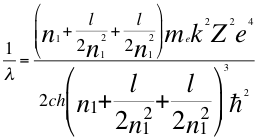(38)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

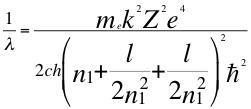(39)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

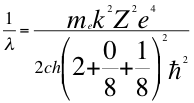(40)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

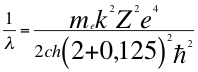(41)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

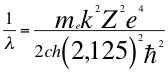(42)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

(43)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

 
Para un electrón que orbite el tercer nivel de energía, entonces sabemos que n1=3 y que ese nivel cuenta con la presencia de 3 subniveles, descritos por el segundo número cuántico. Sabemos también que a ese nivel de energía, el valor máximo del subnivel l es: l=n1-1=3-1=2. Lo que nos sugiere que el subnivel l tiene 3 orbitales que van desde l=0 hasta l=2 y aplicamos la anterior relación número 38.

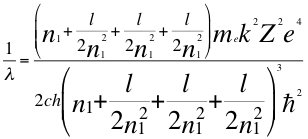(44)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

(45)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

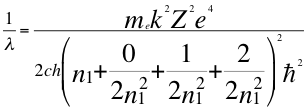(46)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

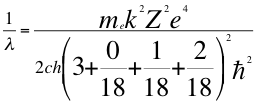(47)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

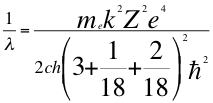(48)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

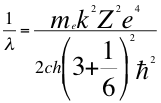(49)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

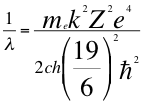(50)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

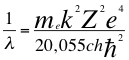(51)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

Tercer Número Cuántico.

El número cuántico magnético hasta ahora en la mecánica cuántica, solo define la orientación espacial del orbital frente a un campo magnético externo. Pero resulta que los electrones que pueblan un subnivel no lo hacen todos en el mismo orbital del respectivo subnivel, por lo tanto no están en el mismo orbital, se encuentran por pares ubicados en distintos orbitales. Es decir que cada subnivel tiene distintos valores de un tercer número cuántico. Describamos el orbital que enmarca el tercer número cuántico de un electrón en el subnivel p del segundo nivel de energía:

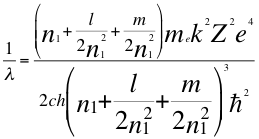(41)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

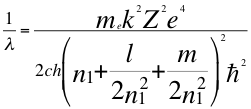(42)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

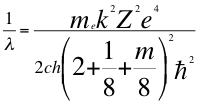(43)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

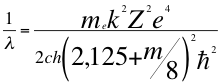(44)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

El subnivel p o l=1 tiene un máximo de 6 electrones y por lo tanto el tercer número cuánticos entero toma 3 valores, m por ejemplo, tenemos el siguiente resultado m=2l+1: por lo tanto el tercer número cuántico entero en el subnivel p, toma tres valores que los determina 2l+1: y van desde cero hasta dos o sea son 0, 1 y 2.

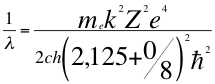(45)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

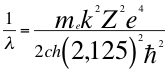(46)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

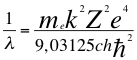(47)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

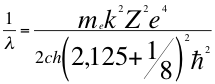(48)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

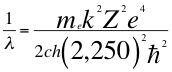(49)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

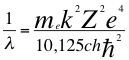(50)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

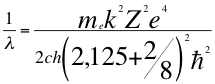(51)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

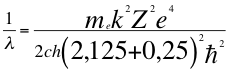(52)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

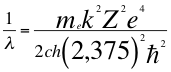(53)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

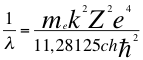(54)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

Esto es lo que nos lleva a generalizar este comportamiento en la formulación del segundo número cuántico para cada par de electrones en el mismo orbital teniendo en cuenta al espín del electrón.

3- Conclusiones:

1-La primera conclusión es la observación de que con la anterior relación número 28, se puede resolver y entender de forma exacta si tenemos en cuenta las direcciones y orientaciones espaciales de los valores de los 4 números cuánticos incluyendo al espín que no hay la necesidad de introducirlo sino que el surge de manera espontánea, dicha ecuación impone en la lógica espacial, una serie de restricciones que se identifican en una sucesión de 4 números cuánticos. Vemos demasiado interesante el hecho de poder deducir de paso a la constante de Rydberg a partir de la mecánica relativista y la dilatación cuántica del tiempo, sin tener que recurrir a la fórmula clásica de la energía total del electrón en órbita. Vemos que la orientación y forma espacial del orbital enfrente a un campo magnético exógeno, expresa en el tercer número cuántico la forma como el ángulo θ se orienta llevando un valor implícito en el segundo número cuántico de la ecuación.

2-La segunda conclusión son los valores que pueden tomar los números cuánticos para describir la energía de un electrón, el primer número cuántico entero (n1), puede tomar valores enteros que van desde uno hasta el infinito. El segundo número cuántico (l) o del momento angular, puede tomar valores que van desde cero hasta n1-1. El tercer número cuántico entero (m) que cumpliría los requisitos de esta ecuación además puede tomar valores enteros desde cero hasta completar un número de 2l+1, que van desde cero, hasta un número máximo equivalente a la mitad del número máximo de electrones que quepan en el segundo número cuántico o respectivo subnivel l/2. En la solución de esta ecuación se asume al espín como el cuarto número cuántico de espín para completar las expectativas de que en cada subnivel se completen dos electrones de espín opuestos.
3-Una tercera conclusión es la que nos entrega la anterior relación número 22, donde se puede notar que los números cuánticos dependen del cociente entre la tangente a la cuarta del ángulo del momento angular del electrón sobre la dilatación que causa la velocidad relativista de la partícula:

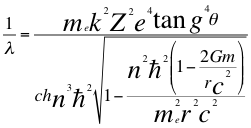
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, h es la constante de Planck, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, r es el radio de la órbita, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

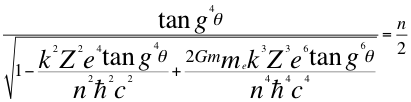
Donde θ es el ángulo entre la cantidad de movimiento y el radio de la órbita, n es un número que inicialmente se pensó que era exclusivamente entero, ħ es la constante reducida de Planck, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, G es la constante de gravitación, m es la masa del átomo y C es la velocidad de la luz en el vacío.

La dilatación causada por la velocidad del electrón con seguridad es mayor que uno, de lo contrario no existiría dilatación debida a la velocidad relativista del electrón, lo que nos sugiere que la tangente del ángulo del momento angular del electrón, podría ser menor que uno y por la tanto, el ángulo podría ser inicialmente menor de 45 grados y a medida que va aumentando el número atómico se incrementa el valor del ángulo.
 
4-Una predicción de todos estos trabajos con la contracción cuántica del tiempo, es que el ángulo del momento angular del electrón incluso en el hidrogeno, podría ser menor de 45 grados o estar muy cerca y no es 90 como lo dijo Bohr.

5-Una quinta Conclusión de este trabajo, es poder señalar al ángulo θ del momento angular del electrón, como el factor exacto que marcaría la diferencia entre el orbital de un subnivel s, p, d, f…. de un nivel y otro orbital, que aunque sea de un mismo subnivel pertenece a otro nivel del mismo átomo.

6-Como ultima conclusión describamos un en electrón utilizando los 4 números cuánticos en el tercer nivel de energía y además, expresar el momento angular del electrón involucrando a los 4 números cuánticos. Partimos que l en el tercer nivel de energía toma valores que van desde 0 hasta llegar a no-1 por eso es hasta 2.

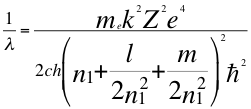(42)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

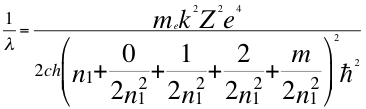(55)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

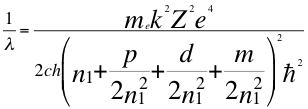(56)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, p es el segundo subnivel de energía, d es el tercer subnivel de energía, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

Resulta que el subnivel p tiene que distribuir a sus 6 electrones en 3 orbitales distintos marcados por m, el tercer número cuántico.

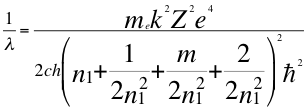(57)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

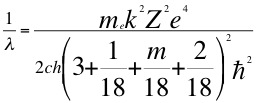(58)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

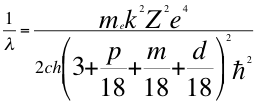(59)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, p es el segundo subnivel de energía, d es el tercer subnivel de energía, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

El subnivel p a sus 6 electrones los distribuye en 3 orbitales distintos que se los brinda m cuyos valores son 0, 1 y 2.

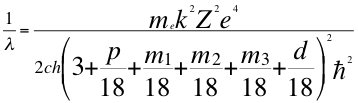(60)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, p es el segundo subnivel de energía, d es el tercer subnivel de energía, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

Pero resulta que el subnivel d también tiene su cuarto número cuántico y le corresponden 5 números m y son respectivamente 0, 1, 2, 3 y 4.

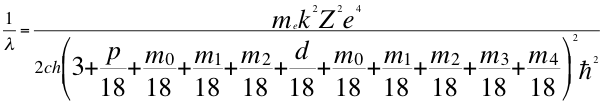(61)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, p es el segundo subnivel de energía, d es el tercer subnivel de energía, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

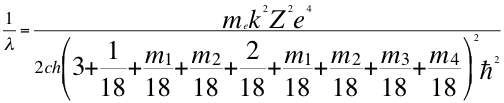(62)
Donde λ es la longitud de onda del electrón, m_e es la masa del electrón, k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón, h es la constante de Planck, n₁es el primer número cuántico entero, m es el tercer número cuántico entero, ħ es la constante reducida de Plancky C es la velocidad de la luz en el vacío.

-De acuerdo a este trabajo el momento angular del electrón quedaría descrito de la siguiente manera:

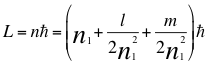(63)
Donde L es el momento angular del electrón, n es la resultante de los 4 números cuánticos en el momento angular del electrón, ħ es la constante reducida de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero y m es el tercer número cuántico entero.

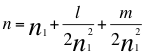(64)
Donde n es la resultante de los 4 números cuánticos en el momento angular del electrón, ħ es la constante reducida de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero y m es el tercer número cuántico entero.

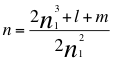(65)
Donde n es la resultante de los 4 números cuánticos en el momento angular del electrón, ħ es la constante reducida de Planck, n₁es el primer número cuántico entero, l es el segundo número cuántico entero y m es el tercer número cuántico entero.

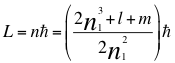(66)
Donde L es el momento angular del electrón, n es la resultante de la relación de los 4 números cuánticos en el momento angular del electrón, n₁es el primer número cuántico entero, l es el segundo número cuántico entero, m es el tercer número cuántico entero y ħ es la constante reducida de Planck.

4- Referencias

[1]    Inflación Cuántica textos científicos.
[2]    Inflación Cuántica Monografías.
[3]    Orbital Atómico
[4]    Números Cuánticos.
[5]    Átomo de Bohr.
[6]    Líneas de Balmer.
[7]    Constante Rydberg.
[8]    Dilatación gravitacional del tiempo.
[9]    Número Cuántico magnético.

Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena Colombia. Investigador independiente de problemas biofísicos médicos propios de la memoria, el aprendizaje y otros entre ellos la enfermedad de Alzheimer.
Estos trabajos han sido debidamente presentados a la “Academia Colombina de Ciencias Exactas, Físicas y naturales” ACCEFYN.