Formulación del segundo principio para ciclos irreversibles
El rendimiento de una máquina reversible que trabaja entre dos focos es mayor al de una máquina que trabaje entre los mismos focos pero de manera irreversible. Vamos a partir de este resultado para obtener la formulación matemática para procesos irreversibles.
![]()
![]() expresión para procesos irreversibles
expresión para procesos irreversibles
![]()
Consideremos una transformación cíclica que se desarrolla totalmente o en parte de forma irreversible. Si usamos el mismo artificio que en la formulación matemática del segundo principio, es decir, superponer a este ciclo que tendrá en general un número infinito de fuentes, infinitos ciclos con sólo dos fuentes, podremos obtener una solución similar.
![]()
Esta inecuación se llama desigualdad de Clasius y es la formulación del segundo principio para ciclos irreversibles. En general en un ciclo cualquiera reversible o no se cumple la expresión:
![]()
Cálculo de variaciones de entropía en procesos irreversibles
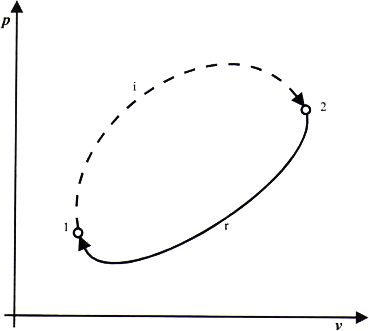
Consideremos el ciclo representado en la figura. Este ciclo está formado por dos procesos abiertos, el primero 1-2 irreversible y el segundo 2-1 reversible. A este ciclo podemos aplicar la desigualdad de Clasius.
![]()
![]()
Dado que en el proceso reversible se cumple
![]()
Tenemos
![]()
esto es cierto para cualquier proceso irreversible. En forma diferencial, se puede poner:
![]()
Recordemos que para los procesos reversibles teníamos:
![]()
Por lo tanto, para un proceso en general se cumple
![]()
En un sistema adiabático o aislado el calor transferido es nulo, por lo que la entropía solo puede crecer. Otra forma de formular el segundo principio de la termodinámica es decir que la entropía del universo siempre crece. El universo es por definición un sistema aislado.
dSuniverso ≥ 0
Esta última expresión es la que determina la espontaneidad de los procesos. Aquellos procesos que hagan aumentar la entropía del universo termodinámico, es decir, el sistema más el entorno, serán espontáneos. Los procesos en los cuales la entropía global o del universo disminuye, no podrán efectuarse en forma espontánea en la naturaleza. La experiencia demuestra, que en la naturaleza la entropía global es siempre mayor o igual que cero.