Utilizaremos los resultados obtenidos en el estudio de las máquinas térmicas para llegar a la expresión que sintetiza el segundo principio de la termodinámica. El rendimiento de la máquina de Carnot viene dado por la expresión:
![]()
Operando obtendremos
![]()
![]() bien
bien ![]()
en donde i representa el número de procesos elementales del ciclo. En el caso de un ciclo reversible distinto del ciclo de Carnot, tendremos en general un número infinito de fuentes con las que la máquina térmica intercambia calor. El ciclo reversible siempre se podrá descomponer en infinitos ciclos de Carnot infinitesimales, de tal manera que pueda considerarse que estos ciclos infinitesimales sólo intercambian calor con dos fuentes a temperatura constante. La des-composición del ciclo se muestra en la figura.
Se ha presentado un detalle en la figura siguiente, en el que se puede apreciar que la temperatura de absorción del ciclo infinitesimal de Carnot, se ha elegido de tal manera que las áreas sombreadas son idénticas. Aplicamos el primer principio al ciclo mnbam que constituye el contorno de las áreas sombreadas. Por tratarse de una evolución cíclica, la variación de energía
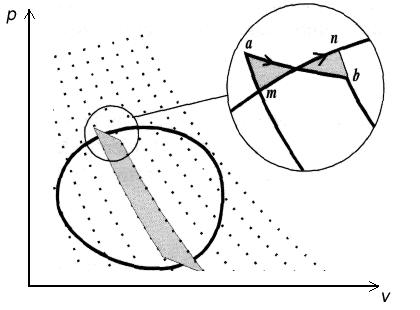
interna es cero. Como hemos elegido el ciclo de tal manera que las áreas sombreadas sean iguales y éstas se recorren en sentidos contrarios, el trabajo total del ciclo también será nulo. Esto implica que el calor absorbido en el tramo mn es el mismo que en el tramo ab.
ΔU=0; W=0 ⇔ Q = 0 = Qmn + Qba
Qmn= - Qba = Qab
Con este artificio se consigue convertir un ciclo reversible cualquiera como superposición de infinitos ciclos de Carnot. En ellos se cumplirá:
![]()
y si tenemos en cuenta los infinitos ciclos:
![]()
Esta expresión es conocida como la igualdad de Clausius y constituye la base de la formulación matemática del segundo principio, porque da pie para la definición de una nueva función de estado conocida como entropía.