Hasta ahora nos hemos ocupado principalmente de las propiedades de la entropía en cuanto función de estado. Veremos ahora otras de sus propiedades.
A diferencia de la energía, la entropía no se conserva, a pesar de ser también una función de estado. En Mecánica se suele designar sistema conservativo aquél en el cual la cantidad de trabajo necesaria para desplazar un cuerpo de una posición a otra es independiente del camino. La analogía con la Mecánica puede llevar a pensar que todas las funciones de estado se conservan, cosa que no es cierta. Que la energía interna sea una función de estado que se conserva, mientras que la entropía no se conserva, nos enseña que la analogía entre sistemas mecánicos y sistemas termodinámicos no es completa. Para apreciar mejor los alcances de dicha analogía hace falta recurrir a los métodos de la Mecánica Estadística.
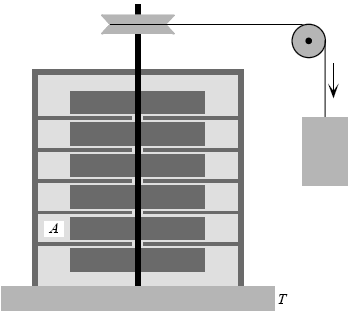
Para ilustrar la no conservación de la entropía podemos considerar el aparato de Joule, que se lo estudia en la Primera Ley. Este aparato es un ejemplo de “generador de entropía”. El experimento se puede hacer como se indica en la figura.
El fluido A que está siendo agitado en el recipiente se puede mantener a una temperatura constante T al estar en contacto con una fuente térmica a través de una pared diatérmica. A medida que giran las paletas la temperatura del fluido se mantiene constante debido a que fluye calor desde el fluido a la fuente térmica. Este flujo es reversible pues en todo instante hay sólo una diferencia infinitesimal de temperatura entre el fluido y la fuente. La variación de entropía de la fuente térmica es:
![]()
Esta es también la variación total de entropía del sistema compuesto constituido por el fluido más la fuente térmica, puesto que el estado del fluido A no ha cambiado al final del proceso. Además ΔUA = 0 de modo que QR =W, y el aumento total de entropía es:
![]()
Luego la realización continua de trabajo sobre el sistema genera continuamente entropía. Además la entropía del sistema de pesas que mueve a las paletas no cambia durante el proceso, y que la entropía generada no ha salido “de la nada”, se creó debido a la desaparición de trabajo en el ambiente. Se podría pensar que para que aumente la entropía de un sistema es necesario que éste interactúe con el ambiente (como en el ejemplo de las paletas). Esto no es cierto: la entropía de un sistema aislado puede también crecer.
Otra de las propiedades importante es que la variable entropía genera un criterio que determina el grado de espontaneidad de un proceso natural. Si en un proceso natural la entropía del sistema mas la entropía del entorno disminuye, el proceso sin lugar a dudas se realizó con ayuda exterior, es decir no fue espontáneamente. Entonces nos preguntamos: ¿Qué caracteriza a esta variable de estado, capaz de determinar el sentido de los procesos? La respuesta está relacionada con la naturaleza probabilística de la materia a nivel microscópico.

La interpretación microscópica nos ayuda a entender la dificultad de la conversión de calor en trabajo. Imaginemos un recipiente aislado como el de la figura de arriba, dotado de un ventilador por el cual podemos introducir trabajo al sistema. Al batir las palas del ventilador, transmitimos al gas una energía en forma de movimiento organizado forzado por el propio movimiento de las palas.
Este movimiento se superpone al movimiento aleatorio de las partículas caracterizado por su temperatura. El movimiento aleatorio produce choques entre las partículas que hace que éstas se desvíen de la trayectoria impuesta por el movimiento macroscópico. La turbulencia que se crea transforma el movimiento macroscópico en microscópico. El carácter aleatorio de los 20 choques hace que la transformación de calor en trabajo se realice pasando a estados de mayor probabilidad.
La transformación de calor en trabajo, es menos probable. Imaginemos que las partículas del gas están dotadas de una cierta energía cinética de su movimiento aleatorio. La probabilidad de que una partícula se mueva en una determinada dirección es bastante baja debido al gran número de direcciones en las que podría moverse la partícula. La probabilidad de que millones de partículas vayan en la misma dirección sin acción exterior es prácticamente nula. Esto explica los enunciados de Caratheodory y de Sears-Kestin, que decían que en un sistema aislado y rígido no se puede pasar a estados de menor energía interna que el inicial, a base de trans-formar energía interna en trabajo.
Entropía y procesos irreversibles
Cuando un sistema experimenta un proceso irreversible entre un estado de equilibrio inicial y un estado de equiIibrio final, la variación en la entropía del sistema puede calcularse como:
![]()
Hacemos algunas aclaraciones. ¿Por qué si estamos analizando procesos irreversibles integramos la ecuación a través de una trayectoria reversible? La razón se encuentra en que la entropía es una función de estado, por lo que su variación dependerá exclusivamente de los estados inicial y final. Si esto es así, la variación en la entropía será independiente de la trayectoria, y por lo tanto, a pesar de que el proceso sea irreversible, podremos elegir cualquier trayectoria reversible que permita hacer el mismo proceso entre los estados de equilibrio inicial y final.
Recordemos que para que un sistema se encuentre en equilibrio termodinámico, es necesario alcanzar los equilibrios mecánico, químico y térmico. Cualquier proceso irreversible supondrá apartarse de alguno de estos tipos de equilibrio, y por lo tanto, no cumplir con el equilibrio termodinámico. Como consecuencia de esto, se producirá un proceso que permita alcanzar nuevamente el equilibrio termodinámico perdido.
Podemos entonces calcular la variación en la entropía que se produce cuando el sistema ha sido irreversiblemente apartado del equilibrio termodinámico por alteración de alguno de los equilibrios particulares. En todos los casos consideraremos un recinto aislado que contiene al sistema y al ambiente, y a su vez consideraremos que el ambiente se comporta como un foco calorífico, es decir, que es capaz de recibir o entregar calor sin cambiar apreciablemente su temperatura. Veamos tres ejemplos de irreversibilidades
Procesos producidos por irreversibilidad mecánica externa
Se llama entropía generada mecánica externa, a la entropía generada por las irreversibilidades entre el sistema y el entorno provocadas por la realización de un trabajo. Supongamos que agitamos un líquido viscoso (sistema) que se encuentra en contacto con un foco calorífico a una temperatura T. La agitación implica la realización de trabajo W desde el ambiente hacia el sistema, pero como el sistema se encuentra en contacto con un foco calorífico, su temperatura no cambia. Esto implica que la energía absorbida por el sistema en forma de trabajo es devuelta al ambiente en forma de calor Q. Por lo tanto, en esta situación tenemos que:
1. El sistema absorbe una cantidad de trabajo W y cede una cantidad de calor Q tal que W = Q, en virtud de que, al estar rodeado de un foco calorífico, no puede cambiar su temperatura.
2. Como el sistema entrega toda la energía que absorbe, las propiedades termodinámicas del mismo no cambian, por lo tanto, el estado inicial y el estado final del sistema son iguales. Como consecuencia de esto, ΔSsis = 0.
3. El ambiente recibe una cantidad Q de calor del sistema a la temperatura T, por lo que ΔSamb > 0.
4. Finalmente, ΔSuniv > 0.
El caso analizado corresponde a una disipación isotérmica de trabajo en un sistema, el cual permanece invariable.
Ahora consideremos la agitación del mismo líquido viscoso pero esta vez dentro de un recipiente adiabático. En este caso, el ambiente y el sistema no pueden intercambiar calor, por lo que el trabajo W recibido por el sistema producirá un incremento de su energía interna, con el consecuente aumento de su temperatura. La entropía del ambiente permanece constante, pues el mismo no puede recibir ni ceder calor al sistema, es decir, ΔSamb = 0. Para calcular la variación en la entropía del sistema, partimos de la definición:
![]()
para la cual hemos sustituido el proceso irreversible en estudio por otro reversible que lleve al sistema desde el mismo estado inicial al final. Si consideramos que el proceso se lleva a cabo a presión constante, podemos reemplazar el trabajo realizado irreversiblemente por una transferencia reversible e isobárica de calor
![]()
donde hemos supuesto que CP es constante en el intervalo de temperatura considerado. Como T2 > T1, se deduce que ΔSsis > 0. Finalmente, se concluye que ΔSuniv > 0. Este caso analizado corresponde a una disipación adiabática de trabajo que conduce a un aumento en la energía interna.
Procesos producidos por irreversibilidad mecánica interna
Se llama entropía generada interna a la entropía generada por irreversibilidades internas al sistema. Estas irreversibilidades pueden ser rozamientos internos, diferencias de temperaturas o presión entre puntos del sistema, fenómenos de histéresis, difusión, reacciones químicas, etc. Consideremos un gas perfecto que se encuentra encerrado en un globo, y que el ambiente es el vacío.
Cuando se abre el globo, el gas tenderá a ocupar todo el espacio posible, produciéndose una expansión libre contra el vacío. El ΔSamb= 0, pues el sistema entrega trabajo con el ambiente y no calor. Para calcular la variación en la entropía del sistema, nuevamente partimos de la definición general:
![]()
donde hemos sustituido la trayectoria irreversible por alguna trayectoria reversible adecuada. En este caso, podemos considerar como trayectoria la expansión isotérmica de un gas perfecto.
Vale recordar que como la temperatura del sistema no cambia, ΔU = 0, y por lo tanto, Q = -W
Entonces,
![]()
como V2> V1, ΔSsis > 0, y finalmente, ΔSuniv > 0.
Procesos producidos por irreversibilidad térmica externa
Se llama entropía generada térmica externa, a la entropía generada por las irreversibilidades entre el sistema y el entorno provocadas por la transmisión de calor con un gradiente de temperatura. Este tipo de proceso incluye a aquellos que suponen una transferencia de calor en virtud de una diferencia finita de temperatura, como ocurre al poner en contacto dos cuerpos a diferentes temperaturas. Consideremos la transferencia de Q unidades de calor desde un sistema a T1 al ambiente, más frío, a T2 (T2 < T1). Las variaciones de entropía asociadas son:
![]()
como T2 < T1, ΔSuniv > 0.
Como conclusión general, los procesos reversibles tienen asociados un cambio de entropía del universo nulo, mientras que los procesos irreversibles están siempre asociados a un cambio en la entropía del universo positiva.
Desde otro punto de vista, al ingeniero lo que le interesa es reducir al máximo las irreversibilidades, ya que estas son las que limitan el rendimiento de las máquinas térmicas.